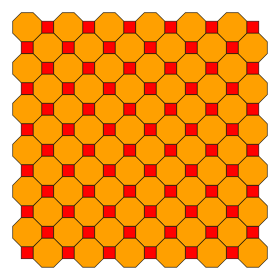
Усечённая квадратная мозаика
 Из Википедии, бесплатной энциклопедии
Из Википедии, бесплатной энциклопедии
| Усечённая квадратная мозаика | |
|---|---|
 | |
| Тип | Полуправильная мозаика |
| Конфигурация вершины |  4.8.8]] 4.8.8]] |
| Символ Шлефли | t{4,4} tr{4,4} или |
| Символ Витхоффа | 2 | 4 4 4 4 2 | |
| Симметрии | p4m, [4,4], (*442) |
| Симметрии вращения | p4, [4,4]+, (442) |
| Диаграммы Коксетера — Дынкина | |
| Группа Коксетера | H4, [5,3,3,3] |
| Двойственные соты | Разделённая квадратная мозаика |
| Свойства | Изогональные соты |
Усечённая квадратная мозаика — полуправильная мозаика из правильных многоугольников на евклидовой плоскости с одним квадратом и двумя восьмиугольниками в каждой вершине. Это единственная мозаика из правильных выпуклых многоугольников, содержащая соприкасающиеся сторонами восьмиугольники. Символ Шлефли мозаики равен t{4,4}.
Конвей называл эти мозаики «truncated quadrille» (усечённая кадриль), поскольку она строится на основе операции усечения на квадратном паркете (кадрили).
Другие названия для этой схемы — средиземноморская мозаика и восьмиугольная мозаика, которые часто используют меньшие квадраты, а восьмиугольники имеют перемежающиеся длинные и короткие стороны.
На плоскости существует 3 правильных и 8 полуправильных мозаик.
Однородные раскраски[править | править код]
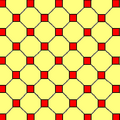
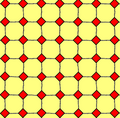
Существует две различные однородные раскраски усечённой квадратной мозаики. (Названия раскрасок по индексам цветов вокруг вершины (4.8.8): 122, 123.)
 2 цвета: 122 |  3 цвета: 123 |
Упаковка кругов[править | править код]
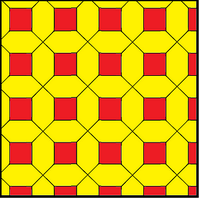
Мозаика из усечённых квадратов может быть использована для упаковки кругов, если разместить круги одинакового диаметра с центрами в вершинах мозаики. Каждый круг касается 3 других кругов в упаковке (контактное число)[1]. Поскольку все многоугольники имеют чётное число сторон, круги можно раскрасить альтернативным образом, как показано на втором рисунке.
Варианты[править | править код]
Вариант мозаики, часто называемой средиземноморской мозаикой, состоит из более мелких квадратных плиток, расположенных диагонально относительно границ. Другие варианты содержат растянутые квадраты или восьмиугольники.
Пифагорова мозаика перемежает большие и маленькие квадраты и топологически эквивалентна усечённой квадратной мозаике. В ней квадраты повёрнуты на 45 градусов, а восьмиугольники преобразованы в квадраты с вершинами в середине сторон.
Плетёная мозаика тоже имеет ту же топологию, что и усечённая квадратная мозаика со сплющенными в прямоугольники восьмиугольниками.
| p4m, (*442) | pmm (*2222) | p4g, (4*2) | cmm, (2*22) | |||
|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |
| p4m, (*442) | pmm (*2222) | p4, (442) | p4g, (4*2) | cmm, (2*22) | ||
 |  |  |  |  |  |  |
| Средиземноморская мозаика | Вытянутая мозаика | Пифагорова мозаика | Плетения | |||
Голландская кладка имеет ту же топологическую структуру со сплющенными в прямоугольники восьмиугольниками:
Связанные многогранники и мозаики[править | править код]
Усечённая квадратная мозаика (топологически) является частью последовательности однородных многогранников и мозаик с вершинными фигурами 4.2n.2n:
| *n42 мутации симметрий усечённых мозаик: 4.2n.2n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия *n42 [n,4] | Сферическая | Евклидова | Компактная гиперболическая | Паракомпактная. | |||||||
| *242 [2,4] | *342 [3,4] | *442 [4,4] | *542 [5,4] | *642 [6,4] | *742 [7,4] | *842 [8,4]... | *∞42 [∞,4] | ||||
| Усечённые фигуры |  |  |  |  |  |  |  |  | |||
| Конф. | 4.4.4 | 4.6.6 | 4.8.8 | 4.10.10 | 4.12.12 | 4.14.14 | 4.16.16 | 4.∞.∞ | |||
| n-kis figures |  |  |  |  |  |  |  |  | |||
| Конф. | V4.4.4 | V4.6.6 | V4.8.8 | V4.10.10 | V4.12.12 | V4.14.14 | V4.16.16 | V4.∞.∞ | |||
3-мерные биусечённые кубические соты, спроектированные в плоскость дают две копии усечённой мозаики. На плоскости соты могут быть представлена как составная мозаика, а комбинацию можно рассматривать как квадратную мозаику со снятой фаской.
 |  |  |
Построение Витхоффа из квадратной мозаики[править | править код]
Если раскрасить исходные грани квадратной мозаики красным цветом, жёлтым цветом плитки на месте вершин и синим цветом плитки на месте исходных сторон, все 8 форм будут различными. Однако, если рассматривать грани одинаково (как раскрашенные одним цветом), существует только три уникальные топологические формы: квадратная мозаика, усечённая квадратная мозаика, плосконосая квадратная мозаика.
| Однородные мозаики на основе симметрии квадратной мозаики | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [4,4], (*442) | [4,4]+, (442) | [4,4+], (4*2) | |||||||||
 |  |  |  |  |  |  |  | ||||
| {4,4} | t{4,4} | r{4,4} | t{4,4} | {4,4} | rr{4,4} | tr{4,4} | sr{4,4} | s{4,4} | |||
| Uniform duals | |||||||||||
 |  |  |  |  |  |  |  | ||||
| V4.4.4.4 | V4.8.8 | V4.4.4.4 | V4.8.8 | V4.4.4.4 | V4.4.4.4 | V4.8.8 | V3.3.4.3.4 | ||||
Связанные мозаики в других симметриях[править | править код]
| Симметрия *n42 [n,4] | Сферическая | Евклидова | Компактная гиперболическая | Паракомп. | ||||
|---|---|---|---|---|---|---|---|---|
| *242 [2,4] | *342 [3,4] | *442 [4,4] | *542 [5,4] | *642 [6,4] | *742 [7,4] | *842 [8,4]… | *∞42 [∞,4] | |
| Общеусечённая фигура |  4.8.4 |  4.8.6 |  4.8.8 |  4.8.10 |  4.8.12 |  4.8.14 |  4.8.16 |  4.8.∞ |
| Общеусечённые двойственные |  V4.8.4 |  V4.8.6 |  V4.8.8 |  V4.8.10 |  V4.8.12 |  V4.8.14 |  V4.8.16 |  V4.8.∞ |
| *nn2 мутации симметрий всеусечённых мозаик: 4.2n.2n | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия *nn2 [n,n] | Сферическая | Евклидова | Компактная гиперболическая | Паракомпактная | ||||||||||
| *222 [2,2] | *332 [3,3] | *442 [4,4] | *552 [5,5] | *662 [6,6] | *772 [7,7] | *882 [8,8]... | *∞∞2 [∞,∞] | |||||||
| Рисунок |  |  |  |  |  |  |  |  | ||||||
| Конф. | 4.4.4 | 4.6.6 | 4.8.8 | 4.10.10 | 4.12.12 | 4.14.14 | 4.16.16 | 4.∞.∞ | ||||||
| Двойственная фигура |  |  |  |  |  |  |  |  | ||||||
| Конф. | V4.4.4 | V4.6.6 | V4.8.8 | V4.10.10 | V4.12.12 | V4.14.14 | V4.16.16 | V4.∞.∞ | ||||||
Разделённая квадратная мозаика[править | править код]

Разделённая квадратная мозаика — мозаика евклидовой плоскости, двойственная усечённой квадратной мозаике. Она может быть построена, исходя из квадратной мозаики путём деления каждого квадрата на четыре равнобедренных прямоугольных треугольника, образуя бесконечную конфигурацию прямых. Эту же мозаику можно получить из квадратной мозаики путём деления каждого квадрата на два треугольника по диагонали, меняя попеременно направление диагоналей. Можно получить мозаику наложением двух квадратных решёток, одна из которых повёрнута на 45 градусов относительно другой и увеличена на множитель √2.
Конвей называл эту мозаику «kisquadrille» = «kis + quadrille»[2], где kis — операция, которая добавляет центральную точку и треугольники и заменяет тем самым грани квадратной мозаики («quadrille»). Мозаика также иногда называется решёткой Union Jack ввиду сходства с флагом Великобритании[3].
См. также[править | править код]
- Мозаики из выпуклых правильных многоугольников на евклидовой плоскости
- Список однородных мозаик
- Порог просачивания
Примечания[править | править код]
- ↑ Critchlow, 1987, с. 74-75.
- ↑ Conway, Burgiel, Goodman-Strass, 2008, с. 288 table.
- ↑ Stephenson, 1970, с. 4405–4409.
Литература[править | править код]
- Keith Critchlow. circle pattern H // Order in Space: A design source book. — New York: Thames & Hudson Inc., 1987. — ISBN 0-500-34033-1.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. The Symmetries of Things. — Wellesley, MA: A K Peters, Ltd., 2008. — ISBN 978-1-56881-220-5.
- John Stephenson. Ising Model with Antiferromagnetic Next-Nearest-Neighbor Coupling: Spin Correlations and Disorder Points // Phys. Rev. B. — 1970. — Т. 1, вып. 11. — doi:10.1103/PhysRevB.1.4405.
- Branko Grünbaum, G. C. Shephard. Chapter 2.1: Regular and uniform tilings // Tilings and Patterns. — New York: W. H. Freeman, 1987. — С. 58—65. — ISBN 0-7167-1193-1.
- Robert Williams. The Geometrical Foundation of Natural Structure. — New York: Dover Publications, 1979. — ISBN 048623729X.
- Dale Seymour, Jill Britton. Introduction to Tessellations. — Palo Alto: Dale Seymour Publications, 1989. — С. 50—56. — ISBN 978-0866514613.
Ссылки[править | править код]
- http://www.decrete.com/stencils/octagontile
- Weisstein, Eric W. Semiregular tessellation (англ.) на сайте Wolfram MathWorld.
- Klitzing, Richard. 2D Euclidean tilings o4x4x — tosquat — O6
Для улучшения этой статьи желательно:
|



