| Гіперплощина |
 |
| Формула |   |
|---|
| Підтримується Вікіпроєктом | Вікіпедія:Проєкт:Математика  |
|---|
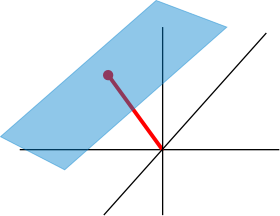
Гіперплощина — підпростір евклідового або афінного простору корозмірності 1, тобто із розмірністю, на одиницю меншою, ніж об'ємний простір.
Наприклад, для двовимірного простору гіперплощиною є пряма, для тривимірного — площина тощо.
Нехай  — нормальний вектор до гіперплощини, тоді рівняння гіперплощини, що проходить через точку
— нормальний вектор до гіперплощини, тоді рівняння гіперплощини, що проходить через точку  , має вигляд
, має вигляд

Тут  — скалярний добуток в просторі
— скалярний добуток в просторі  . В частковому випадку рівняння приймає вигляд
. В частковому випадку рівняння приймає вигляд

Нехай  — нормальний вектор до гіперплощини, тоді відстань від точки
— нормальний вектор до гіперплощини, тоді відстань від точки  до цієї гіперплощини задається формулою
до цієї гіперплощини задається формулою

де  — довільна точка гіперплощини.
— довільна точка гіперплощини.












