바닥 함수와 천장 함수

수학과 컴퓨터 과학에서 바닥 함수(영어: floor function)는 각 실수 이하의 최대 정수를 구하는 함수이다. 천장 함수(天障函數, 영어: ceiling function)는 각 실수 이상의 최소 정수를 구하는 함수이다. 바닥 함수는 내림 함수 · 버림 함수 · 최대 정수 함수(最大整數函數, 영어: greatest integer function)라고도 하며, 천장 함수는 올림 함수 · 최소 정수 함수(最小整數函數, 영어: least integer function)라고도 한다.

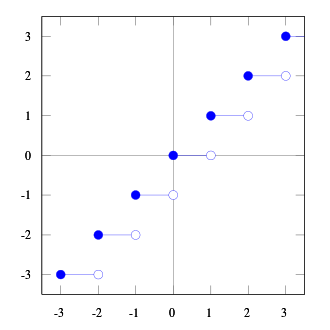
바닥 함수 ${\displaystyle \lfloor -\rfloor \colon \mathbb {R} \to \mathbb {Z} }$는 다음과 같다.

${\displaystyle \lfloor x\rfloor =\max\{n\in \mathbb {Z} \colon n\leq x\}}$

즉, 실수 ${\displaystyle x}$의 바닥 함수 값은 ${\displaystyle x}$와 같거나 그보다 작은 정수 가운데 가장 큰 하나이다. 예를 들어, 다음과 같다.

${\displaystyle \lfloor 5.2\rfloor =5}$

${\displaystyle \lfloor -5.2\rfloor =-6}$

${\displaystyle \lfloor 3\rfloor =3}$

${\displaystyle \lfloor -4\rfloor =-4}$

바닥 함수의 여러 가지 표기법은 다음과 같다.

• ${\displaystyle \lfloor x\rfloor }$
• ${\displaystyle [x]}$ 이를 가우스 기호라고 한다. 하지만 바닥 함수는 가우스 함수와 관련이 없다.
• ${\displaystyle \operatorname {floor} (x)}$

마찬가지로, 천장 함수 ${\displaystyle \lceil -\rceil \colon \mathbb {R} \to \mathbb {Z} }$는 다음과 같다.

${\displaystyle \lceil x\rceil =\min\{n\in \mathbb {Z} \colon n\geq x\}}$

즉, 실수 ${\displaystyle x}$의 천장 함수 값은 ${\displaystyle x}$와 같거나 그보다 큰 정수 가운데 가장 작은 하나이다. 예를 들어, 다음과 같다.

${\displaystyle \lceil 3.72\rceil =4}$

${\displaystyle \lceil -3.72\rceil =-3}$

${\displaystyle \lceil 4\rceil =4}$

${\displaystyle \lceil -2\rceil =-2}$

천장 함수의 여러 가지 표기법은 다음과 같다.

• ${\displaystyle \lceil x\rceil }$
• ${\displaystyle \operatorname {ceil} (x)}$

분수 부분 함수(分數部分函數, 영어: fractional part function) ${\displaystyle \{-\}\colon \mathbb {R} \to [0,1)}$는 다음과 같다.

${\displaystyle \{x\}=x-\lfloor x\rfloor =\min\{y\in \mathbb {R} _{\geq 0}\colon x-y\in \mathbb {Z} \}}$

예를 들어, 다음과 같다.

${\displaystyle \{8.21\}=0.21}$

${\displaystyle \{-8.21\}=0.79}$

${\displaystyle \{5\}=0}$

${\displaystyle \{-7\}=0}$

분수 부분 함수의 여러 가지 표기법은 다음과 같다.

• ${\displaystyle \{x\}}$
• ${\displaystyle \operatorname {frac} (x)}$

다음과 같은 부등식들이 성립한다.

${\displaystyle \lfloor x\rfloor \leq x<\lfloor x\rfloor +1}$

${\displaystyle \lceil x\rceil -1<x\leq \lceil x\rceil }$

비슷하게, 다음과 같은 부등식들이 성립한다.

${\displaystyle x-1<\lfloor x\rfloor \leq x}$

${\displaystyle x\leq \lceil x\rceil <x+1}$

${\displaystyle 0\leq \{x\}<1}$

삼각 부등식과 닮은 다음과 같은 부등식들이 성립한다.

${\displaystyle \lfloor x\rfloor +\lfloor y\rfloor \leq \lfloor x+y\rfloor \leq \lfloor x\rfloor +\lfloor y\rfloor +1}$

${\displaystyle \lceil x\rceil +\lceil y\rceil -1\leq \lceil x+y\rceil \leq \lceil x\rceil +\lceil y\rceil }$

바닥 함수와 천장 함수를 통해 실수 부등식과 동치인 정수 부등식을 얻을 수 있다. 즉, 임의의 ${\displaystyle n\in \mathbb {Z} }$ 및 ${\displaystyle x\in \mathbb {R} }$에 대하여, 다음 두 부등식이 서로 동치이다.

• ${\displaystyle n>x}$
• ${\displaystyle n>\lfloor x\rfloor }$

마찬가지로, ${\displaystyle n}$ 및 ${\displaystyle x}$에 대하여, 다음 두 부등식이 서로 동치이다.

• ${\displaystyle n<x}$
• ${\displaystyle n<\lceil x\rceil }$

마찬가지로, ${\displaystyle n}$ 및 ${\displaystyle x}$에 대하여, 다음 두 부등식이 서로 동치이다.

• ${\displaystyle n\geq x}$
• ${\displaystyle n\geq \lceil x\rceil }$

마찬가지로, ${\displaystyle n}$ 및 ${\displaystyle x}$에 대하여, 다음 두 부등식이 서로 동치이다.

• ${\displaystyle n\leq x}$
• ${\displaystyle n\leq \lfloor x\rfloor }$

천장 함수를 다음과 같이 바닥 함수를 써서 나타낼 수 있다.

${\displaystyle \lceil x\rceil =-\lfloor -x\rfloor ={\begin{cases}\lfloor x\rfloor &x\in \mathbb {Z} \\\lfloor x\rfloor +1&x\not \in \mathbb {Z} \end{cases}}}$

비슷하게, 다음과 같은 항등식들이 성립한다.

${\displaystyle \lfloor -x\rfloor ={\begin{cases}-\lfloor x\rfloor &x\in \mathbb {Z} \\-\lfloor x\rfloor -1&x\not \in \mathbb {Z} \end{cases}}}$

${\displaystyle \lceil -x\rceil ={\begin{cases}-\lceil x\rceil &x\in \mathbb {Z} \\-\lceil x\rceil +1&x\not \in \mathbb {Z} \end{cases}}}$

${\displaystyle \{-x\}={\begin{cases}0&x\in \mathbb {Z} \\-\{x\}+1&x\not \in \mathbb {Z} \end{cases}}}$

임의의 정수는 바닥 함수와 천장 함수의 고정점이다.

${\displaystyle \lfloor n\rfloor =\lceil n\rceil =n\qquad n\in \mathbb {Z} }$

바닥 함수와 천장 함수의 정의에 따라, 다음과 같은 항등식들이 성립한다.

${\displaystyle \max\{n\in \mathbb {Z} \colon n\leq x\}=\lfloor x\rfloor }$

${\displaystyle \min\{n\in \mathbb {Z} \colon n\geq x\}=\lceil x\rceil }$

${\displaystyle \min\{n\in \mathbb {Z} \colon n>x\}=\lfloor x\rfloor +1}$

${\displaystyle \max\{n\in \mathbb {Z} \colon n<x\}=\lceil x\rceil -1}$

바닥 함수와 천장 함수와 분수 부분 함수의 합성은 다음과 같다. 특히, 바닥 함수와 천장 함수와 분수 부분 함수는 모두 멱등 함수이다.

${\displaystyle \lfloor \lfloor x\rfloor \rfloor =\lfloor x\rfloor }$

${\displaystyle \lceil \lceil x\rceil \rceil =\lceil x\rceil }$

${\displaystyle \{\{x\}\}=\{x\}}$

${\displaystyle \lceil \lfloor x\rfloor \rceil =\lfloor x\rfloor }$

${\displaystyle \lfloor \lceil x\rceil \rfloor =\lceil x\rceil }$

${\displaystyle \{\lfloor x\rfloor \}=0}$

${\displaystyle \lfloor \{x\}\rfloor =0}$

${\displaystyle \{\lceil x\rceil \}=0}$

${\displaystyle \lceil \{x\}\rceil ={\begin{cases}0&x\in \mathbb {Z} \\1&x\not \in \mathbb {Z} \end{cases}}}$

임의의 ${\displaystyle n\in \mathbb {Z} }$ 및 ${\displaystyle x\in \mathbb {R} }$에 대하여, 다음과 같은 항등식들이 성립한다. 특히, 분수 부분 함수는 양의 최소 주기가 1인 주기 함수이다.

${\displaystyle \lfloor x+n\rfloor =\lfloor x\rfloor +n}$

${\displaystyle \lceil x+n\rceil =\lceil x\rceil +n}$

${\displaystyle \{x+n\}=\{x\}}$

임의의 ${\displaystyle m,n\in \mathbb {Z} }$ (${\displaystyle n>0}$) 및 ${\displaystyle x\in \mathbb {R} }$에 대하여, 다음과 같은 항등식들이 성립한다.

${\displaystyle \left\lfloor {\frac {x+m}{n}}\right\rfloor =\left\lfloor {\frac {\lfloor x\rfloor +m}{n}}\right\rfloor }$

${\displaystyle \left\lceil {\frac {x+m}{n}}\right\rceil =\left\lceil {\frac {\lceil x\rceil +m}{n}}\right\rceil }$

${\displaystyle {\biggl \lceil }{\frac {m}{n}}{\biggr \rceil }=\left\lfloor {\frac {m+n-1}{n}}\right\rfloor }$

임의의 ${\displaystyle n\in \mathbb {Z} ^{+}}$ 및 ${\displaystyle x,y\in \mathbb {R} }$에 대하여, 다음과 같은 항등식들이 성립한다.

${\displaystyle \lfloor \lfloor x/y\rfloor /n\rfloor =\lfloor x/(yn)\rfloor }$

${\displaystyle \lceil \lceil x/y\rceil /n\rceil =\lceil x/(yn)\rceil }$

임의의 ${\displaystyle n\in \mathbb {Z} ^{+}}$ 및 ${\displaystyle x\in \mathbb {R} }$에 대하여, 다음과 같은 합 공식이 성립한다. 이를 에르미트 항등식이라고 한다.

${\displaystyle \lfloor nx\rfloor =\lfloor x\rfloor +\left\lfloor x+{\frac {1}{n}}\right\rfloor +\cdots +\left\lfloor x+{\frac {n-1}{n}}\right\rfloor }$

${\displaystyle \lceil nx\rceil =\lceil x\rceil +\left\lceil x-{\frac {1}{n}}\right\rceil +\cdots +\left\lceil x-{\frac {n-1}{n}}\right\rceil }$

특히, ${\displaystyle x=m/n}$ (${\displaystyle m\in \mathbb {Z} }$)인 경우 다음과 같다.

${\displaystyle {\begin{aligned}m&={\biggl \lfloor }{\frac {m}{n}}{\biggr \rfloor }+\left\lfloor {\frac {m+1}{n}}\right\rfloor +\cdots +\left\lfloor {\frac {m+n-1}{n}}\right\rfloor \\&={\biggl \lceil }{\frac {m}{n}}{\biggr \rceil }+\left\lceil {\frac {m-1}{n}}\right\rceil +\cdots +\left\lceil {\frac {m-n+1}{n}}\right\rceil \end{aligned}}}$

특히, ${\displaystyle n=2}$인 경우 다음과 같은 항등식을 유도할 수 있다.

${\displaystyle m={\biggl \lfloor }{\frac {m}{2}}{\biggr \rfloor }+{\biggl \lceil }{\frac {m}{2}}{\biggr \rceil }}$

임의의 ${\displaystyle m,n\in \mathbb {Z} ^{+}}$ 및 ${\displaystyle x\in \mathbb {R} }$에 대하여, 다음이 성립한다.

${\displaystyle {\biggl \lfloor }{\frac {x}{n}}{\biggr \rfloor }+{\biggl \lfloor }{\frac {x+m}{n}}{\biggr \rfloor }+\left\lfloor {\frac {x+2m}{n}}\right\rfloor +\cdots +\left\lfloor {\frac {x+(n-1)m}{n}}\right\rfloor ={\biggl \lfloor }{\frac {x}{m}}{\biggr \rfloor }+{\biggl \lfloor }{\frac {x+n}{m}}{\biggr \rfloor }+\left\lfloor {\frac {x+2n}{m}}\right\rfloor +\cdots +\left\lfloor {\frac {x+(m-1)n}{m}}\right\rfloor }$

즉, 이러한 합 공식은 ${\displaystyle m,n}$의 순서와 무관하다. 특히, ${\displaystyle x=0}$인 경우 합이 다음과 같이 주어진다.

${\displaystyle {\biggl \lfloor }{\frac {m}{n}}{\biggr \rfloor }+\left\lfloor {\frac {2m}{n}}\right\rfloor +\cdots +\left\lfloor {\frac {(n-2)m}{n}}\right\rfloor ={\frac {(m-1)(n-1)+\gcd\{m,n\}-1}{2}}}$

특히, ${\displaystyle m,n}$이 서로소인 경우 (즉, ${\displaystyle \gcd\{m,n\}=1}$인 경우) 다음과 같다.

${\displaystyle {\biggl \lfloor }{\frac {m}{n}}{\biggr \rfloor }+\left\lfloor {\frac {2m}{n}}\right\rfloor +\cdots +\left\lfloor {\frac {(n-2)m}{n}}\right\rfloor ={\frac {(m-1)(n-1)}{2}}}$

분수 부분 함수는 1-주기 함수이며, 그 푸리에 급수는 다음과 같다.

${\displaystyle \{x\}={\frac {1}{2}}-{\frac {1}{\pi }}\sum _{n=1}^{\infty }{\frac {\sin(2n\pi x)}{n}}\qquad x\not \in \mathbb {Z} }$

바닥 함수와 천장 함수는 주기 함수가 아니므로, 이들의 푸리에 급수는 균등 수렴하지 않는다. 바닥 함수와 천장 함수는 조각마다 일차 함수이며, 분수 부분 함수는 조각마다 상수 함수이다. 이 셋의 불연속점 집합은 모두 정수 집합이다.

실수 ${\displaystyle x}$의 정수 부분은 ${\displaystyle \lfloor x\rfloor }$이며, 분수 부분은 ${\displaystyle \{x\}}$이다. 분수 부분은 소수 부분이라 하기도 한다. 예를 들어, 다음과 같다.

${\displaystyle \lfloor 2.34\rfloor =2}$

${\displaystyle \{2.34\}=0.34}$

컴퓨터 과학에서는 정수 부분과 분수 부분을 조금 다르게 정의하기도 한다. 예를 들어, 다음과 같은 변형된 정수 부분 함수와 분수 부분 함수가 쓰인다.

${\displaystyle \operatorname {ip} (x):=\operatorname {sgn}(x)\lfloor |x|\rfloor ={\begin{cases}\lfloor x\rfloor &x\geq 0\\\lceil x\rceil &x<0\end{cases}}}$

${\displaystyle \operatorname {fp} (x):=x-\operatorname {ip} (x)=\operatorname {sgn}(x)(|x|-\lfloor |x|\rfloor )={\begin{cases}x-\lfloor x\rfloor &x\geq 0\\x-\lceil x\rceil &x<0\end{cases}}}$

 이 부분의 본문은 올림과 버림입니다.

실수 ${\displaystyle x}$를 정수로 내림한 값은 ${\displaystyle \lfloor x\rfloor }$이며, 정수로 올림한 값은 ${\displaystyle \lceil x\rceil }$이다. 컴퓨터 과학에서는 변형된 내림·올림이 쓰이기도 한다. 즉, 실수 ${\displaystyle x}$를 정수로 내림(올림)한 값을 ${\displaystyle \operatorname {ip} (x)}$로 정의한다.

실수 ${\displaystyle x}$를 정수로 반올림한 값은 ${\displaystyle \lfloor x+0.5\rfloor }$이다. 예를 들어, 다음과 같다.

${\displaystyle \lfloor 2.34+0.5\rfloor =2}$

${\displaystyle \lfloor 7.5+0.5\rfloor =8}$

컴퓨터 과학에서는 반올림의 여러 가지 변형이 사용되는데, 이들은 반정수의 경우를 달리 정의하며, 그 밖의 경우는 원래의 반올림과 일치한다. 원래의 반올림은 반정수를 비교적 큰 정수로 근사한다. 반정수를 비교적 작은 정수로 근사하는 반올림은 ${\displaystyle x\mapsto \lceil x-0.5\rceil }$이며, 반정수를 절댓값이 비교적 큰 정수로 근사하는 반올림은 ${\displaystyle x\mapsto \operatorname {sgn}(x)\lfloor |x|+0.5\rfloor }$이며, 반정수를 절댓값이 비교적 작은 정수로 근사하는 반올림은 ${\displaystyle x\mapsto \operatorname {sgn}(x)\lceil |x|-0.5\rceil }$이다. 또한, 최근 정수 함수(最近整數函數, 영어: nearest integer function)라고 불리는 다음과 같은 함수는 반정수를 짝수로 근사하는 반올림 함수이다.

${\displaystyle \operatorname {nint} (x)=\lfloor x\rceil :=\lfloor x-0.5\rfloor -\left\lfloor {\frac {x-0.5}{2}}\right\rfloor -\left\lfloor -{\frac {x-0.5}{2}}\right\rfloor ={\begin{cases}\lfloor x+0.5\rfloor &x\not \in 2\mathbb {Z} +0.5\\\lfloor x-0.5\rfloor &x\in 2\mathbb {Z} +0.5\end{cases}}}$

두 정수 ${\displaystyle m,n\in \mathbb {Z} }$ (${\displaystyle n\neq 0}$)의 나머지 있는 나눗셈의 결과를 바닥 함수를 통해 나타낼 수 있다. 즉, 몫은

${\displaystyle {\biggl \lfloor }{\frac {m}{n}}{\biggr \rfloor }}$

이며, 나머지는

${\displaystyle m-{\biggl \lfloor }{\frac {m}{n}}{\biggr \rfloor }n}$

이다.

${\displaystyle b}$진법에서 정수 ${\displaystyle n}$의 자릿수는

${\displaystyle \lfloor \log _{b}|n|\rfloor +1=\lceil \log _{b}(|n|+1)\rceil }$

이다.

양의 정수 ${\displaystyle n}$ 및 소수 ${\displaystyle p}$에 대하여, ${\displaystyle p^{e}\mid n!}$인 최대 ${\displaystyle e}$는

${\displaystyle \left\lfloor {\frac {n}{p}}\right\rfloor +\left\lfloor {\frac {n}{p^{2}}}\right\rfloor +\cdots +{\biggl \lfloor }{\frac {n}{p^{\lfloor \log _{p}n\rfloor }}}{\biggr \rfloor }}$

이다. 이를 르장드르 공식이라고 한다.

1808년에 카를 프리드리히 가우스는 이차 상호 법칙의 세 번째 증명에서 기호 ${\displaystyle [x]}$를 사용하여 바닥 함수를 정의하였다.^[1] 이 기호는 1962년에 케네스 아이버슨이 《프로그래밍 언어》(A Programming Language)라는 책에서 바닥 함수와 천장 함수라는 용어를 정의하고 기호로 각각 ${\displaystyle \lfloor x\rfloor }$와 ${\displaystyle \lceil x\rceil }$로 나타낼 때까지 표준 형태였다.^[2][3] 지금은 두 사람의 기호가 모두 쓰이고 있다.

• 수학 기호

위키미디어 공용에 바닥 함수와 천장 함수 주제와 관련된 미디어 분류가 있습니다.

• “Floor function”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4. 
• Weisstein, Eric Wolfgang. “Floor function”. 《Wolfram MathWorld》 (영어). Wolfram Research. 
• Weisstein, Eric Wolfgang. “Ceiling function”. 《Wolfram MathWorld》 (영어). Wolfram Research. 
• “Definition:Floor function”. 《ProofWiki》 (영어). 
• “Definition:Ceiling function”. 《ProofWiki》 (영어). 
• “Definition:Fractional part”. 《ProofWiki》 (영어).