노모그램

노모그램(nomogram) 또는 노모그래프, 얼라인먼트 차트, 아바크라고도 불리는 이 도구는 아날로그 계산 장치로, 수학적 함수의 근사적인 그래픽 계산을 가능하게 설계된 2차원 다이어그램이다. 노모그래피 분야는 1884년 프랑스 엔지니어 필베르 모리스 도카뉴가 발명했으며, 수십 년 동안 엔지니어들이 복잡한 공식의 빠르고 그래픽적인 계산을 실용적인 정확도로 제공하기 위해 광범위하게 사용되었다. 노모그램은 표준 직교 좌표계 대신 도카뉴가 발명한 평행 좌표계를 사용한다.

노모그램은 방정식의 각 변수에 대해 하나의 눈금이 있는 n개의 눈금으로 구성된다. n-1개 변수의 값을 알면 알 수 없는 변수의 값을 찾거나, 일부 변수의 값을 고정하여 고정되지 않은 변수 간의 관계를 연구할 수 있다. 결과는 눈금에 알려진 값에 직선자를 대고 해당 변수의 눈금을 가로지르는 지점에서 알 수 없는 값을 읽어 얻는다. 직선자에 의해 만들어진 가상 또는 그려진 선을 인덱스 선 또는 등치선이라고 한다.

노모그램은 포켓 계산기 시대 이전에 빠르고 정확한 계산을 가능하게 했기 때문에 약 75년 동안 다양한 맥락에서 번성했다. 노모그램의 결과는 하나 이상의 선을 그리는 것만으로 매우 빠르고 안정적으로 얻을 수 있다. 사용자는 대수 방정식을 푸는 방법, 표에서 데이터를 찾는 방법, 계산자를 사용하는 방법, 또는 결과에 대한 숫자를 방정식에 대입하는 방법을 알 필요가 없다. 사용자는 노모그램이 나타내는 기본 방정식조차 알 필요가 없다. 또한 노모그램은 설계에 암묵적이거나 명시적인 도메인 지식을 자연스럽게 통합한다. 예를 들어, 더 높은 정확도를 위해 더 큰 노모그램을 만들 때 노모그래머는 문제에 합리적이고 흥미로운 눈금 범위만 포함하는 경향이 있다. 많은 노모그램은 참조 레이블 및 색상 영역과 같은 다른 유용한 표시를 포함한다. 이러한 모든 기능은 사용자에게 유용한 안내를 제공한다.

계산자처럼 노모그램은 그래픽 아날로그 계산 장치이다. 또한 계산자와 마찬가지로 물리적 표시를 그리고 복제하고 보고 정렬하는 정확도에 의해 정확도가 제한된다. 일반적인 계산 장치인 계산자와 달리 노모그램은 장치의 눈금에 내장된 값 테이블을 사용하여 특정 계산을 수행하도록 설계되었다. 노모그램은 일반적으로 제공하는 정확도 수준이 충분하고 유용한 응용 프로그램에 사용된다. 또는 노모그램은 더 정확하지만 오류가 발생하기 쉬운 계산으로 얻은 답을 확인하는 데 사용할 수 있다.

교차 차트, 삼변 다이어그램, 육각형 차트와 같은 다른 종류의 그래픽 계산기는 때때로 노모그램이라고 불린다. 이 장치들은 하나 이상의 선형 등치선을 사용하여 해를 찾는 그래픽 계산기라는 노모그램의 정의를 충족하지 않는다.

세 변수 방정식에 대한 노모그램은 일반적으로 세 개의 눈금을 가지지만, 두 개 또는 세 개 모두 눈금이 공통인 노모그램도 존재한다. 여기에서 두 눈금은 알려진 값을 나타내고 세 번째 눈금은 결과를 읽는 눈금이다. 가장 간단한 방정식은 세 변수 u₁, u₂, u₃에 대한 u₁ + u₂ + u₃ = 0이다. 이 유형의 노모그램의 예가 오른쪽에 표시되어 있으며 노모그램의 부분을 설명하는 데 사용되는 용어로 주석이 달려 있다.

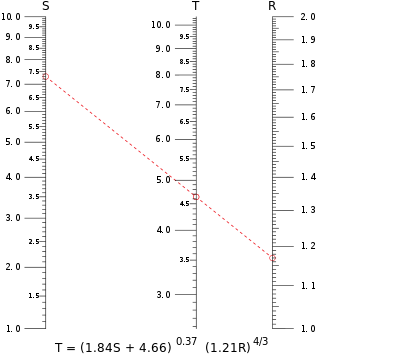
더 복잡한 방정식은 때때로 세 변수의 함수의 합으로 표현될 수 있다. 예를 들어, 이 문서 상단의 노모그램은 방정식 양변에 로그를 취한 후 그런 합으로 표현될 수 있기 때문에 평행 눈금 노모그램으로 구성될 수 있었다.

알려지지 않은 변수에 대한 눈금은 다른 두 눈금 사이에 있거나 외부에 있을 수 있다. 계산의 알려진 값은 해당 변수의 눈금에 표시되고, 이 표시들 사이에 선이 그려진다. 결과는 선이 해당 눈금과 교차하는 지점에서 알려지지 않은 눈금에서 읽는다. 눈금에는 정확한 숫자 위치를 나타내는 '눈금 표시'가 포함되어 있으며, 레이블이 지정된 참조 값이 포함될 수도 있다. 이러한 눈금은 선형, 로그 눈금, 또는 더 복잡한 관계를 가질 수 있다.

이 문서 상단에 있는 노모그램에 빨간색으로 표시된 샘플 등치선은 S = 7.30 및 R = 1.17일 때 T의 값을 계산한다. 등치선은 4.65 바로 아래에서 T의 눈금을 가로지른다. 고해상도로 용지에 인쇄된 더 큰 그림은 3자리 정밀도로 T = 4.64를 산출한다. 어떤 변수든 다른 두 변수의 값에서 계산될 수 있다는 점에 유의하라. 이는 대수적으로 다른 변수에서 변수를 분리할 수 없는 방정식에 특히 유용한 노모그램의 특징이다.

직선 눈금은 비교적 간단한 계산에 유용하지만, 더 복잡한 계산에는 간단하거나 정교한 곡선 눈금이 필요할 수 있다. 세 개 이상의 변수에 대한 노모그램은 두 변수에 대한 눈금 격자를 통합하거나, 더 적은 수의 변수에 대한 개별 노모그램을 연결하여 복합 노모그램으로 구성할 수 있다.

노모그램은 광범위한 응용 분야에서 사용되었다. 샘플에는 다음이 포함된다.

• 도카뉴의 원래 응용 분야인 프랑스 국영 철도 시스템 건설 중 토지 제거를 위한 복잡한 절토 및 성토 계산 자동화. 이 계산은 사소하지 않고 그 결과가 상당한 시간, 노력 및 비용 절감으로 이어졌기 때문에 중요한 개념 증명이었다.
• 물의 흐름 조절을 위한 수로, 파이프 및 전선 설계.
• 로렌스 헨더슨의 연구에서 노모그램은 혈액 생리학의 여러 측면을 상관시키는 데 사용되었다. 이는 미국에서 노모그램의 첫 번째 주요 사용이었고 전 세계 의학 노모그램 중에서도 처음이었다.
• 약학 및 종양학 등 의료 분야^[1]
• 사격 통제 시스템 이전의 탄도 계산. 여기서 계산 시간은 중요했다.
• 기계 공장 계산. 청사진 치수를 변환하고 재료 치수 및 속성에 기반한 계산을 수행한다. 이러한 노모그램에는 종종 표준 치수 및 사용 가능한 제조 부품에 대한 표시가 포함되었다.
• 통계학. 분포 특성의 복잡한 계산 및 품질 관리를 위한 합격 테스트 설계 등 운영 연구를 위한 통계학.
• 운영 연구. 다양한 최적화 문제에서 결과를 얻기 위해.
• 화학 및 화학 공학. 일반 물리적 관계 및 특정 화합물에 대한 경험적 데이터를 모두 캡슐화하기 위해.
• 항공학. 수십 년 동안 모든 종류의 항공기 조종석에서 노모그램이 사용되었다. 항법 및 비행 제어 보조 도구로서 노모그램은 빠르고 작고 사용하기 쉬운 계산기였다.
• 파벨 엘랴스베르크의 스푸트니크 1호 발사 후 궤도 계산과 같은 천문 계산.^[2]
• 모든 종류의 엔지니어링 작업: 필터 및 전송 라인의 전기 설계, 응력 및 하중의 기계 계산, 광학 계산 등.
• 군사. 복잡한 계산을 현장에서 빠르고 전기 장치에 의존하지 않고 안정적으로 수행해야 하는 군사.
• 지진학. 지진 규모를 추정하고 확률론적 지진 위험 분석 결과를 제시하기 위해 노모그램이 개발되었다.^[3]

아래 노모그램은 다음 계산을 수행한다.

$${\displaystyle f(A,B)={\frac {1}{1/A+1/B}}={\frac {AB}{A+B}}}$$

이 노모그램은 직선의 균일한 눈금만 사용하여 유용한 비선형 계산을 수행한다는 점에서 흥미롭다. 대각선 눈금은 축 눈금보다 ${\displaystyle {\sqrt {2}}}$배 크지만, 그 위에 있는 숫자는 바로 아래 또는 왼쪽에 있는 숫자와 정확히 일치하므로 모눈 종이에 대각선으로 직선을 그려 쉽게 만들 수 있다.

A와 B는 가로 및 세로 눈금에 입력하고, 결과는 대각선 눈금에서 읽는다. A와 B의 조화 평균에 비례하는 이 공식은 여러 응용 분야를 가진다. 예를 들어, 전자공학의 병렬 저항 공식이자 광학의 박막 렌즈 방정식이다.

이 예에서 빨간색 선은 56옴과 42옴의 병렬 저항이 24옴의 합성 저항을 가짐을 보여준다. 또한 렌즈에서 56cm 거리에 있는 물체가 초점거리가 24cm인 렌즈에 의해 42cm 거리에 실상을 형성함을 보여준다.

아래 노모그램은 친숙한 통계 검정인 피어슨의 카이 제곱 검정을 수행할 때 필요한 일부 값의 근사 계산을 수행하는 데 사용할 수 있다. 이 노모그램은 고르지 않은 간격의 눈금을 가진 곡선 눈금의 사용을 보여준다.

관련 식은 다음과 같다.

$${\displaystyle {\frac {(OBS-EXP)^{2}}{EXP}}}$$

상단의 눈금은 관측값의 다섯 가지 다른 범위인 A, B, C, D 및 E에서 공유된다. 관측값은 이러한 범위 중 하나에서 찾고, 해당 눈금에 사용된 눈금 표시는 그 바로 위에 있다. 그런 다음 예상값에 사용되는 곡선 눈금은 범위에 따라 선택된다. 예를 들어, 9의 관측값은 범위 A의 9 위에 있는 눈금 표시를 사용하고, 예상값에는 곡선 눈금 A를 사용한다. 81의 관측값은 범위 E의 81 위에 있는 눈금 표시를 사용하고, 예상값에는 곡선 눈금 E를 사용한다. 이를 통해 다섯 가지 다른 노모그램을 하나의 다이어그램에 통합할 수 있다.

이러한 방식으로 파란색 선은 다음 계산을 보여준다.

틀:In5 (9 − 5)² / 5 = 3.2

빨간색 선은 다음 계산을 보여준다.

틀:In5 (81 − 70)² / 70 = 1.7

검정을 수행할 때 종종 예이츠 연속성 수정이 적용되며, 이는 단순히 관측값에서 0.5를 빼는 것을 포함한다. 예이츠 수정으로 검정을 수행하기 위한 노모그램은 각 "관측" 눈금을 왼쪽으로 반 단위 이동하여 1.0, 2.0, 3.0, ... 눈금을 현재 차트에 0.5, 1.5, 2.5, ... 값이 나타나는 곳에 배치하여 간단히 구성할 수 있다.

노모그램은 수학적 관계를 나타내지만, 모두 수학적으로 도출된 것은 아니다. 다음 노모그램은 숫자가 아닌 주관적 단위의 관계의 곱으로 쉽게 정의할 수 있는 적절한 최종 결과를 얻기 위해 그래픽으로 개발되었다. 비평행 축의 사용은 비선형 관계를 모델에 통합할 수 있게 했다.

네모 상자 안의 숫자는 적절한 평가 후 입력을 요구하는 축을 나타낸다.

이미지 상단의 두 개의 노모그램은 발생 확률과 가용성을 결정하며, 이는 하단의 다단계 노모그램에 통합된다.

8번 및 10번 선은 '타이 선' 또는 '피벗 선'이며 복합 노모그램의 단계 간 전환에 사용된다.

평행 로그 눈금의 마지막 쌍(12)은 노모그램 자체는 아니지만, 위험 점수(11, 원격에서 매우 높음)를 안전 측면 및 기타 '소비자 보호' 측면에 대한 샘플링 빈도로 변환하기 위한 읽기 전용 눈금이다. 이 단계는 비용과 위험의 균형을 맞추는 정치적 '동의'가 필요하다. 이 예는 각각 3년 최소 빈도를 사용하지만, 두 측면에 대한 눈금의 고위험 끝이 다르므로 두 측면에 대해 다른 빈도를 제공하지만, 둘 다 최소 3년마다 모든 음식에 대해 모든 측면에서 최소 한 번은 전체 최소 샘플링을 받는다.

이 위험 평가 노모그램은 영국 식품기준청의 자금 지원을 받아 공공 분석가가 공식 식품 관리 목적을 위해 식품의 적절한 샘플링 및 분석 빈도를 안내하는 도구로 사용하기 위해 개발되었으며, 모든 음식의 모든 잠재적 문제를 평가하는 데 사용될 예정이지만 아직 채택되지 않았다.

자(ruler)를 사용하면 사인 법칙의 누락된 항이나 이차 방정식과 삼차 함수의 근을 쉽게 읽을 수 있다.^[4]

• 
  사인 법칙 노모그램
• 
  이차 방정식 x^2+px+q=0의 해를 구하는 노모그램
• 
  삼차 방정식 x^3+px+q=0의 해를 구하는 노모그램

• 카토그램
• 힐베르트의 13번째 문제
• 콜모고로프-아르놀트 표현 정리
• 부하선
• 로그-로그 그래프
• 반로그 그래프

• 위키미디어 공용에 노모그램 관련 미디어 분류가 있습니다.
• 노모그래피의 예술은 기하학, 행렬식, 변환을 사용하여 노모그램을 설계하는 방법을 설명한다.
• 노모그래피의 잊혀진 예술은 노모그래피 분야를 조사한 수학 저널 기사이다.
• 워게임용 노모그램이지만 일반적인 관심사도 있다.
• PyNomo – 노모그램 제작을 위한 오픈 소스 소프트웨어.
• 자바 애플릿 보관됨 2009-09-24 - 웨이백 머신 간단한 노모그램 제작을 위한 자바 애플릿.
• 세 변수 간의 관계 시각화를 위한 노모그램 - useR!2011에서 조나단 루지에르의 초청 강연 비디오 및 슬라이드.