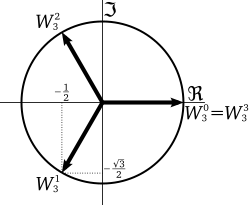
复平面上的立方根等於1. 棣莫弗公式 (英語:de Moivre's formula)是一個關於複數 和三角函數 的公式,命名自法國 數學家亞伯拉罕·棣美弗 (1667年-1754年)。其內容為對任意实数 x {\displaystyle x} 整數 n {\displaystyle n}
( cos ( x ) + i sin ( x ) ) n = cos ( n x ) + i sin ( n x ) {\displaystyle (\cos(x)+i\sin(x))^{n}=\cos(nx)+i\sin(nx)} 其中 i {\displaystyle i} 虛數單位 ( i 2 = − 1 {\displaystyle i^{2}=-1} [ 1] cos x + i sin x {\displaystyle \cos x+i\sin x} cis (x )
cis n ( x ) = cis ( n x ) {\displaystyle \operatorname {cis} ^{n}(x)=\operatorname {cis} (nx)} 在操作上,我們常常限制 x {\displaystyle x} 實數 ,這樣一來就可藉由比較虛部與實部的方式把 cos ( n x ) {\displaystyle \cos(nx)} sin ( n x ) {\displaystyle \sin(nx)} cos x {\displaystyle \cos x} sin x {\displaystyle \sin x} n {\displaystyle n} n {\displaystyle n}
(证明的思路是用数学归纳法 证明正整数的情形,并推广到负整数。)
令 P ( n ) = ( cos θ + i sin θ ) n = cos ( n θ ) + i sin ( n θ ) , n ∈ N {\displaystyle P(n)=(\cos \theta +i\sin \theta )^{n}=\cos(n\theta )+i\sin(n\theta ),n\in \mathbb {N} }
(1)当 n = 0 {\displaystyle n=0}
(2)當 n = 1 {\displaystyle n=1}
左式 = ( cos θ + i sin θ ) 1 = cos θ + i sin θ = cos ( 1 ⋅ θ ) + i sin ( 1 ⋅ θ ) = {\displaystyle =(\cos \theta +i\sin \theta )^{1}=\cos \theta +i\sin \theta =\cos(1\cdot \theta )+i\sin(1\cdot \theta )=}
因此, P ( 1 ) {\displaystyle P(1)}
(3)當 n > 1 {\displaystyle n>1}
假設 P ( k ) {\displaystyle P(k)} ( cos θ + i sin θ ) k = cos ( k θ ) + i sin ( k θ ) {\displaystyle (\cos \theta +i\sin \theta )^{k}=\cos(k\theta )+i\sin(k\theta )}
當 n = k + 1 {\displaystyle n=k+1}
( cos θ + i sin θ ) k + 1 = ( cos θ + i sin θ ) k ⋅ ( cos θ + i sin θ ) = ( cos k θ + i sin k θ ) ⋅ ( cos θ + i sin θ ) = ( cos k θ ⋅ cos θ + i sin k θ ⋅ i sin θ ) + ( cos k θ ⋅ i sin θ + i sin k θ ⋅ cos θ ) = ( cos k θ ⋅ cos θ − sin k θ ⋅ sin θ ) + i ( cos k θ ⋅ sin θ + sin k θ ⋅ cos θ ) = 1 cos ( k θ + θ ) + i sin ( k θ + θ ) = cos [ ( k + 1 ) θ ] + i sin [ ( k + 1 ) θ ] {\displaystyle {\begin{aligned}(\cos \theta +i\sin \theta )^{k+1}&=(\cos \theta +i\sin \theta )^{k}\cdot (\cos \theta +i\sin \theta )\\&=(\cos k\theta +i\sin k\theta )\cdot (\cos \theta +i\sin \theta )\\&=(\cos k\theta \cdot \cos \theta +i\sin k\theta \cdot i\sin \theta )+(\cos k\theta \cdot i\sin \theta +i\sin k\theta \cdot \cos \theta )\\&=(\cos k\theta \cdot \cos \theta -\sin k\theta \cdot \sin \theta )+i(\cos k\theta \cdot \sin \theta +\sin k\theta \cdot \cos \theta )\\&\ {\overset {1}{=}}\cos(k\theta +\theta )+i\sin(k\theta +\theta )\\&\ =\cos[(k+1)\theta ]+i\sin[(k+1)\theta ]\\\end{aligned}}}
等号1处使用和角公式 。
因此, P ( k + 1 ) {\displaystyle P(k+1)}
综上所述,根據數學歸納法, ∀ n ∈ N {\displaystyle \forall n\in \mathbb {N} } P ( n ) {\displaystyle P(n)}
另外,由恒等式:
( cos ( n θ ) + i sin ( n θ ) ) ⋅ ( cos ( − n θ ) + i sin ( − n θ ) ) = 1 {\displaystyle (\cos(n\theta )+i\sin(n\theta ))\cdot (\cos(-n\theta )+i\sin(-n\theta ))=1} 可知,公式对于负整数情况也成立。
证毕。
最简单的方法是应用欧拉公式 [ 2]
由於 e i x = cos x + i sin x {\displaystyle e^{ix}=\cos x+i\sin x\,} 所以 ( cos x + i sin x ) n = ( e i x ) n = e i n x = e i ( n x ) = cos ( n x ) + i sin ( n x ) {\displaystyle {\color {Green}(\cos x+i\sin x)^{n}}=(e^{ix})^{n}=e^{inx}=e^{i(nx)}={\color {Green}\cos(nx)+i\sin(nx)}} 此定理可用來求單位複數的 n {\displaystyle n} | z | = 1 {\displaystyle |z|=1}
z = cos θ + i sin θ {\displaystyle z=\cos \theta +i\sin \theta } 若 w n = z {\displaystyle w^{n}=z} w {\displaystyle w}
w = cos ϕ + i sin ϕ {\displaystyle w=\cos \phi +i\sin \phi } 按照棣莫弗公式:
w n = ( cos ϕ + i sin ϕ ) n = cos n ϕ + i sin n ϕ = cos θ + i sin θ = z {\displaystyle w^{n}=(\cos \phi +i\sin \phi )^{n}=\cos n\phi +i\sin n\phi =\cos \theta +i\sin \theta =z} 於是得到
n ϕ = θ + 2 k π {\displaystyle n\phi =\theta +2k\pi } k ∈ Z {\displaystyle k\in \mathbb {Z} } 也就是:
ϕ = θ + 2 k π n {\displaystyle \phi ={\dfrac {\theta +2k\pi }{n}}} 當 k {\displaystyle k} 0 , 1 , … , n − 1 {\displaystyle 0,1,\ldots ,n-1} n {\displaystyle n}
w = cos ( θ + 2 k π n ) + i sin ( θ + 2 k π n ) , k = 0 , 1 , … , n − 1 {\displaystyle w=\cos({\dfrac {\theta +2k\pi }{n}})+i\sin({\dfrac {\theta +2k\pi }{n}}),k=0,1,\ldots ,n-1} ^ Lial, Margaret L.; Hornsby, John; Schneider, David I.; Callie J., Daniels. College Algebra and Trigonometry 4th. Boston: Pearson/Addison Wesley. 2008: 792. ISBN 9780321497444 ^ 林琦焜. 棣美弗定理與 Euler 公式 (PDF) . 中央研究院 . 2006-12-22 [2017-06-18 ] . (原始内容存档 (PDF) 于2021-01-19). 




















![{\displaystyle {\begin{aligned}(\cos \theta +i\sin \theta )^{k+1}&=(\cos \theta +i\sin \theta )^{k}\cdot (\cos \theta +i\sin \theta )\\&=(\cos k\theta +i\sin k\theta )\cdot (\cos \theta +i\sin \theta )\\&=(\cos k\theta \cdot \cos \theta +i\sin k\theta \cdot i\sin \theta )+(\cos k\theta \cdot i\sin \theta +i\sin k\theta \cdot \cos \theta )\\&=(\cos k\theta \cdot \cos \theta -\sin k\theta \cdot \sin \theta )+i(\cos k\theta \cdot \sin \theta +\sin k\theta \cdot \cos \theta )\\&\ {\overset {1}{=}}\cos(k\theta +\theta )+i\sin(k\theta +\theta )\\&\ =\cos[(k+1)\theta ]+i\sin[(k+1)\theta ]\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21413d9f5c297b9f261a27ad0830a9db892c3257)

















