幾何學中,三維點群是三維空間中,任何一個固定原點的對稱群。等價的說法是,其為球面的對稱群。此類群皆為正交群 的子群,即固定原點的全體等距同構組成的群,亦可視為全體正交矩陣的乘法群。
的子群,即固定原點的全體等距同構組成的群,亦可視為全體正交矩陣的乘法群。 本身則是全體等距同構的歐氏群
本身則是全體等距同構的歐氏群 的子群。
的子群。
立體的對稱群必由等距同構組成,反之,要分析等距對稱構成的群,就是分析所有可能的對稱。有界三維立體的全體等距同構,必存在共同的不動點,不妨設其中之一為原點。
立體的對稱群,有時稱為全體對稱群作強調,用以突顯與旋轉群(或真對稱群)的分別。立體的旋轉群是其全體對稱群與三維空間本身的旋轉群 之交。立體的旋轉群等於全體對稱群,當且僅當立體具手性。
之交。立體的旋轉群等於全體對稱群,當且僅當立體具手性。
三維點群在化學廣泛用於描述分子的對稱,及組成共價鍵的分子軌域的對稱。此背景下,也稱分子對稱群。
有限考克斯特群是一族特殊的點群,僅由過原點的若干個鏡射生成。 階考克斯特群是由
階考克斯特群是由 個鏡射生成,可以考克斯特-丹金圖表示。考克斯特符號則改為用方括號和數字描述,並設有其他標記,用以表示旋轉群或其他子群。
個鏡射生成,可以考克斯特-丹金圖表示。考克斯特符號則改為用方括號和數字描述,並設有其他標記,用以表示旋轉群或其他子群。
 是直接歐氏群
是直接歐氏群 的子群,其元素皆是直接等距同構,即保持定向的等距變換。
的子群,其元素皆是直接等距同構,即保持定向的等距變換。 僅含保持原點不變的直接等距同構。
僅含保持原點不變的直接等距同構。
 則是
則是 與點反演生成的群
與點反演生成的群 的直積:(此處點反演以其矩陣
的直積:(此處點反演以其矩陣 表示,即單位矩陣
表示,即單位矩陣 乘上
乘上 。)
。)

所以,三維空間中,藉點反演,可以得到直接與間接等距變換之間的一一對應,此外, 中僅由直接等距變換組成的子群
中僅由直接等距變換組成的子群 (必包含在
(必包含在 中,亦與
中,亦與 中含有點反演的子群
中含有點反演的子群 一一對應。對應關係如下:
一一對應。對應關係如下:


例如,若 為
為 ,則
,則 為
為 ;若
;若 為
為 ,則
,則 為
為 。(定義載於下文。)
。(定義載於下文。)
若直接等距同構群 有指數為
有指數為 的子群
的子群 ,則除以上含點反演的子群外,還有另一個對應的子群
,則除以上含點反演的子群外,還有另一個對應的子群

含有間接等距變換,但不含點反演。式中 與
與 視為等同。舉例
視為等同。舉例 為
為 ,而
,而 為
為 。
。
換言之, 是將
是將 中的變換,乘上
中的變換,乘上 得到。此群
得到。此群 作為抽象群與
作為抽象群與 同構。反之,任意對稱群,若有間接等距變換,但無點反演,則可以將所有間接變換反演,而變成旋轉群。等距群的分類(見下文)中,可以用此性質化簡問題。
同構。反之,任意對稱群,若有間接等距變換,但無點反演,則可以將所有間接變換反演,而變成旋轉群。等距群的分類(見下文)中,可以用此性質化簡問題。
二維情況下, 重旋轉的循環群
重旋轉的循環群 皆是
皆是 和
和 的正規子群。在三維中,固定旋轉軸,則相應有繞該軸的
的正規子群。在三維中,固定旋轉軸,則相應有繞該軸的 重循環群
重循環群 ,是繞該軸的全體旋轉群的正規子群。此外,由於指數為
,是繞該軸的全體旋轉群的正規子群。此外,由於指數為 的子群必正規,
的子群必正規, 在
在 中正規,也在
中正規,也在 中正規。此處
中正規。此處 是向
是向 添加過旋轉軸的反射面生成,而
添加過旋轉軸的反射面生成,而 則是向
則是向 添加與軸垂直的反射面生成。
添加與軸垂直的反射面生成。
 的等距變換中,固定原點的變換,組成正交群
的等距變換中,固定原點的變換,組成正交群 ,簡記為
,簡記為 。其元素分類如下:
。其元素分類如下:
- 子群
 中:
中: - 單位(恆等變換);
- 繞過原點某軸的旋轉,且角度不為
 ;
; - 繞過原點某軸的旋轉,且角度為
 ;
;
- 及以上變換但額外乘上點反演(將向量
 映去
映去 ),即:
),即: - 點反演;
- 繞過原點的某軸,作角度不為
 的旋轉,後再作一次鏡射,鏡射面過原點,且與旋轉軸垂直;
的旋轉,後再作一次鏡射,鏡射面過原點,且與旋轉軸垂直; - 關於過原點某平面的鏡射。
後三種元素又稱瑕旋轉。(視乎定義,末一種未必算。)
連同平移變換的簡介,見歐幾里得群。
比較兩件立體的對稱類時,原點可以分別選取,即兩件立體的中心不必相同。更甚者,兩件立體具有相同對稱類,意思是其對稱群 在
在 中為共軛子群,即存在
中為共軛子群,即存在 ,使
,使 。
。
舉例:
- 兩件立體各僅有鏡射對稱,即使並非關於同一鏡面,仍屬同樣的對稱類;
- 同樣,若各僅有三重旋轉對稱,即使軸向不同,仍屬同樣的對稱類。
若立體的對稱群有多條旋轉軸或多個鏡面,或兩者皆有,則兩個對稱群同屬一類,當且僅當有另一個旋轉 ,將前一個對稱群的整個結構,變換成後一個對稱群。(此種旋轉會多於一個,但不會是無窮多個。僅有一條旋轉軸或一個鏡面時,此種旋轉方會有無窮多個。)按定義,上文的
,將前一個對稱群的整個結構,變換成後一個對稱群。(此種旋轉會多於一個,但不會是無窮多個。僅有一條旋轉軸或一個鏡面時,此種旋轉方會有無窮多個。)按定義,上文的 不必為旋轉,也可以為鏡射,然而,由於對稱群的結構不具手性,祇需取
不必為旋轉,也可以為鏡射,然而,由於對稱群的結構不具手性,祇需取 為旋轉。(但空間群則不然,有
為旋轉。(但空間群則不然,有 對空間群具有手性,因為有螺旋變換。)
對空間群具有手性,因為有螺旋變換。)
有許多無窮等距變換群,如繞任意軸轉任意無理角度(即圈數或度數為無理數,或弧度數為 的無理數倍)的旋轉,所生成的無窮循環群;若加入繞同一軸的其他旋轉,還可以組成許多非循環的交換群。取不共軸的旋轉,則生成非交換群。一般而言,此等非交換群皆為自由群。僅有特別選取的旋轉,方能得到有限群,否則一般皆是無窮群。
的無理數倍)的旋轉,所生成的無窮循環群;若加入繞同一軸的其他旋轉,還可以組成許多非循環的交換群。取不共軸的旋轉,則生成非交換群。一般而言,此等非交換群皆為自由群。僅有特別選取的旋轉,方能得到有限群,否則一般皆是無窮群。
作為拓撲群 的子群,上述無窮子群皆非閉子群。以下討論
的子群,上述無窮子群皆非閉子群。以下討論 的拓撲閉子群:
的拓撲閉子群:
 無標記特定點的球面,對稱群為
無標記特定點的球面,對稱群為 。
。 - 整個
 是球對稱群、
是球對稱群、 - 相應的旋轉群是
 、
、 - 其他無窮等距變換群有五個,皆含有過原點的某軸,繞該軸的所有旋轉,另外可以:
- 添加或不添加過軸的各鏡面反射,
- 另添加或不添加過原點與軸垂直的鏡面反射。(共四個)
- 最後,若以上兩種反射都無添加,則可以只添加兩者的複合,相當於添加與原旋轉軸垂直的軸上的
 旋轉。(一個)
旋轉。(一個)
添加過軸的各鏡面反射的群,不論有否添加過原點與軸垂射的鏡面反射,稱為兩種圓柱對稱性。注意若物理實體有無窮旋轉對稱,則亦必關於過軸的鏡面對稱。
此七個連續群,稱為極限點群或居里極限群,得名自最早研究此種群的皮埃尔·居里。[1][2]軸向群可以分成七列無窮序列,其極限給出五個軸向極限群(有兩個重複),而 、
、 則不是軸向群的極限。國際記號中,此七個群記為
則不是軸向群的極限。國際記號中,此七個群記為 ,次序在下文明確給出。[3]
,次序在下文明確給出。[3]
三維空間的對稱中,保持原點不動,等價於保持以原點為球心的球面。關於有限的三維點群,亦可參見球面有限對稱群列表。
不別共軛之異,三維有限點群只有:
 個無窮列,此七類群中,每個群至多一條旋轉軸有多於兩重旋轉。該些群皆是圓柱面的對稱群(的有限子群),其中圓柱面有限長或無限長是等價的,有時稱為軸向點群(英語:axial point groups)或棱柱點群(英語:prismatic point groups)。
個無窮列,此七類群中,每個群至多一條旋轉軸有多於兩重旋轉。該些群皆是圓柱面的對稱群(的有限子群),其中圓柱面有限長或無限長是等價的,有時稱為軸向點群(英語:axial point groups)或棱柱點群(英語:prismatic point groups)。 個其他點群,每個有至少兩條至少三重的旋轉軸;也可以等價寫成有至少兩條三重旋轉軸,因為全部七個都有多條三重旋轉軸。若數出其三重以上的旋轉軸,所有可能組合有:
個其他點群,每個有至少兩條至少三重的旋轉軸;也可以等價寫成有至少兩條三重旋轉軸,因為全部七個都有多條三重旋轉軸。若數出其三重以上的旋轉軸,所有可能組合有:  條三重軸、
條三重軸、 條三重軸及
條三重軸及 條四重軸、
條四重軸、 條三重軸及
條三重軸及 條五重軸。
條五重軸。
根據晶體學限制定理,僅得很少點群與離散平移對稱相容:七列軸向點群中,有 個;七個其他點群中,有
個;七個其他點群中,有 個,合共
個,合共 個,稱為晶體學點群。
個,稱為晶體學點群。
有七列軸向點群。每列有無窮多個群,各可用正整數 標示。每列第
標示。每列第 個群,含繞某軸的
個群,含繞某軸的 重旋轉,即旋轉
重旋轉,即旋轉 ,故
,故 對應轉一整圈,即不旋轉。七列軸向點群中,四列無其他旋轉軸(稱循環對稱),另三列有其他二重旋轉軸(稱二面對稱)。該些群可以視為二維點群添加軸向坐標和關於軸的反射而成,也與帶群相關。[4] 可以將軸向點群理解為帶群的圖案在繞柱面恰好重複
對應轉一整圈,即不旋轉。七列軸向點群中,四列無其他旋轉軸(稱循環對稱),另三列有其他二重旋轉軸(稱二面對稱)。該些群可以視為二維點群添加軸向坐標和關於軸的反射而成,也與帶群相關。[4] 可以將軸向點群理解為帶群的圖案在繞柱面恰好重複 次。
次。
下表列出點群的幾種記號:晶體學的赫爾曼–莫甘記號、分子對稱性的熊夫利記號、軌形記號、考克斯特記號。後三者不僅方便讀出群的性質,還與群的階數密切相關。軌形記號同時通用於牆紙群與帶群。晶體群的 僅能取
僅能取 (晶體學限制定理),而若移除該限制,則
(晶體學限制定理),而若移除該限制,則 可取任意正整數。七列軸向點群為:
可取任意正整數。七列軸向點群為:
| 赫-莫 | 熊夫利 | 軌形 | 考克斯特 | 帶群 | 抽象結構
(群階) | 例子 | 備註 |
 偶 偶 |  奇 奇 | (圓柱) |
 |  |  | ![{\displaystyle [n]^{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8fd1512b58cb7224224423f3aecaa36f6fcfe41)
   | p1 | 循環群
( ) ) |  |  重旋轉對稱 重旋轉對稱 |
 |  |  |  | ![{\displaystyle [2n^{+},2^{+}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e857b2c0445f52f4f65d59fd5a20524a3683f0e)
      | p11g | 
( ) ) |  |  重旋轉反射對稱 重旋轉反射對稱
勿與 次抽象對稱群混淆 次抽象對稱群混淆 |
 |  |  |  | ![{\displaystyle [n^{+},2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21a951fabff143f4153fe510eda5a38edcf60f63)
     | p11m | 
( ) ) |  | |
 |  |  |  | ![{\displaystyle [n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a26847bfc29bbeb4d6ef62ac3fd076378c0fd1db)
   | p1m1 | 二面體群
( ) ) |  | 稜錐對稱
生物學又稱雙輻射狀對稱 |
 |  |  |  | ![{\displaystyle [n,2]^{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59bb56e56445918a699ec8c41eb05090972b2498)
     | p211 | 
( ) ) |  | 二面體對稱 |
 |  |  |  | ![{\displaystyle [2n,2^{+}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e5c611a958bc30281d75790ebd79d660a149ded)
      | p2mg | 
( ) ) |  | 反稜柱對稱 |
 |  |  |  | ![{\displaystyle [n,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2a5a13f880965b785908e72d8430a2f17dc34d1)
     | p2mm | 
( ) ) | 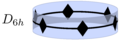 | 稜柱對稱 |
對奇數 ,有抽象群同構
,有抽象群同構 及
及 。
。
群 (包括平凡群
(包括平凡群 )及
)及 有手性,其他則無手性。
有手性,其他則無手性。
術語水平(horizontal, h)與豎直(vertical, v)描述反射面的方向,以旋轉軸為豎直,故反射面水平即垂直於與旋轉軸,反射面豎直即包含為旋轉軸。相應下標用字母h和v。
最簡單的非平凡軸向群皆同構於抽象群 ,但是
,但是 的不同子群(即不共軛):
的不同子群(即不共軛):
 (等同
(等同 )——點反演對稱
)——點反演對稱 ——二重旋轉對稱
——二重旋轉對稱 (等同
(等同 和
和 )——反射對稱,生物學又稱兩側對稱(英語:bilateral symmetry)。
)——反射對稱,生物學又稱兩側對稱(英語:bilateral symmetry)。
 七條圓柱形帶上,印有不同圖樣,使各自的對稱群等於七列軸向群中,取
七條圓柱形帶上,印有不同圖樣,使各自的對稱群等於七列軸向群中,取 的情況。
的情況。 第一組單軸循環群中, 的階為
的階為 (二維情況同樣適用),是由單一個角度為
(二維情況同樣適用),是由單一個角度為 的旋轉生成。若向此群加入一個與軸垂直的鏡面(的反射),則生成
的旋轉生成。若向此群加入一個與軸垂直的鏡面(的反射),則生成 ,階為
,階為 。若不加入與軸垂直的鏡面,但加入
。若不加入與軸垂直的鏡面,但加入 塊通過軸的鏡面,則得到
塊通過軸的鏡面,則得到 ,階亦為
,階亦為 。後者是正
。後者是正 稜錐的對稱群。具
稜錐的對稱群。具 或
或 的典型物體是螺旋槳。
的典型物體是螺旋槳。
若上述兩種鏡面皆加入,則水平鏡面與豎直鏡面相交得到 條軸,而鏡射的複合生成繞該些軸的
條軸,而鏡射的複合生成繞該些軸的 旋轉,故群不再單軸。新群的階為
旋轉,故群不再單軸。新群的階為 ,記為
,記為 。其旋轉子群為
。其旋轉子群為 個元素的二面體群
個元素的二面體群 ,仍有與主(
,仍有與主( 重)旋轉軸垂直的二重旋轉軸,但不再有鏡面。
重)旋轉軸垂直的二重旋轉軸,但不再有鏡面。
注意,在二維, 包括鏡射,但鏡射也可以視為將不辨前後之別的扁平物體翻轉得到。但在三維,鏡射與翻轉不再相同:群
包括鏡射,但鏡射也可以視為將不辨前後之別的扁平物體翻轉得到。但在三維,鏡射與翻轉不再相同:群 有翻轉但無鏡射。
有翻轉但無鏡射。
餘下一類是 (或
(或 ),其有包含主旋轉軸的豎直鏡面,但沒有水平鏡面,取而代之的操作是先水平鏡射,再旋轉
),其有包含主旋轉軸的豎直鏡面,但沒有水平鏡面,取而代之的操作是先水平鏡射,再旋轉 。
。 是正
是正 棱柱和雙稜錐的對稱群。
棱柱和雙稜錐的對稱群。 則是正
則是正 角反棱柱的對稱群,亦是正
角反棱柱的對稱群,亦是正 方偏方面體的對稱群。最後,
方偏方面體的對稱群。最後, 是稍稍扭過的正
是稍稍扭過的正 棱柱的對稱群。
棱柱的對稱群。
 及
及 較特殊,因為並無特別的主旋轉軸:三條互相垂直的旋轉軸皆為二重軸。
較特殊,因為並無特別的主旋轉軸:三條互相垂直的旋轉軸皆為二重軸。 是下節所有多面體對稱群的子群,而
是下節所有多面體對稱群的子群,而 則是多面體群
則是多面體群 與
與 的子群。
的子群。 可以作為下列化學品的對稱群:
可以作為下列化學品的對稱群:
 的元素,與利普希茨四元數的可逆元表示的旋轉,有一對二的關係。
的元素,與利普希茨四元數的可逆元表示的旋轉,有一對二的關係。
群 由「先關於水平面作鏡射,再旋轉
由「先關於水平面作鏡射,再旋轉 」生成。對於奇數
」生成。對於奇數 ,是等於前述兩個操作分開執行,生成的群
,是等於前述兩個操作分開執行,生成的群 ,階為
,階為 ,故不必用到記號
,故不必用到記號 。然而,對偶數
。然而,對偶數 ,兩個群有差異,且
,兩個群有差異,且 僅有
僅有 個元素。與
個元素。與 類似,其包含若干瑕旋轉,但不包含對應的旋轉。
類似,其包含若干瑕旋轉,但不包含對應的旋轉。
七列軸向群的元素僅有下列四對重複:
 及
及 :階數為
:階數為 ,由獨一個鏡射生成。又稱
,由獨一個鏡射生成。又稱 。
。 與
與 :階數為
:階數為 ,由獨一個
,由獨一個 旋轉生成。
旋轉生成。 與
與 :階數為
:階數為 ,由一個鏡射與鏡面上一條軸的
,由一個鏡射與鏡面上一條軸的 旋轉生成。
旋轉生成。 與
與 :階數為
:階數為 ,由一個鏡射與一條垂直於鏡面的軸的
,由一個鏡射與一條垂直於鏡面的軸的 旋轉生成。
旋轉生成。
 是由獨一個點反演生成的
是由獨一個點反演生成的 階群,又記為
階群,又記為 。
。
此處「重複」是指作為 的子群共軛,是強於作為抽象群代數同構的條件。例如,前一種意義下,有三個不同的
的子群共軛,是強於作為抽象群代數同構的條件。例如,前一種意義下,有三個不同的 階群,但祇有一個
階群,但祇有一個 階抽象群。類似,也有
階抽象群。類似,也有 與
與 抽象同構。
抽象同構。
群的構造亦可描述如下:
 是由獨一個元素生成,生成元亦稱為
是由獨一個元素生成,生成元亦稱為 ,是繞軸轉
,是繞軸轉 。群的元素是:
。群的元素是: (單位元),
(單位元), ,對應旋轉角
,對應旋轉角 。該軸視為豎直軸。
。該軸視為豎直軸。 由獨一個元素
由獨一個元素 生成,其中
生成,其中 是水平面的鏡射。群的元素是
是水平面的鏡射。群的元素是 的元素,另加
的元素,另加 。
。 由
由 與反射
與反射 生成。群的元素是
生成。群的元素是 的元素,另加
的元素,另加 。
。 由
由 與豎直鏡面的反射
與豎直鏡面的反射 生成。群的元素是
生成。群的元素是 的元素,另加
的元素,另加 。
。 是由
是由 與繞水平面上某軸
與繞水平面上某軸 的旋轉
的旋轉 ,其元素是
,其元素是 的元素,另加
的元素,另加 。
。 由元素
由元素 與
與 生成。元素是
生成。元素是 的元素,加上
的元素,加上 與
與 的額外元素,再加上
的額外元素,再加上 。
。 由元素
由元素 生成。其元素為
生成。其元素為 的元素,再加上
的元素,再加上 的所有額外元素。
的所有額外元素。
取 趨向
趨向 的極限,則得到連續軸向群(或無窮階軸向群):
的極限,則得到連續軸向群(或無窮階軸向群):
| 赫-莫 | 熊夫利 | 軌形 | 考克斯特 | 是何序列的極限 | 抽象群 |
 |  |  | ![{\displaystyle [\infty ]^{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99e8a302a0a7cc4f131bd251af0f9c1ee3161dc1) |    |  |  |  |
 |  |  | ![{\displaystyle [2,\infty ^{+}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b540e77f9a747921ee0ece4268301bbd0085999c) |      |  |  |  |
 |  |  | ![{\displaystyle [\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfdcbe72d62c10ca3f44aa9a024a24e3cb4370d8) |    |  |  |  |
 |  |  | ![{\displaystyle [2,\infty ]^{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8fc13ec6efae194a63b90149dd4a7d523dcbf9e) |      |  |  |  |
 |  |  | ![{\displaystyle [2,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d887ffa5ee329934aae77a59e76ae9d2d8441156) |      |  |  |  |
餘下七個點群又稱為高度對稱或多面體對稱,因為有多於一條旋轉軸的重數大於二。下表中, 表示一條
表示一條 重軸,即旋轉角為
重軸,即旋轉角為 ,
, 則表示同樣旋轉角的瑕旋轉軸。所用記號,首先是字母表示的熊夫利記號,然後括號內為軌形記號,然後為考克斯特記號及圖,最後是赫爾曼–莫甘記號及倘有的簡寫。
則表示同樣旋轉角的瑕旋轉軸。所用記號,首先是字母表示的熊夫利記號,然後括號內為軌形記號,然後為考克斯特記號及圖,最後是赫爾曼–莫甘記號及倘有的簡寫。

![{\displaystyle [3,3]^{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/457ba0c5ab0db8a8bb66edefe10f482a287619e6) ( (     ) )

階為 | 手性四面體對稱 | 有四條 軸,是立方體的四條體對角線,也可以看成正四面體四個頂點分別到對面中心的連線。另有三條 軸,是立方體的四條體對角線,也可以看成正四面體四個頂點分別到對面中心的連線。另有三條 軸,是立方體三組對面的中心連線,也是正四面體三組對邊的中點連線。 軸,是立方體三組對面的中心連線,也是正四面體三組對邊的中點連線。 同構交錯群 同構交錯群 ,即四個元素的偶排列的群。本群為正四面體的旋轉群,也是 ,即四個元素的偶排列的群。本群為正四面體的旋轉群,也是 及以下兩種八面體對稱群的正規子群。本群的 及以下兩種八面體對稱群的正規子群。本群的 個元素,與赫維茲四元數的 個元素,與赫維茲四元數的 個可逆元,有一對二的關係,而後者又稱為二元四面體群。 個可逆元,有一對二的關係,而後者又稱為二元四面體群。 |

![{\displaystyle [3,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4fc3992e9e923c46d4e8d5b9442864dac7b9349) ( (     ) )

階為 | 全四面體對稱 | 本群與 有相同的旋轉軸,但另有六塊鏡面,每塊經過立方體的兩條不在同一面的平行邊,也是正四面體六條稜各自的垂直平分面。每塊鏡面包含一條 有相同的旋轉軸,但另有六塊鏡面,每塊經過立方體的兩條不在同一面的平行邊,也是正四面體六條稜各自的垂直平分面。每塊鏡面包含一條 軸,兩條 軸,兩條 軸。原 軸。原 軸,加入鏡射後,變成 軸,加入鏡射後,變成 軸。本群是正四面體的對稱群。 軸。本群是正四面體的對稱群。 同構於 同構於 個元素的對稱群 個元素的對稱群 ,因為 ,因為 的元素,會將 的元素,會將 條 條 軸重新排列,而元素與此四條軸的排列一一對應。若一件物體繞其中一條三重軸,有 軸重新排列,而元素與此四條軸的排列一一對應。若一件物體繞其中一條三重軸,有 對稱,則在 對稱,則在 作用下,軌道有四件同樣的物體, 作用下,軌道有四件同樣的物體, 就對應此四件物體的排列的集合。 就對應此四件物體的排列的集合。 是 是 的正規子群。 的正規子群。 |

![{\displaystyle [3^{+},4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06076f045bf329f80409dcfca4e70becca41cd5d) ( (     ) )

階為 | 五角十二面體對稱 |  排球的縫線有 排球的縫線有 。(立方五角十二面體)本群與 。(立方五角十二面體)本群與 的旋轉軸相同,另有與立方體的面平行的鏡面。四條 的旋轉軸相同,另有與立方體的面平行的鏡面。四條 軸變成 軸變成 軸,並有關於中心的反演對稱。 軸,並有關於中心的反演對稱。 同構於 同構於 (因為 (因為 與 與 皆是正規子群),而與對稱群 皆是正規子群),而與對稱群 不同構。若在立方體的每個面上,各畫一條線段,將該面分成兩個全等的長方形,且使得新增的線段不會相交於稜上,則所得的圖形的對稱群為 不同構。若在立方體的每個面上,各畫一條線段,將該面分成兩個全等的長方形,且使得新增的線段不會相交於稜上,則所得的圖形的對稱群為 。該些對稱是:立面體四條體對角線的偶排列,及該等偶排列與中心反演的複合。本群亦是五角十二面體的對稱群。五角十二面體與前述的(面經分割的)立方體類似,但其中每個長方形換成有四邊等長,具一條對稱軸的五角形,而五角形餘下一條不同長度的邊,對應立方體的面上新增的線段。換言之,可以想像立方體的面在分割線隆起,並在該處變窄(即分割線變短)。本群為全二十面體對稱群的子群(但不正規),且是作為等距變換群的子群,而不僅是抽象子群。全二十面體對稱群有十條三重軸,而本群有其中四條。本群亦為 。該些對稱是:立面體四條體對角線的偶排列,及該等偶排列與中心反演的複合。本群亦是五角十二面體的對稱群。五角十二面體與前述的(面經分割的)立方體類似,但其中每個長方形換成有四邊等長,具一條對稱軸的五角形,而五角形餘下一條不同長度的邊,對應立方體的面上新增的線段。換言之,可以想像立方體的面在分割線隆起,並在該處變窄(即分割線變短)。本群為全二十面體對稱群的子群(但不正規),且是作為等距變換群的子群,而不僅是抽象子群。全二十面體對稱群有十條三重軸,而本群有其中四條。本群亦為 的正規子群。雖然記作 的正規子群。雖然記作 ,本群並非任何四面體(英語:Tetrahedron)的對稱群。 ,本群並非任何四面體(英語:Tetrahedron)的對稱群。 |

![{\displaystyle [4,3]^{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8d8fc11dd3e62991a585463954d84cc4d75bcae) ( (     ) )

階為 | 手性八面體對稱 | 本群與 類似,但各 類似,但各 軸現改成 軸現改成 軸,並有額外六條 軸,並有額外六條 軸,是過正方體中心與(六對)稜中點的直線。本群與 軸,是過正方體中心與(六對)稜中點的直線。本群與 同構,因為其元素與四條三重軸的 同構,因為其元素與四條三重軸的 個排列一一對應,與 個排列一一對應,與 類似。若物體繞某條三重軸有 類似。若物體繞某條三重軸有 對稱,則在 對稱,則在 作用下,軌道有四件同樣的物體,而 作用下,軌道有四件同樣的物體,而 的元素也一一對應此四件物體的排列。本群是立方體與正八面體的旋轉群。若用四元數表示旋轉,則 的元素也一一對應此四件物體的排列。本群是立方體與正八面體的旋轉群。若用四元數表示旋轉,則 對應 對應 個赫維茲四元數的可逆元及範數平方為 個赫維茲四元數的可逆元及範數平方為 的 的 個利普希茨四元數,各除以 個利普希茨四元數,各除以 。與 。與 類似,此為一對二的關係。 類似,此為一對二的關係。 |

![{\displaystyle [4,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd04791b3892c11ccd43fdc362dbc453a4f8c661) ( (     ) )

階為 | 全八面體對稱 | 本群與 有同樣的旋轉軸,但也有鏡射,有齊 有同樣的旋轉軸,但也有鏡射,有齊 與 與 的所有鏡面。本群同構於 的所有鏡面。本群同構於 (因為 (因為 與 與 皆為正規子群),且是立方體與正八面體的對稱群。見八面體對稱。 皆為正規子群),且是立方體與正八面體的對稱群。見八面體對稱。 |

![{\displaystyle [5,3]^{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33a41176db28aee72ba144dacc90b14ecd19e6e1) ( (     ) )

階為 | 手性二十面體對稱 | 本群為正二十面體與正十二面體的旋轉群,亦是全正二十面體對稱群 的指標 的指標 正規子群。本群的子群中,有十個 正規子群。本群的子群中,有十個 與六個 與六個 (即稜柱或反稜柱的旋轉群)。本群也包含五個 (即稜柱或反稜柱的旋轉群)。本群也包含五個 子群(見五複合正四面體)。抽象而言, 子群(見五複合正四面體)。抽象而言, 同構於 同構於 次交錯群 次交錯群 ,因為其元素作用在五個 ,因為其元素作用在五個 子群上,與其偶排列一一對應。等價地,可以考慮 子群上,與其偶排列一一對應。等價地,可以考慮 對前述五複合正四面體的五個單體的作用。以四元數表示旋轉,則 對前述五複合正四面體的五個單體的作用。以四元數表示旋轉,則 對應 對應 個二十數可逆元。與先前一樣,此為一對二的關係。 個二十數可逆元。與先前一樣,此為一對二的關係。 |

![{\displaystyle [5,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b40aefcb9064b92a37fd6e8c1b5a1777cfea0b92) ( (     ) )

階為 | 全二十面體對稱 | 本群為正二十面體與正十二面體的對稱群。 與抽象群 與抽象群 同構,因為 同構,因為 與 與 皆是正規子群。本群的子群中,有十個 皆是正規子群。本群的子群中,有十個 、六個 、六個 (反稜柱的對稱)、五個 (反稜柱的對稱)、五個 。 。 |
相關的連續群有:
- 旋轉群
 ,即所有旋轉的群,亦記作
,即所有旋轉的群,亦記作 或
或 。
。 - 正交群
 ,所有旋轉和鏡射生成的群,亦記作
,所有旋轉和鏡射生成的群,亦記作 或
或 。
。
如無窮等距變換群一節所言,任何物理實體,若有 對稱性,則必有
對稱性,則必有 對稱性。
對稱性。
若已知群的軌形記號,則可計算其階數,等於 除以軌形的歐拉示性數。軌形的歐拉示性數是將
除以軌形的歐拉示性數。軌形的歐拉示性數是將 減去軌形記號中,各符號特徵數的總和:
減去軌形記號中,各符號特徵數的總和:
- 無
 或在
或在 之前的
之前的 ,值為
,值為 ;
; - 在
 之後的
之後的 ,值為
,值為 ;
;  與
與 計為
計為 。
。
此公式同樣適用於壁紙群與帶群:對該等群,特徵數之和為 ,所以階數是無窮大。亦見壁紙群條目。
,所以階數是無窮大。亦見壁紙群條目。
三維考克斯特群的基本域 ![{\displaystyle A_{3},\ [3,3],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bd7a86e3594f0225a587950c771f6fb637b736d)      | ![{\displaystyle B_{3},\ [4,3],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2413b2f708b30512f825cf5e4f057fcd86a9b435)      | ![{\displaystyle H_{3},\ [5,3],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4da5c46e9fd13305e577622f97b2f0caa7b12b16)      |

 塊鏡 塊鏡 | 
 塊鏡 塊鏡 | 
 塊鏡 塊鏡 |
![{\displaystyle 2A_{1},\ [1,2],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/077092ca401f4283e403d3c6185bd3cb2a6fc39f)    | ![{\displaystyle 3A_{1},\ [2,2],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aab459801df5a6d9bb8794a27b3f274bc8e5b2bb)      | ![{\displaystyle A_{1}A_{2},\ [2,3],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d7f1c1fb7ccf3ce1c90ba3c78afb931b400d259)      |

 塊鏡 塊鏡
|


































































![{\displaystyle [n]^{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8fd1512b58cb7224224423f3aecaa36f6fcfe41)





![{\displaystyle [2n^{+},2^{+}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e857b2c0445f52f4f65d59fd5a20524a3683f0e)




![{\displaystyle [n^{+},2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21a951fabff143f4153fe510eda5a38edcf60f63)




![{\displaystyle [n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a26847bfc29bbeb4d6ef62ac3fd076378c0fd1db)





![{\displaystyle [n,2]^{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59bb56e56445918a699ec8c41eb05090972b2498)




![{\displaystyle [2n,2^{+}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e5c611a958bc30281d75790ebd79d660a149ded)





![{\displaystyle [n,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2a5a13f880965b785908e72d8430a2f17dc34d1)









































![{\displaystyle [\infty ]^{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99e8a302a0a7cc4f131bd251af0f9c1ee3161dc1)




![{\displaystyle [2,\infty ^{+}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b540e77f9a747921ee0ece4268301bbd0085999c)






![{\displaystyle [\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfdcbe72d62c10ca3f44aa9a024a24e3cb4370d8)




![{\displaystyle [2,\infty ]^{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8fc13ec6efae194a63b90149dd4a7d523dcbf9e)



![{\displaystyle [2,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d887ffa5ee329934aae77a59e76ae9d2d8441156)




![{\displaystyle [3,3]^{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/457ba0c5ab0db8a8bb66edefe10f482a287619e6)







![{\displaystyle [3,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4fc3992e9e923c46d4e8d5b9442864dac7b9349)




![{\displaystyle [3^{+},4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06076f045bf329f80409dcfca4e70becca41cd5d)



![{\displaystyle [4,3]^{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8d8fc11dd3e62991a585463954d84cc4d75bcae)





![{\displaystyle [4,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd04791b3892c11ccd43fdc362dbc453a4f8c661)




![{\displaystyle [5,3]^{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33a41176db28aee72ba144dacc90b14ecd19e6e1)







![{\displaystyle [5,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b40aefcb9064b92a37fd6e8c1b5a1777cfea0b92)











![{\displaystyle A_{3},\ [3,3],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bd7a86e3594f0225a587950c771f6fb637b736d)
![{\displaystyle B_{3},\ [4,3],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2413b2f708b30512f825cf5e4f057fcd86a9b435)
![{\displaystyle H_{3},\ [5,3],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4da5c46e9fd13305e577622f97b2f0caa7b12b16)


![{\displaystyle 2A_{1},\ [1,2],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/077092ca401f4283e403d3c6185bd3cb2a6fc39f)
![{\displaystyle 3A_{1},\ [2,2],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aab459801df5a6d9bb8794a27b3f274bc8e5b2bb)
![{\displaystyle A_{1}A_{2},\ [2,3],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d7f1c1fb7ccf3ce1c90ba3c78afb931b400d259)