Toán học của thuyết tương đối rộng

Thuyết tương đối rộng
${\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }={8\pi G \over c^{4}}T_{\mu \nu }}$
Dẫn nhập · Lịch sử · Nguyên lý toán học Kiểm chứng
Khái niệm cơ sở Thuyết tương đối hẹp Nguyên lý tương đương Tuyến thế giới · Hình học Riemann
Hiệu ứng và hệ quả Bài toán Kepler · Thấu kính · Sóng Kéo hệ quy chiếu · Hiệu ứng trắc địa Chân trời sự kiện · Điểm kì dị Lỗ đen
Phương trình Tuyến tính hóa hấp dẫn Hình thức hậu Newton Phương trình trường Einstein Phương trình đường trắc địa Phương trình Friedmann Hình thức luận ADM Hình thức luận BSSN Phương trình Hamilton–Jacobi–Einstein
Lý thuyết phát triển Kaluza–Klein Hấp dẫn lượng tử
Các nghiệm Schwarzschild Reissner–Nordström · Gödel Kerr · Kerr–Newman Kasner · Taub-NUT · Milne · Robertson–Walker Sóng-pp ·
Nhà vật lý Einstein · Lorentz · Hilbert · Poincare · Schwarzschild · Sitter · Reissner · Nordström · Weyl · Eddington · Friedman · Milne · Zwicky · Lemaître · Gödel · Wheeler · Robertson · Bardeen · Walker · Kerr · Chandrasekhar · Ehlers · Penrose · Hawking · Taylor · Hulse · Stockum · Taub · Newman · Khâu Thành Đồng · Thorne khác
Không thời gian Không gian Thời gian Đường cong thời gian đóng Lỗ sâu Không thời gian Minkowski Biểu đồ không thời gian
x t s

Toán học của thuyết tương đối rộng là mô hình chứa đựng cấu trúc và kỹ thuật toán học được sử dụng để nghiên cứu và thiết lập lên thuyết tương đối rộng của Einstein. Công cụ chính sử dụng trong lý thuyết hình học về lực hấp dẫn này là trường tenxơ xác định trên đa tạp Lorentz biểu diễn không thời gian. Bài viết này miêu tả tổng quan về toán học của thuyết tương đối tổng quát.

Ký hiệu

Trong toàn bộ bài viết, chúng ta sử dụng dấu metric kiểu không gian ${\displaystyle \scriptstyle (-,+,+,+)}$ và hệ đơn vị hình học trong đó ${\displaystyle G=c=1}$ mặc dù khi cần thiết chúng ta sẽ viết rõ tốc độ ánh sáng, c. Chúng ta sẽ viết đậm các tenxơ, ví dụ ${\displaystyle {\boldsymbol {V}}}$, và các mũi tên bên ám chỉ các vectơ ba chiều hoặc các toán tử, ví dụ ${\displaystyle {\overrightarrow {v}}}$ hoặc ${\displaystyle {\overrightarrow {\nabla }}}$. Đạo hàm hiệp biến và đạo hàm riêng bốn chiều sẽ được ký hiệu dạng tổng quát lần lượt là ${\displaystyle \nabla _{\mu }}$ và ${\displaystyle \partial _{\mu }}$ nhưng những ký hiệu khác có thể được sử dụng cho các khái niệm ít gặp hơn hoặc khi muốn so sánh với các công thức của cơ học Newton. Với quy ước chuẩn về cách tính tổng khi gặp các chỉ số lặp lại, các chỉ số Hy Lạp sẽ có giá trị từ 0 đến 3, trong khi các chỉ số Latin chạy từ 1 đến 3.

Khái niệm không thời gian[sửa | sửa mã nguồn]

Bước quan trọng đầu tiên để hiểu đúng đắn thuyết tương đối rộng, và từ đó là cấu trúc toán học của nó, chính là sự từ bỏ ý tưởng của Galilei về một không gian tuyệt đối và thời gian tuyệt đối. Hơn thế, điều này đưa đến đề xuất cách mạng về sự từ bỏ ý nghĩ không gian và thời gian như là những thành phần của một phông nền cố định, một đối tượng mà mọi quá trình xảy ra trên nó. Từ đây, các nhà vật lý cần thiết phải coi không gian và thời gian là những yếu tố động lực trong các định luật của tự nhiên, và cũng vì thế mà những định luật này bị ảnh hưỏng sâu sắc bởi chúng. Ý tưởng cách mạng này nằm ở trung tâm của thuyết tương đối và là một trong những thành tựu khoa học có ảnh hưởng lớn nhất của mọi thời đại.

Việc từ bỏ ý tưởng về một không gian tuyệt đối và một thời gian tuyệt đối dẫn tới sự giới thiệu không tránh khỏi của một khái niệm mới, đó là không thời gian, một đối tượng bốn chiều đơn nhất ${\displaystyle {\mathcal {S}}}$, mà tuy nhiên, không nên chỉ coi nó như là một sân khấu cho tiến trình của một hệ vật lý xác định, mà nó còn là một trường động lực tham gia vào sự tiến triển của chính hệ vật lý đó. Những phần tử của không thời gian trừu tượng này được gọi là sự kiện, một khái niệm dường như cũng trừu tượng nhưng không hẳn là vậy. Chúng ta chắc chắn đã quen với khái niệm "cái gì đó ở nơi nào đấy" vì nó trở thành một phần nhận thức của chúng ta về thế giới khi còn là một đứa trẻ. Tương tự, khái niệm sự kiện có thể đi kèm với ý tưởng về "cái gì đó xảy ra ở nơi nào đấy", chẳng hạn như photon từ Mặt Trời tới võng mạc của chúng ta lúc bình minh. Do đó, các nhà vật lý thích nghĩ về các sự kiện như là các "điểm" ${\displaystyle P}$ trong không thời gian ${\displaystyle {\mathcal {S}}}$, và sự tồn tại của chúng như là các phần tử của không thời gian độc lập với cách chọn hệ tọa độ để định vị chúng tại một vị trí không gian cụ thể trong một thời gian cho trước. Các sự kiện do đó tự chúng là những phần tử của không thời gian, mà tính động lực được điều chỉnh bởi các định luật vật lý.

Với tư duy như thế, các nhà vật lý nghĩ tới vấn đề các sự kiện liên hệ với nhau bằng cách nào. Nếu coi một sự kiện là "một cái gì đó xảy ra ở nơi nào đó", thì hai hay nhiều sự kiện có thể được liên hệ (vd, thông qua các định luật vật lý) và đưa vào thành "một dãy các sự kiện", mà, trong trường hợp dãy được xếp thứ tự với thời gian như là một tham số, chúng thuộc về một tập hợp, cụ thể hơn là một đường cong trong không thời gian, gọi là "đường thế giới" (worldline). Cũng trong trường hợp này, khái niệm trừu tượng về đường thế giới quả thực hiển nhiên giống với một cách giải thích quen thuộc khi chúng ta nghĩ tới tuyến đường trên một bản đồ (đoạn đường từ nhà tới nơi làm việc) như đường thế giới trong không thời gian miêu tả về chuyển động của chúng ta. Sự tài tình ở đây là, trong khi tuyến đường trên bản đồ kết nối các điểm (không gian) khác nhau mà chúng ta đứng tại những thời điểm khác nhau, thì đường thế giới kết nối các sự kiện khác nhau của không thời gian, tức là, những sự kiện mà chúng ta tham gia vào khi đi từ nhà đến nơi làm việc. Một hệ quả rõ ràng từ định nghĩa của đường thế giới là khi không có một không gian tuyệt đối và một thời gian tuyệt đối, bất kỳ sự lựa chọn theo thứ tự các sự kiện chỉ có thể là "tùy ý" (hoặc tương đối) khi có thể thay thế bằng những sự kiện tương đương và khả dĩ trên cùng một tập hợp các sự kiện. Tuy nhiên, kết quả này không nên chỉ coi đó là một giới hạn, nhưng mà là một đặc điểm quan trọng trong bức tranh mới về không gian và thời gian, một điều căn bản trong thuyết tương đối rộng. Nói chung, khái niệm như tính đồng thời vẫn được giữ lại nhưng phải được thể hiện một cách đúng đắn, và điều này được nhắc tới ở phần sau.

Đa tạp không thời gian[sửa | sửa mã nguồn]

${\displaystyle M}$

${\displaystyle U_{\alpha }}$

${\displaystyle U_{\beta }}$

${\displaystyle \varphi _{\alpha }}$

${\displaystyle \varphi _{\beta }}$

${\displaystyle \tau _{\alpha ,\beta }}$

${\displaystyle \tau _{\beta ,\alpha }}$

${\displaystyle \mathbb {R} ^{n}}$

${\displaystyle \mathbb {R} ^{n}}$

Hai bản đồ ${\displaystyle \scriptstyle \{(U_{\alpha },\varphi _{\alpha })\}\to \mathbb {R} ^{n}}$ trên đa tạp M. ${\displaystyle \scriptstyle U_{\alpha },U_{\beta }}$ là 2 tập con mở, ${\displaystyle \scriptstyle \varphi _{\alpha },\varphi _{\beta }}$ là hai ánh xạ địa phương khả vi từ các tập con mở vào không gian Euclid. Atlas của M là tập hợp các bản đồ ${\displaystyle \scriptstyle \{(U_{\alpha },\varphi _{\alpha })\}}$ sao cho ${\displaystyle \scriptstyle \bigcup U_{\alpha }=M}$. Giả sử ${\displaystyle \scriptstyle U_{\alpha }\cap U_{\beta }}$ không rỗng, khi đó ánh xạ chuyển tiếp ${\displaystyle \scriptstyle \tau _{\alpha ,\beta }:\varphi _{\alpha }(U_{\alpha }\cap U_{\beta })\to \varphi _{\beta }(U_{\alpha }\cap U_{\beta })}$ xác định bởi ${\displaystyle \scriptstyle \tau _{\alpha ,\beta }=\varphi _{\beta }\circ \varphi _{\alpha }^{-1}.}$.

Thuyết tương đối rộng đề xuất ý tưởng miêu tả các hiện tượng vật lý bằng một tập hợp các sự kiện, tạo thành một thể liên tục (continuum) bốn chiều, gọi là không thời gian. Khái niệm toán học phù hợp nhất để đặc trưng cho không thời gian đó là một đa tạp khả vi ${\displaystyle {\mathcal {M}}}$, một khái niệm kết hợp giữa những khái niệm của không gian tôpô và tính khả vi. Tức là, khi nói đến không thời gian bằng tập hợp các sự kiện, là một không gian tôpô, ta đang cung cấp thông tin về việc bằng cách nào mà những vùng khác nhau của continuum này được liên hệ với nhau. Hơn nữa, như đã rõ ràng khi ta nói về nguyên lý tương đương, thuyết tương đối rộng đòi hỏi rằng các sự kiện khác nhau của không thời gian cho phép các lân cận địa phương không giao nhau (rời nhau). Từ đây, không gian tôpô nhất thiết phải là không gian tôpô Hausdorff. Ngoài cấu trúc tôpô, ta cần trang bị cho không thời gian một cấu trúc vi phân thông qua phép tham số hóa khả vi bằng các tọa độ được gắn cho mỗi sự kiện. Những cách đặt tham số hóa này được thực hiện thông qua các hàm số của lớp ${\displaystyle C^{k}}$ với ${\displaystyle k\geq 2}$, mà ánh xạ lân cận địa phương của mỗi sự kiện vào ${\displaystyle \mathbb {R} ^{n}}$. Do vậy một đa tạp khả vi là một không gian tôpô Hausdorff vi phôi địa phương với ${\displaystyle \mathbb {R} ^{n}}$. Ví dụ đơn giản về đa tạp đó là bề mặt của một hình cầu ba chiều ("mặt cầu 2 chiều") hoặc bất kỳ một siêu mặt m chiều nào trong không gian n chiều với ${\displaystyle m\leq n}$.^[1]

Có rất nhiều sách và bài viết thảo luận về định nghĩa và tính chất của không gian tôpô và của đa tạp, chẳng hạn Franken 2011, Ch 2 và De Felice & Clarke 1992. Cho những mục đích ứng dụng chúng ta có thể coi ${\displaystyle {\mathcal {M}}}$ là "tập hợp chứa các sự kiện được tham số hóa", những thứ tạo nên không thời gian bốn chiều, và các tham số của chúng là những hàm khả vi tới một số bậc nhất định.

Số các tham số độc lập cần thiết để định ra một sự kiện trong ${\displaystyle {\mathcal {M}}}$ chính là số chiều của đa tạp và cách chọn những tham số này sẽ biểu diễn cách chọn hệ tọa độ cần thiết để phủ đa tạp, và có vô số cách chọn như thế. Ví dụ, hệ tọa độ sử dụng kinh độ và vĩ độ để xác định vị trí của điểm trên bề mặt Trái Đất. Khi áp dụng, chúng ta cần thiết định nghĩa một quy tắc gán tương ứng một điểm của đa tạp ${\displaystyle {\mathcal {M}}}$, tức là sự kiện, vào không gian thực n chiều ${\displaystyle \mathbb {R} ^{n}}$. Quy tắc này gọi là phép ánh xạ và cách chọn hệ tọa độ tương ứng sẽ phủ một phần hoặc toàn bộ đa tạp không thời gian. Các điểm lưu ý:

1. Ánh xạ thảo luận ở trên có thể coi là sự gán một - một các điểm trên đa tạp với các điểm của không gian Euclid với số chiều thích hợp. Sự tương ứng này là có ích nhưng phải cẩn thận khi áp dụng. Cụ thể hơn, nó nhấn mạnh rằng ít nhất trên cục bộ (hay địa phương) đa tạp nhìn giống như không gian Euclid.^[2] Tuy nhiên nó cũng ẩn chứa thực tế rằng tô pô toàn cục của đa tạp có thể rất khác so với tô pô Euclid. Chẳng hạn đa tạp là bề mặt của hình vòng xuyến: cả bề mặt lẫn tô pô toàn cục của nó khác hẳn so với không gian Euclid, nhưng có thể ánh xạ cục bộ một diện tích nhỏ trên bề mặt vào không gian Euclid, như mặt phẳng tiếp xúc với một điểm trong diện tích này.
2. Trong khi có vô hạn cách chọn hệ tọa độ để phủ một đa tạp, không phải cách nào cũng cho phương án tốt. Một số hệ tọa độ trong chúng có thể suy biến và khi phân tích toán học nghiệm của phương trình trường Einstein chứa đựng hệ tọa độ cho phép làm nổi bật nhất ý nghĩa vật lý của nghiệm. Lấy ví dụ lần nữa về hệ tọa độ cầu ${\displaystyle (\theta ,\phi )}$ trên mặt cầu 2 chiều. Rõ ràng hệ tọa độ này suy biến tại hai cực của mặt cầu vì có thể ánh xạ những tập vô hạn các giá trị, ví dụ khi ${\displaystyle \theta =0,\pi }$ và ${\displaystyle \phi \in [0,2\pi ]}$.
3. Mỗi hệ tọa độ bao phủ một vùng nhất định của không thời gian gọi là mảnh hay bản đồ, và hai bản đồ có thể có miền giao nhau hoặc không. Atlas của đa tạp là bất kỳ những phép hợp các bản đồ sao cho phép hợp này bao phủ toàn bộ đa tạp.
4. Như đã nêu ở trên, mộ tính chất cơ bản của đa tạp trong thuyết tương đối rộng đó là chúng có tính khả vi, nghĩa là ánh xạ địa phương từ đa tạp vào ${\displaystyle \mathbb {R} ^{n}}$ phải khả vi. Mặt cầu hai chiều là đa tạp khả vi trong khi hình nón thì không, do nó không khả vi tại đỉnh nón vì không tồn tại ánh xạ khả vi từ điểm này vào ${\displaystyle \mathbb {R} ^{n}}$.

Hệ tọa độ[sửa | sửa mã nguồn]

Ý tưởng về không thời gian (tập hợp chứa mọi sự kiện), như là một đa tạp (không gian phủ bởi các hệ tọa độ), là rất hấp dẫn từ quan điểm hình học, nhưng cũng phải là nguồn để đề cập đến từ quan điểm vật lý học, vì sự lựa chọn tùy ý hệ tọa độ có thể đưa đến việc làm mất các thông tin vật lý. Tuy vậy, đây là một lập luận không đúng và các phép đo phải là độc lập với hệ tọa độ, tức là, các phép đo sẽ cho cùng một kết quả trong mọi hệ tọa độ được lựa chọn. Tương tự, vẫn có thể dẫn ra được các phương trình độc lập với hệ tọa độ khi không thời gian được coi là một đa tạp.

Bước đầu tiên để học quá trình này đó là làm quen với các đối tượng cơ bản của một đa tạp, như đường cong, đại lượng vô hướng và vectơ, và cách chúng biến đổi như thế nào khi chuyển từ hệ tọa độ này sang hệ tọa độ khác. Kể từ đây chúng ta giả sử rằng ${\displaystyle {\mathcal {M}}}$ là đa tạp khả vi gồm bốn chiều (ba chiều không gian và một chiều thời gian), nhưng việc tổng quát hóa các tính chất của đa tạp lên đa tạp n chiều là trực tiếp.

Xét không thời gian được phủ bởi hai hệ tọa độ,^[3] ${\displaystyle \{x^{\mu }\}}$ và ${\displaystyle \{x^{\mu '}\}}$^[4] , hoặc tương đương, xét hai ánh xạ khác nhau ${\displaystyle \Phi }$ và ${\displaystyle \Phi '}$ đi từ ${\displaystyle {\mathcal {M}}}$ vào ${\displaystyle \mathbb {R} ^{4}}$. Mỗi điểm P của ${\displaystyle {\mathcal {M}}}$ do đó được biểu diễn bằng hai tọa độ khác nhau, mỗi tọa độ chứa bốn phần tử, ${\displaystyle \{x_{P}^{\mu }\}}$ và ${\displaystyle \{x_{P}^{\mu '}\}}$. Phép biến đổi tọa độ ${\displaystyle \{x^{\mu }\}\rightarrow \{x^{\mu '}\}}$ tại điểm P được biểu diễn bằng bốn hàm số đơn trị, liên tục và khả vi ${\displaystyle f^{\mu }}$ sao cho

${\displaystyle \{x_{P}^{\mu '}\}=\left.f^{\mu '}(x^{1},x^{2},x^{3},x^{4})\right|_{P}=\left.f^{\mu '}(\mathbf {x} )\right|_{P}}$

(1)

ở đây ký hiệu x có bốn tọa độ ${\displaystyle x^{\mu }}$ ám chỉ những đối tượng bôi đậm thuộc về ${\displaystyle {\mathcal {M}}}$. Bởi vì đa tạp là khả vi, do vậy phép biến đổi tọa độ không chỉ đúng tại điểm P, tức là

${\displaystyle \{x^{\mu '}\}=f^{\mu '}(\mathbf {x} )}$

(2)

Hàm f cũng phải khả nghịch, do đó hàm f⁻¹ là phép biến đổi tọa độ nghịch đảo ${\displaystyle \{x^{\mu '}\}\rightarrow \{x^{\mu }\}}$ và

${\displaystyle \{x^{\mu }\}=(f^{-1})^{\mu }(\mathbf {x'} )}$

(3)

với phép toán kết hợp ${\displaystyle f\circ f^{-1}}$ trở thành đồng nhất, nghĩa là ${\displaystyle x^{\mu }=x^{\mu }(x^{\mu '})=x^{\mu }(x^{\mu '}(x^{\mu }))}$.

Ví dụ coi mặt phẳng là một đa tạp hai chiều với hai hệ tọa độ ${\displaystyle \{x^{\mu }\}=(x,y)}$ và ${\displaystyle \{x^{\mu '}\}=(r,\theta )}$ do vậy

${\displaystyle f:{\begin{cases}x=rcos\theta \\y=rsin\theta ,\end{cases}}\quad f^{-1}:{\begin{cases}r=(x^{2}+y^{2})^{\frac {1}{2}}\\\theta =tan^{-1}\left({\frac {y}{x}}\right),\end{cases}}}$

(4)

và nếu áp dụng hàm hợp ${\displaystyle f\circ f^{-1}}$ đối với tập tọa độ thứ nhất ta thu được đồng nhất thức ${\displaystyle x=(x^{2}+y^{2})^{\frac {1}{2}}cos[tan^{-1}(y/x)]=x.}$

Khai thác tính khả vi của đa tạp, chúng ta có thể lấy vi phân của tọa độ x' theo x và thu được ma trận biến đổi

${\displaystyle \mathbf {\Lambda } ^{\mu '}{}_{\mu }:={\frac {\partial x^{\mu '}}{\partial x^{\mu }}}=\left({\begin{array}{rrrr}{\dfrac {\partial x^{0'}}{\partial x^{0}}}&{\dfrac {\partial x^{0'}}{\partial x^{1}}}&{\dfrac {\partial x^{0'}}{\partial x^{2}}}&{\dfrac {\partial x^{0'}}{\partial x^{3}}}\\{\dfrac {\partial x^{1'}}{\partial x^{0}}}&{\dfrac {\partial x^{1'}}{\partial x^{1}}}&{\dfrac {\partial x^{1'}}{\partial x^{2}}}&{\dfrac {\partial x^{1'}}{\partial x^{3}}}\\{\dfrac {\partial x^{2'}}{\partial x^{0}}}&{\dfrac {\partial x^{2'}}{\partial x^{1}}}&{\dfrac {\partial x^{2'}}{\partial x^{2}}}&{\dfrac {\partial x^{2'}}{\partial x^{3}}}\\{\dfrac {\partial x^{3'}}{\partial x^{0}}}&{\dfrac {\partial x^{3'}}{\partial x^{1}}}&{\dfrac {\partial x^{3'}}{\partial x^{2}}}&{\dfrac {\partial x^{3'}}{\partial x^{3}}}\end{array}}\right).}$

(5)

với định thức

${\displaystyle J':=\left|{\frac {\partial x^{\mu '}}{\partial x^{\mu }}}\right|}$

(6)

là định thức Jacobi (hay Jacobian) của biến đổi tọa độ ${\displaystyle f}$ trong (2). Nếu J' khác 0 tại mọi điểm, khi đó phương trình (2) sẽ có nghiệm và chúng ta nhận được phép biến đổi ngược (3). Ngược lại, nếu J' = 0 tại một điểm, ta nói phép biến đổi là kỳ dị tại điểm đó. Tương tự ta có thể lấy vi phân tọa độ x theo x' và thu được ma trận biến đổi ngược

${\displaystyle \mathbf {\Lambda } ^{\mu }{}_{\mu '}:=\left({\frac {\partial x^{\mu }}{\partial x^{\mu '}}}\right)}$

(7)

Đến đây, sử dụng quy tắc dây chuyền đối với đạo hàm riêng, sẽ không khó để chứng minh được rằng hai ma trận (5) và (7) là nghịch đảo của nhau, tức là

${\displaystyle \mathbf {\Lambda '\Lambda } =\mathbb {I} }$

(8)

với ${\displaystyle \mathbf {\Lambda ',\Lambda } ,\mathbb {I} }$ lần lượt là các ma trận tương ứng của ${\displaystyle \Lambda ^{\mu '}{}_{\mu },\Lambda ^{\mu }{}_{\mu '}}$ và ma trận đơn vị. Hệ quả trực tiếp của (8) đó là định thức Jacobi của hai ma trận là nghịch đảo của nhau, tức là J' = 1/J.

Ví dụ ma trận biến đổi giữa hai hệ tọa độ trong (4) là

${\displaystyle \mathbf {\Lambda } '=\Lambda ^{\mu '}{}_{\mu }=\left({\begin{array}{rr}{\dfrac {\partial r}{\partial x}}&{\dfrac {\partial r}{\partial y}}\\{\dfrac {\partial \theta }{\partial x}}&{\dfrac {\partial \theta }{\partial y}}\end{array}}\right)}$

(9)

và

${\displaystyle \mathbf {\Lambda } =\Lambda ^{\mu }{}_{\mu '}=\left({\begin{array}{rr}{\dfrac {\partial x}{\partial r}}&{\dfrac {\partial x}{\partial \theta }}\\{\dfrac {\partial y}{\partial r}}&{\dfrac {\partial y}{\partial \theta }}\end{array}}\right)}$

(10)

với ${\displaystyle J'=1/(x^{2}+y^{2})^{1/2}=1/J.}$

Đường cong (curve) và quỹ đạo (path)[sửa | sửa mã nguồn]

Sau khi đã giới thiệu khái niệm hệ tọa độ và biến đổi tọa độ, bây giờ chúng ta xét tới đối tượng đơn giản nhất trong đa tạp ${\displaystyle {\mathcal {M}}}$ mà sẽ dẫn tới định nghĩa tenxơ.

Xét trong không thời gian ${\displaystyle {\mathcal {S}}}$ một chuỗi các sự kiện ${\displaystyle P_{1},...,P_{n}}$ mà được liên hệ với nhau theo những cách nào đó. Như đã nói ở mục Khái niệm không thời gian, ta có thể liên hệ hoặc xếp thứ tự các sự kiện và sẽ thu được đường thế giới (worldline) khi tham số xếp thứ tự là tọa độ thời gian t. Bây giờ chúng ta mở rộng ý tưởng và xét các sự kiện mà không nhất thiết phải liên hệ thông qua thời gian, mà thông qua một tham số tổng quát hơn là ${\displaystyle \lambda }$. Đối tượng thu được gọi là đường cong (curve) ${\displaystyle {\mathcal {C}}}$ và là ánh xạ từ một đoạn ${\displaystyle I=[a,b]}$ vào một tập hợp các điểm có tọa độ ${\displaystyle \{x^{\mu }\}}$ tức là

đường cong ${\displaystyle {\mathcal {C}}\!:\{x^{\mu }(\lambda ),\lambda \in I\}}$

(11)

Rõ ràng rằng, cùng một tập hợp các điểm trong ${\displaystyle {\mathcal {S}}}$ có thể được tham số hóa vô hạn lần khi thay đổi cách lựa chọn tham số ${\displaystyle \lambda }$. Cách xem xét này giúp chúng ta phân biệt với khái niệm quỹ đạo (path) - như là tập hợp các sự kiện trong ${\displaystyle {\mathcal {S}}}$, so với đường cong đi qua các sự kiện này. Trong khi quỹ đạo là một đối tượng nội tại trong không thời gian ${\displaystyle {\mathcal {S}}}$ thì đường cong lại phụ thuộc vào cả cách tham số hóa nó cũng như việc chọn hệ tọa độ để lập bản đồ (chart) cho đa tạp ${\displaystyle {\mathcal {M}}}$. Khi thay đổi tham số ${\displaystyle \lambda }$ sẽ dẫn tới đường cong mới đi qua cùng quỹ đạo trong ${\displaystyle {\mathcal {S}}}$ và cùng hệ tọa độ biểu diễn trong ${\displaystyle {\mathcal {M}}}$ (trong trường hợp này nó được gọi là ảnh). Tuy nhiên, khi thay đổi hệ tọa độ sẽ đem lại một đường cong mới đi qua cùng một quỹ đạo trong ${\displaystyle {\mathcal {S}}}$, nhưng rõ ràng nó sẽ không chứa cùng những tọa độ biểu diễn trong ${\displaystyle {\mathcal {M}}}$. Nói cách khác, khái niệm quỹ đạo mang ý nghĩa cơ bản hơn so với khái niệm đường cong và ảnh, chúng ta có thể xây dựng hai đường cong:

đường cong ${\displaystyle {\mathcal {C}}'\!:\{x^{\mu }(\lambda '),\lambda '\in I'\}}$

(12)

và

đường cong ${\displaystyle {\mathcal {L}}'\!:\{x^{\mu '}(\lambda '),\lambda '\in I'\}}$

(13)

sao cho chúng chứa cùng một quỹ đạo trong ${\displaystyle {\mathcal {S}}}$, với ${\displaystyle {\mathcal {C}}\!}$ và ${\displaystyle {\mathcal {C}}'}$ có cùng ảnh, nhưng ${\displaystyle {\mathcal {C}}}$ và ${\displaystyle {\mathcal {L}}'}$ có ảnh khác nhau.

Cuối cùng, chúng ta có thể mở rộng khái niệm đường cong cho một mặt với hai tham số,

mặt ${\displaystyle {\mathcal {H}}\!:\{x^{\mu }(\lambda ^{1},\lambda ^{2});\lambda ^{1},\lambda ^{2}\in I\}}$

(14)

Mặt được gọi là siêu mặt của đa tạp nếu số tham số cần thiết để miêu tả nó bằng số chiều của đa tạp trừ đi một, ví dụ siêu mặt 3 chiều đối với không thời gian bốn chiều.

Vectơ tiếp xúc[sửa | sửa mã nguồn]

xem thêm: Véctơ-4

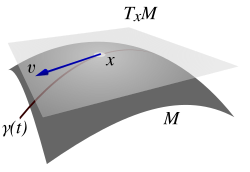
Tất cả những khái niệm đã giới thiệu về các đường cong và mặt có thể được coi như là những công cụ cơ bản để định nghĩa khái niệm rất quan trọng và hữu ích, đó là vectơ tiếp xúc (tangent vector) với đường cong ${\displaystyle {\mathcal {C}}}$. Nếu coi đường cong là tập hợp các điểm với mỗi điểm được đánh dấu bởi một bộ các tọa độ sắp thứ tự bằng một tham số λ, thì vectơ tiếp xúc là khái niệm dùng để diễn giải sự thay đổi tọa độ như thế nào dọc theo đường cong này. Nói cách khác, khi cho trước một hệ tọa độ ${\displaystyle \{x^{\mu }\}}$ trong đa tạp ${\displaystyle {\mathcal {M}}}$ và một đường cong ${\displaystyle {\mathcal {C}}\!:\{x^{\mu }(\lambda ),\lambda \in I\}}$, vectơ tiếp xúc ${\displaystyle {\boldsymbol {V}}_{P}}$ tại điểm P dọc cung ${\displaystyle {\mathcal {C}}}$ được định nghĩa là tập hợp gồm bốn tọa độ

${\displaystyle V_{P}^{\mu }:=\left.{\frac {dx^{\mu }}{d\lambda }}\right|_{P}}$

(15)

Chú ý rằng tại mỗi điểm P chỉ có duy nhất một vectơ tiếp xúc với đường cong và thậm chí hai đường cong có thể có chung một vectơ tiếp tuyến tại điểm chung P, và hai đường này sẽ có thể có một số điểm chung ở một số nơi (hai đường khác nhau) hoặc hoàn toàn đồng nhất giống nhau. Vì điểm P là bất kỳ, có thể viết biểu thức tổng quát cho định nghĩa của vectơ tiếp xúc ${\displaystyle {\boldsymbol {V}}}$ cho đường cong ${\displaystyle {\mathcal {C}}}$ là

${\displaystyle V^{\mu }:={\frac {dx^{\mu }}{d\lambda }}}$

(16)

Chúng ta nên phân biệt giữa vectơ là đối tượng hình học, viết là ${\displaystyle {\boldsymbol {V}}}$, và cách biểu diễn nó trong một hệ tọa độ cụ thể, mà trong trường hợp này chúng ta nói đến các thành phần tọa độ của nó ${\displaystyle V^{\mu }}$. Sự quan trọng của biểu thức (16) là nó cho phép chúng ta có khả năng định nghĩa một đại lượng hình học theo các tính chất của phép biến đổi đối với nó dưới ảnh hưởng của sự thay đổi hệ tọa độ. Quả vậy, chúng ta xét một hệ tọa độ mới ${\displaystyle \{x^{\mu '}\}}$ và sử dụng biểu thức (2) để tính toán các thành phần tọa độ của cùng một vectơ tiếp xúc ${\displaystyle {\boldsymbol {V}}}$ đối với hệ tọa độ mới này

${\displaystyle V^{\mu '}:={\frac {dx^{\mu '}}{d\lambda }}=\sum _{\mu =0}^{3}{\dfrac {\partial {x^{\mu '}}}{\partial {x^{\mu }}}}{\frac {dx^{\mu }}{d\lambda }}=\sum _{\mu =0}^{3}{\dfrac {\partial {x^{\mu '}}}{\partial {x^{\mu }}}}V^{\mu }}$

(17)

với phương trình thứ hai đã áp dụng định nghĩa của vi phân

${\displaystyle dx^{\mu '}=\sum _{\mu =0}^{3}{\dfrac {\partial {x^{\mu '}}}{\partial {x^{\mu }}}}dx^{\mu }}$

(18)

và phương trình cuối cùng (17) có được từ định nghĩa của (16).

Bởi vì cách đặt ký hiệu tốt rất quan trọng và điều này càng có ý nghĩa đặc biệt trong thuyết tương đối rộng, đầu tiên chúng ta có thể viết gọn lại (17) bằng cách áp dụng ký hiệu quy ước tổng do Einstein đặt ra, mà khi ta gặp một chỉ số xuất hiện hai lần điều này sẽ hàm ý việc tính tổng giữa các chỉ số từ 0 đến 3, và thứ hai chúng ta có thể áp dụng cách viết rút ngắn hơn nhờ phương trình (5) cho phép biến đổi ma trận, tức là

${\displaystyle V^{\mu '}=\Lambda ^{\mu '}{}_{\mu }V^{\mu }}$

(19)

Biểu thức (19) cần được giải thích rõ hơn, đầu tiên đó là chỉ số ${\displaystyle \mu }$ là chỉ số được tính tổng (hay chỉ số rút gọn-contraction) tức là nó xuất hiện một lần với vai trò là chỉ số trên (phản biến-contravariance) trong ${\displaystyle V^{\mu }}$ và một lần với vai trò là chỉ số dưới (hiệp biến-covariance) trong ${\displaystyle \Lambda ^{\mu '}{}_{\mu }}$. Chỉ số này còn được gọi là chỉ số câm (dummy) để phân biệt với chỉ số tự do ${\displaystyle \mu '}$ xuất hiện như là một chỉ số không thể thu gọn được ở cả hai vế của phương trình tenxơ (19). Bằng cách kiểm tra số lượng các chỉ số tự do có ở hai vế của phương trình là cách đơn giản nhất, ít nhất về mặt toán học, đó là phương trình tenxơ đã đúng hay chưa (và có thể có nhiều lý do để phương trình chưa đúng).

Phương trình (19) là rất tổng quát và biểu diễn quy tắc biến đổi cho các vectơ phản biến^[5]. Về cơ bản, bốn phương trình trong (19) cho chúng ta cách tính các thành phần tọa độ của vectơ ${\displaystyle \mathbf {V} }$ trong hệ tọa độ ${\displaystyle \{x^{\mu '}\}}$ một khi chúng ta biết các thành phần của nó trong hệ tọa độ ${\displaystyle \{x^{\mu }\}}$.

Chúng ta có thể mở rộng biểu thức (19) cho trường hợp biến đổi tọa độ tổ hợp, tức là khi xét hai hệ tọa độ: biến đổi hệ tọa độ thứ nhất từ hệ ${\displaystyle \{x^{\mu }\}}$ thành ${\displaystyle \{x^{\mu '}\}}$ và sau đó chuyển sang ${\displaystyle \{x^{\mu ''}\}}$ hay

${\displaystyle \{x^{\mu }\}\rightarrow \{x^{\mu '}\}\rightarrow \{x^{\mu ''}\}}$

(20)

và coi đó như là một lần biến đổi

${\displaystyle \{x^{\mu }\}\rightarrow \{x^{\mu ''}\}}$

(21)

do vậy vectơ (phản biến) sẽ biến đổi theo quy tắc

${\displaystyle V^{\mu ''}=\Lambda ^{\mu ''}{}_{\mu '}V^{\mu '}=\Lambda ^{\mu ''}{}_{\mu '}\Lambda ^{\mu '}{}_{\mu }V^{\mu }=\Lambda ^{\mu ''}{}_{\mu }V^{\mu }}$

(22)

Như đã nói ở phần trước, chúng ta có thể viết ra phép biển đổi ngược của (1.19) là

${\displaystyle V^{\mu }=\Lambda ^{\mu }{}_{\mu '}V^{\mu '}}$

(23)

Bốn phương trình (23) cho chúng ta cách tính thành phần tọa độ của vec tơ ${\displaystyle \mathbf {V} }$ trong hệ ${\displaystyle \{x^{\mu }\}}$ một khi đã biết các thành phần của nó trong hệ ${\displaystyle \{x^{\mu '}\}}$. Rõ ràng là hai ma trận biến đổi của hai phép biến đổi ngược là ma trận nghịch đảo của nhau, hay

${\displaystyle \Lambda ^{\mu '}{}_{\mu }\Lambda ^{\mu }{}_{\nu '}=\delta _{\nu '}^{\mu '}={\begin{cases}1,&{\mbox{khi }}\mu '=\nu '\\0,&{\mbox{khi }}\mu '\neq \nu '\end{cases}}}$

(24)

Điều này cũng đúng cho phép biến đổi ngược lại

${\displaystyle \Lambda ^{\mu }{}_{\mu '}\Lambda ^{\mu '}{}_{\nu }=\delta _{\nu }^{\mu }={\begin{cases}1,&{\mbox{khi }}\mu =\nu \\0,&{\mbox{khi }}\mu \neq \nu \end{cases}}}$

(25)

Chú ý rằng cả hai phương trình (24) và (25) là tương đương với Jacobian của biến đổi khác 0,

${\displaystyle det\left(\Lambda ^{\mu '}{}_{\mu }\right)\neq 0;det\left(\Lambda ^{\mu }{}_{\mu '}\right)\neq 0}$

(26)

Đại lượng ${\displaystyle \delta _{\nu }^{\mu }}$ được gọi là ký hiệu Kronecker.

Ở phần này, chúng ta đã giới thiệu một tập hợp tổng quát chứa các điểm được liên hệ với nhau thông qua một tham số, hay đường cong trong đa tạp, sau đó nêu ra định nghĩa khái niệm vectơ tiếp xúc tại một điểm P và học được cách biểu diễn đại lượng hình học này biến đổi như thế nào dưới những hệ tọa độ khác nhau. Điều này dẫn chúng ta tới một khái niệm tổng quát hơn đó là không gian tiếp xúc của đa tạp ${\displaystyle {\mathcal {M}}}$ tại điểm P: đó là không gian chứa mọi vectơ phản biến tại P.

Gradien của hàm số[sửa | sửa mã nguồn]

Một vec tơ bất kỳ có thể được xây dựng dựa trên khái niệm đường cong. Chúng ta có thể thấy điều này bằng cách áp dụng định nghĩa (11) của đường cong ${\displaystyle {\mathcal {C}}}$ trong đa tạp và giới thiệu ra hàm vô hướng ${\displaystyle \phi }$, một hàm giá trị thực ánh xạ điểm P bất kỳ có tọa độ ${\displaystyle x^{\mu }(\lambda )}$ trong ${\displaystyle {\mathcal {M}}}$ vào một số thực ${\displaystyle \phi (x^{m}u(\lambda )){\Big |}_{P}}$. Bây giờ chúng ta có thể tính được hàm thực này biến đổi như thế nào dọc đường cong ${\displaystyle {\mathcal {C}}}$ bằng^[6]

${\displaystyle {\frac {d\phi }{d\lambda }}={\dfrac {\partial \phi }{\partial x^{\mu }}}{\frac {dx^{\mu }}{d\lambda }}={\dfrac {\partial \phi }{\partial x^{\mu }}}V^{\mu }=U_{\mu }V^{\mu }}$

(27)

Phương trình thứ hai trong phương trình (27) chỉ đơn giản là định nghĩa của vectơ tiếp xúc đã gặp ở (16), trong khi ở phương trình thứ ba là định nghĩa của gradien của hàm số ${\displaystyle \phi }$

${\displaystyle U_{\mu }:={\dfrac {\partial \phi }{\partial x^{\mu }}}=({\tilde {d}}\phi )_{\mu }}$

(28)

với chỉ số tự do phải là chỉ số nằm ở dưới (tức là hiệp biến) và đây là đặc điểm phân biệt với vectơ ${\displaystyle U^{\mu }}$.

Để hiểu tốt hơn tại sao chỉ số trong ${\displaystyle U_{\mu }}$ phải ở dưới, chúng ta có thể nghiên cứu cách đối tượng hình học này hành xử dưới một phép biến đổi tọa độ và làm rõ ý nghĩa của nó hơn. Một lần nữa, nếu ${\displaystyle U_{\mu }}$ là thành phần của đối tượng này trong hệ tọa độ ${\displaystyle \{x^{\mu }\}}$ thì thành phần của nó trong ${\displaystyle \{x^{\mu '}\}}$ là

${\displaystyle U_{\mu '}:={\dfrac {\partial \phi }{\partial x^{\mu '}}}={\dfrac {\partial \phi }{\partial x^{\mu }}}{\dfrac {\partial x^{\mu }}{\partial x^{\mu '}}}=U_{\mu }{\dfrac {\partial x^{\mu }}{\partial x^{\mu '}}}}$

(29)

Hay nói cách khác, quy tắc biến đổi cho gradien của hàm số ${\displaystyle \phi }$ là

${\displaystyle ({\tilde {d}}\phi )_{\mu '}={\dfrac {\partial x^{\mu }}{\partial x^{\mu '}}}({\tilde {d}}\phi )_{\mu }}$

(30)

và có thể được sử dụng làm định nghĩa cho khái niệm vectơ hiệp biến (covariant vector).

Chú ý rằng biến đổi (30) là biến đổi ngược của quy tắc đã gặp cho các thành phần của vectơ [xem phương trình (19)]. Lý do cho điều này đến từ thực tế rằng vectơ phản biến và vectơ hiệp biến là đại lượng đối ngẫu của nhau, do đó không gian chứa mọi vectơ hiệp biến là không gian đối ngẫu của không gian tiếp tuyến mà chúng ta đã gặp ở phần trước.^[7] Bởi vì đây là một kết quả quan trọng và mối liên hệ sâu sắc giữa vectơ hiệp biến và vectơ phản biến sẽ được trình bày rõ ở phần sau. Như đối với vectơ phản biến, chúng ta có thể đưa ra biến đổi ngược cho vectơ hiệp biến và dễ dàng thu được

${\displaystyle ({\tilde {d}}\phi )_{\mu }={\dfrac {\partial x^{\mu '}}{\partial x^{\mu }}}({\tilde {d}}\phi )_{\mu '}}$

(31)

Người đọc thận trọng có thể tự hỏi tại sao chúng ta không viết (30) như sau

${\displaystyle ({\tilde {d}}\phi )_{\mu '}=\Lambda ^{\mu }{}_{\mu '}({\tilde {d}}\phi )_{\mu }}$

(32)

và tại sao không viết (31) như sau

${\displaystyle ({\tilde {d}}\phi )_{\mu }=\Lambda ^{\mu '}{}_{\mu }({\tilde {d}}\phi )_{\mu '}}$

(33)

Lý do đằng sau sự lựa chọn này là ở cách ký hiệu ma trận theo cách viết trong (32) và (33) có thể sẽ gây ra sự nhầm lẫn một khi chúng ta coi ${\displaystyle \Lambda _{\mu '}^{\mu }}$ giống như ở trong phương trình (23). Điều này sẽ trở lên rõ ràng nếu chúng ta quay trở lại ví dụ về biến đổi tọa độ miêu tả ở trong phần Hệ tọa độ. Quả thực, khi chúng ta biến đổi gradien của một vô hướng từ tọa độ ${\displaystyle (x,y)}$ sang ${\displaystyle (r,\theta )}$, ma trận đúng viết trong (32) mà nhân với vectơ cột ${\displaystyle {\tilde {d}}\phi )_{\mu }}$ phải là

${\displaystyle \Lambda ^{i'}{}_{j}=\left({\begin{array}{rr}{\dfrac {\partial x}{\partial r}}&{\dfrac {\partial y}{\partial r}}\\{\dfrac {\partial x}{\partial \theta }}&{\dfrac {\partial y}{\partial \theta }}\end{array}}\right)}$

(34)

mà chính là ma trận chuyển vị của ma trận được định nghĩa trong (10).

Ở những phần sau, chúng ta sẽ sử dụng ký hiệu ${\displaystyle \Lambda ^{\mu '}{}_{\mu }}$ đại diện cho ${\displaystyle \partial x^{\mu '}/\partial x^{\mu }}$ và ${\displaystyle \Lambda ^{\mu }{}_{\mu '}}$ đại diện cho ${\displaystyle \partial x^{\mu }/\partial x^{\mu '}}$.

Ý nghĩa hình học của vectơ phản biến và vectơ hiệp biến[sửa | sửa mã nguồn]

Chúng ta có thể kết hợp các định nghĩa trên đây để đi đến một miêu tả thống nhất về vectơ phản biến và vectơ hiệp biến. Đặc biệt, chúng ta có thể sử dụng định nghĩa gradien dọc một đường cong (27) và viết lại thành

${\displaystyle {\frac {d\phi }{d\lambda }}={\frac {dx^{\mu }}{d\lambda }}{\dfrac {\partial \phi }{\partial x^{\mu }}}=V^{\mu }({\tilde {d}}\phi )_{\mu }}$

(35)

do đó vectơ phản biến ${\displaystyle \mathbf {V} }$ có thể được coi như là một đối tượng hình học tiếp tuyến với đường cong có tham số ${\displaystyle \lambda }$ và đo tỉ số ${\displaystyle {d\phi }/{d\lambda }}$ cho một hàm vô hướng bất kỳ ${\displaystyle \phi }$ dọc đường cong. Theo cách này, có thể coi vectơ là đại lượng độc lập với hệ tọa độ, và xác định lên, ít nhất trong một miền lân cận nhất định, đường cong mà nó tiếp xúc. Thành phần phản biến ${\displaystyle V^{\mu }}$ của nó cho phép đo sự thay đổi của hệ tọa độ dọc theo đường cong đó và những thứ này có mối liên hệ chặt với cách lựa chọn hệ tọa độ; một hệ tọa độ khác sẽ dẫn tới những thành phần tọa độ khác, cũng như hàm gradien ${\displaystyle ({\tilde {d}}\phi )_{\mu }}$ khác.

Tất nhiên, chúng ta có thể thực hiện mà không cần hàm vô hướng ${\displaystyle \phi }$ trong (1.35) và coi vectơ như là một đối tượng xác định bằng

${\displaystyle \mathbf {V} :={\dfrac {d}{d\lambda }}=V^{\mu }{\dfrac {\boldsymbol {\partial }}{{\boldsymbol {\partial x}}^{\mu }}}=V^{\mu }\mathbf {e} _{\mu }}$

(36)

mà chúng ta đưa ra ký hiệu

${\displaystyle \mathbf {e} _{\mu }:={\dfrac {\boldsymbol {\partial }}{{\boldsymbol {\partial x}}^{\mu }}}={\boldsymbol {\partial }}_{\mu }}$

(37)

để chỉ bốn vectơ cơ sở ${\displaystyle \{e_{\mu }\}}$ dọc theo hướng xác định bởi tọa độ ${\displaystyle \{x_{\mu }\}}$^[9] Những cơ sở vectơ này, mà có liên hệ chặt với hệ tọa độ đang áp dụng, được gọi là tọa độ cơ sở. Theo cách này, biểu thức (36) nói một cách đơn giản rằng ${\displaystyle \mathbf {V} }$ là tổ hợp của các thành phần phản biến ${\displaystyle V^{\mu }}$ dọc theo hướng tọa độ.

Định nghĩa vectơ theo phương trình (36) mang bản chất hình học của vectơ và có vẻ rất khác thường. Nhưng thực ra nếu xem xét kỹ, khi coi đa tạp ba chiều đi kèm với đạo hàm theo hướng (directional derivative) ${\displaystyle \{{\boldsymbol {\partial }}/{{\boldsymbol {\partial x}}^{i}}\}}$ với cơ sở vectơ ${\displaystyle \{e_{i}\}}$ của giải tích vectơ cổ điển, khi đó rõ ràng rằng vectơ trong (36) lại được biểu diễn trùng với hệ ba vectơ ba chiều, tức là

${\displaystyle {\begin{aligned}{\overrightarrow {\mathbf {V} }}=V^{i}{\overrightarrow {\mathbf {e} }}_{i}&=V^{x}{\overrightarrow {\mathbf {e} }}_{x}+V^{y}{\overrightarrow {\mathbf {e} }}_{y}+V^{z}{\overrightarrow {\mathbf {e} }}_{z}\\&=V^{r}{\overrightarrow {\mathbf {e} }}_{r}+V^{\theta }{\overrightarrow {\mathbf {e} }}_{\theta }+V^{\phi }{\overrightarrow {\mathbf {e} }}_{\phi }=...\\\end{aligned}}}$

(38)

khi ${\displaystyle {\overrightarrow {\mathbf {V} }}}$ được biểu diễn trong hệ tọa độ DeCartes (phương trình thứ hai) và trong hệ tọa độ cầu (phương trình thứ ba) hoặc trong bất kỳ cơ sở tọa độ nào. Cách nhìn mới về vec tơ này cũng hữu ích khi mở ra cách nhìn mới về đối vectơ hay một dạng một (covector, one form). Quả vậy, chúng ta có thể quay trở lại định nghĩa trong (35) và xét tới vectơ hiệp biến ${\displaystyle {\boldsymbol {\tilde {d}}}}$ như là một toán tử ${\displaystyle {\boldsymbol {{\tilde {d}}(.)}}}$ tác dụng lên vectơ sao cho khi áp dụng đối với vectơ ${\displaystyle \mathbf {V} }$ nó trả lại một số thực,^[10] nghĩa là

${\displaystyle {\boldsymbol {{\tilde {d}}(V)}}=V^{\mu }d_{\mu }}$

(39)

Khi coi là một toán tử tác dụng lên vectơ, đối vec tơ là một toán tử tuyến tính tức là

${\displaystyle {\boldsymbol {\tilde {d}}}=a{\boldsymbol {\tilde {p}}}+b{\boldsymbol {\tilde {q}}}\Rightarrow {\boldsymbol {\tilde {d}}}({\boldsymbol {V}})=a{\boldsymbol {\tilde {p}}}({\boldsymbol {V}})+b{\boldsymbol {\tilde {q}}}({\boldsymbol {V}})}$

(40)

với a, b là các hệ số hằng số. Ngoài ra, nó còn tuân theo luật phân phối

${\displaystyle {\boldsymbol {\tilde {d}}}(a{\boldsymbol {V}}+b{\boldsymbol {U}})=a{\boldsymbol {\tilde {d}}}({\boldsymbol {V}})+b{\boldsymbol {\tilde {d}}}({\boldsymbol {U}})}$

(41)

Cách giải thích hình học này đã thực sự thống nhất các khái niệm vectơ và đối vectơ (1-dạng, 1-form). Theo cách này, một vec tơ ${\displaystyle \mathbf {V} }$ xác định lên đường cong mà nó tiếp tuyến với, trong dạng một ${\displaystyle {\tilde {d}}}$ xác định gradien của một hàm vô hướng dọc cùng cung đó. Hơn nữa, dạng một tác dụng lên vectơ tạo ra một số độc lập với tọa độ và do vậy là bất biến tương đối tính. Tính chất quan trọng này được chứng minh bắt đầu bằng định nghĩa (39) khi viết trong hệ tọa độ mới ${\displaystyle \{x^{\mu '}\}}$

${\displaystyle {\begin{aligned}{\boldsymbol {{\tilde {d}}(V)}}=V^{\mu '}d_{\mu '}&=(\Lambda ^{\mu '}{}_{\nu }V^{\nu })(\Lambda ^{\mu }{}_{\mu '}d_{\mu })\\&=\Lambda ^{\mu '}{}_{\nu }\Lambda ^{\mu }{}_{\mu '}V^{\nu }d_{\mu }\\&=\delta ^{\mu }{}_{\nu }V^{\nu }d_{\mu }=V^{\mu }d_{\mu }\\\end{aligned}}}$

(42)

Tính chất bất biến này cũng áp dụng cho định nghĩa (36) của vectơ và cho phép chúng ta suy ra quy tắc biến đổi của cơ sở vectơ

${\displaystyle {\begin{aligned}{\boldsymbol {V}}=V^{\mu '}{\boldsymbol {e}}_{\mu '}&=V^{\mu }{\boldsymbol {e}}_{\mu }\\&=\Lambda ^{\mu }{}_{\nu '}V^{\nu '}{\boldsymbol {e}}_{\mu }=\Lambda ^{\mu }{}_{\mu '}V^{\mu '}{\boldsymbol {e}}_{\mu }\\\end{aligned}}}$

(43)

do đó, gộp các thành phần của vectơ ${\displaystyle \mathbf {V} }$ ta được

${\displaystyle V^{\mu '}({\boldsymbol {e}}_{\mu '}-\Lambda ^{\mu }{}_{\mu '}{\boldsymbol {e}}_{\mu })=0,}$

(44)

Vì thế, đối với mọi vectơ không tầm thường ta có

${\displaystyle {\boldsymbol {e}}_{\mu '}=\Lambda ^{\mu }{}_{\mu '}{\boldsymbol {e}}_{\mu }}$

(45)

Mặc dù biểu thức (45) không phải là phương trình biến đổi cho thành phần tọa độ, nhưng chúng ta nhận ra ngay lập tức sự tương tự giữa (45) và quy tắc biến đổi cho thành phần của đối vectơ trong (32). Vì vậy có thể nói rằng cơ sở vectơ biến đổi theo quy tắc giống như các thành phần của đối vectơ biến đổi và theo "cách ngược lại" với thành phần của vectơ. Chú ý rằng chữ "ngược" trong dấu hai phẩy vì nếu ta đọc biến đổi vectơ cơ sở trong (45) như là biểu diễn ma trận của sự thay đổi cơ sở, thì biểu diễn ma trận tương ứng trong (19) chấp nhận nghịch đảo của ma trận chuyển vị sử dụng trong (45) chứ không phải nghịch đảo của ma trận này (xem ở phần Gradien của hàm số).

Cuối cùng, khi đã giới thiệu định nghĩa cơ sở vectơ, sẽ tự nhiên khi đặt ra câu hỏi về định nghĩa cơ sở của đối vectơ do vectơ và đối vectơ (hay dạng một) là những đại lượng đối ngẫu, nghĩa là

${\displaystyle {\boldsymbol {\tilde {\omega }}}^{\mu }({\boldsymbol {e}}_{\nu })=\delta _{\nu }^{\mu }}$

(46)

do đó một cơ sở vectơ ${\displaystyle \{{\boldsymbol {e}}_{\nu }\}}$ sinh ra một cơ sở đối vectơ ${\displaystyle \{{\boldsymbol {{\tilde {\omega }}^{\mu }}}\}}$, và bất kỳ một đối vectơ ${\displaystyle {\boldsymbol {\tilde {p}}}}$ có thể biểu diễn theo các thành phần của nó

${\displaystyle {\boldsymbol {\tilde {p}}}=p_{\mu }{\boldsymbol {\tilde {\omega }}}^{\mu }}$

(47)

Để chứng minh (46) là đúng, chúng ta có thể sử dụng (36) và (47) để nhận được

${\displaystyle {\begin{aligned}p_{\mu }V^{\mu }={\boldsymbol {{\tilde {p}}(V)}}&=p_{\mu }{\boldsymbol {\tilde {\omega }}}^{\mu }({\boldsymbol {V}})\\&=p_{\mu }{\boldsymbol {\tilde {\omega }}}^{\mu }(V^{\nu }{\boldsymbol {e}}_{\nu })\\&=p_{\mu }V^{\nu }{\boldsymbol {\tilde {\omega }}}^{\mu }({\boldsymbol {e}}_{\nu })=p_{\mu }V^{\nu }\delta _{\nu }^{\mu }.\\\end{aligned}}}$

(48)

Tenxơ[sửa | sửa mã nguồn]

Định nghĩa của vectơ và đối vectơ đã giới thiệu ở phần trước là cơ sở cho nội dung của phần này. Chúng đã được giới thiệu để xác định các đối tượng hình học độc lập với bất kỳ hệ tọa độ nào và chúng ta đã học được rằng khi đưa ra một hệ tọa độ và chuyển đổi sang hệ tọa độ khác, các vectơ phản biến và vectơ hiệp biến biến đổi theo những quy tắc đơn giản trong (19) và (30).

Có ít nhất hai khía cạnh của vec tơ (hoặc đối với vectơ phản biến hoặc hiệp biến) mà khá rõ ràng. Thứ nhất đó là chúng ta không nhất thiết phải giới hạn định nghĩa vectơ tại một điểm. Mặt khác chúng ta có thể nghĩ tới toàn bộ miền của đa tạp ${\displaystyle {\mathcal {M}}}$ và thông qua một hàm trơn khả vi chúng ta gắn mỗi vectơ tại mỗi điểm của miền này, qua đó định nghĩa lên trường vectơ

${\displaystyle f:\{P\in {\mathcal {M}}\longrightarrow V^{\mu }(P)\},\quad \quad g:\{P\in {\mathcal {M}}\longrightarrow U_{\mu }(P)\},}$

(49)

với ${\displaystyle V^{\mu }(P),U_{\mu }(P)}$ là giá trị của trường tại điểm P. Hơn nữa, trường vectơ được nói là khả vi nếu các thành phần của nó là những hàm tọa độ khả vi trong mọi hệ tọa độ. Khía cạnh thứ hai đó là vectơ chỉ là thành phần đơn giản nhất của một lớp đối tượng hình học tổng quát hơn gọi là tenxơ. Cũng như đối vectơ hiệp biến và vectơ phản biến, ten xơ có thể coi như là những đối tượng hình học mà được xác định hoàn toàn theo những tính chất dưới một phép biến đổi tọa độ.

Nhất quán với cách tiếp cận này, chúng ta định nghĩa một tenxơ phản biến hạng hai là một đối tượng hình học ${\displaystyle \mathbb {T} }$, mà các thành phần biến đổi tuân theo quy tắc sau khi chuyển từ hệ tọa độ ${\displaystyle \{x^{\mu }\}}$ sang hệ mới ${\displaystyle \{x^{\mu '}\}}$^[11]

${\displaystyle T^{\mu '\nu '}={\dfrac {\partial x^{\mu '}}{\partial x^{\mu }}}{\dfrac {\partial x^{\nu '}}{\partial x^{\nu }}}T^{\mu \nu }=\Lambda ^{\mu '}{}_{\mu }\Lambda ^{\nu '}{}_{\nu }T^{\mu \nu }}$

(50)

Tương tự chúng ta có thể định nghĩa tenxơ hiệp biến hạng hai là một đối tượng hình học ${\displaystyle \mathbb {T} }$, mà các thành phần biến đổi tuân theo quy tắc sau khi chuyển từ hệ tọa độ ${\displaystyle \{x^{\mu }\}}$ sang hệ ${\displaystyle \{x^{\mu '}\}}$^[12]

${\displaystyle T_{\mu '\nu '}={\dfrac {\partial x^{\mu }}{\partial x^{\mu '}}}{\dfrac {\partial x^{\nu }}{\partial x^{\nu '}}}T_{\mu \nu }=\Lambda ^{\mu }{}_{\mu '}\Lambda ^{\nu }{}_{\nu '}T_{\mu \nu }}$

(51)

Nếu hệ tọa độ là thông thường, cả hai biểu thức (50) và (51) sẽ thừa nhận phép biến đổi ngược và có thể suy ra trực tiếp dựa trên các biểu thức (23) và (31). Một cách tự nhiên, chúng ta có thể định nghĩa tenxơ hỗn hợp là một đối tượng hình học có cả thành phần hiệp biến và phản biến. Do vậy, ví dụ, chúng ta có thể định nghĩa tenxơ hỗn hợp loại (4,2) (tức là nó có bốn thành phần phản biến và hai thành phần hiệp biến) ${\displaystyle R^{\alpha \beta \gamma \delta }{}_{\mu \nu }}$ mà quy tắc biến đổi khi chuyển từ hệ tọa độ ${\displaystyle \{x^{\mu }\}}$ sang hệ ${\displaystyle \{x^{\mu '}\}}$ là^[13]

${\displaystyle R^{\alpha '\beta '\gamma '\delta '}{}_{\mu '\nu '}=\Lambda ^{\alpha '}{}_{\alpha }\Lambda ^{\beta '}{}_{\beta }\Lambda ^{\gamma '}{}_{\gamma }\Lambda ^{\delta '}{}_{\delta }\Lambda ^{\mu }{}_{\mu '}\Lambda ^{\nu }{}_{\nu '}R^{\alpha \beta \gamma \delta }{}_{\mu \nu }}$

(52)

và biến đổi ngược sẽ là

${\displaystyle R^{\alpha \beta \gamma \delta }{}_{\mu \nu }=\Lambda ^{\alpha }{}_{\alpha '}\Lambda ^{\beta }{}_{\beta '}\Lambda ^{\gamma }{}_{\gamma '}\Lambda ^{\delta }{}_{\delta '}\Lambda ^{\mu '}{}_{\mu }\Lambda ^{\nu '}{}_{\nu }R^{\alpha '\beta '\gamma '\delta '}{}_{\mu '\nu '}}$

(53)

Từ hai ví dụ trên sẽ không khó để hình dung ra cách xây dựng một tenxơ với số thành phần phản biến và hiệp biến là bất kỳ. Chúng ta có thể xây dựng lên không gian vectơ ${\displaystyle \mathbf {V} ^{m}{}_{n}}$ là tập hợp mọi tenxơ kiểu (m, n), ví dụ ${\displaystyle R^{\alpha \beta \gamma \delta }{}_{\mu \nu }\in \mathbf {V} ^{4}{}_{2}}$.

Giờ đây chúng ta có thể coi vectơ và đối vectơ như là những tenxơ kiểu đặc biệt (lần lượt là kiểu (1, 0) và (0, 1)). Viết tenxơ theo các cơ sở vectơ (36) và cơ sở đối vectơ (47) để biểu diễn một tenxơ hỗn hợp như là đối tượng hình học độc lập với hệ tọa độ. Ví dụ đối với tenxơ hỗn hợp loại (1, 1) là

${\displaystyle \mathbf {R} =R^{\mu }{}_{\nu }\mathbf {e} _{\mu }\otimes {\mathbf {\tilde {\omega }} }^{\nu }}$

(54)

với ký hiệu ${\displaystyle \otimes }$ là tích tenxơ. Chú ý rằng tích này không có tính giao hoán, tức là ${\displaystyle \mathbf {e} _{\mu }\otimes {\mathbf {\tilde {\omega }} }^{\nu }\neq {\mathbf {\tilde {\omega }} }^{\nu }\otimes \mathbf {e} _{\mu }}$. Do vậy, hai tenxơ ${\displaystyle \mathbf {R} =R^{\mu }{}_{\nu }\mathbf {e} _{\mu }\otimes {\mathbf {\tilde {\omega }} }^{\nu }}$ và ${\displaystyle \mathbf {\tilde {R}} ={\tilde {R}}_{\nu }{}^{\mu }{\mathbf {\tilde {\omega }} }^{\nu }\otimes \mathbf {e} _{\mu }}$ là hai tenxơ khác nhau.