Перелік розподілів імовірності

Багато розподілів імовірності, які важливі в теорії або застосуванні, отримали окремі назви.

• Розподіл Бернуллі, яке приймає значення 1 з ймовірністю p та значення 0 з ймовірністю q = 1 − p .
• Розподіл Радемахера, який приймає значення 1 з ймовірністю 1/2 і значення − 1 з ймовірністю 1/2.
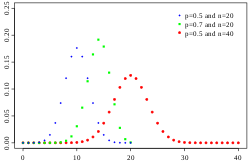
• Біноміальний розподіл, який описує кількість успіхів у серії незалежних експериментів «так/ні» з однаковою ймовірністю успіху.
• Бета-біноміальний розподіл, який описує кількість успіхів у серії незалежних експериментів Так/Ні з неоднорідністю ймовірності успіху.
• Вироджений розподіл при x ₀, де X точно прийме значення x ₀ . Це не виглядає випадковим, але задовольняє визначенню випадкової величини . Це корисно, оскільки ставить детерміновані змінні та випадкові змінні в один формалізм.
• Дискретний рівномірний розподіл, де всі елементи скінченної множини однаково ймовірні. Це теоретична модель розподілу збалансованої монети, неупередженого кубика, рулетки казино або першої карти добре перемішаної колоди.
• Гіпергеометричний розподіл, який описує число успіхів в перших т у серії п послідовних експериментів Так / Ні, якщо загальне число успіхів відомо. Такий розподіл виникає, коли немає заміни.
• Негативний гіпергеометричний розподіл, який описує кількість спроб, необхідних для досягнення n -го успіху в серії експериментів «так/ні» без заміни.
• Біноміальний розподіл Пуассона, який описує кількість успіхів у серії незалежних експериментів Так/Ні з різною ймовірністю успіху.
• Нецентральний гіпергеометричний розподіл Фішера
• Нецентральний гіпергеометричний розподіл Валленіуса
• Закон Бенфорда, який описує частоту першої цифри багатьох природних даних.
• Ідеальні та надійні розподіли солітонів .
• Закон Зіффа або розподіл Зіффа. Дискретний степеневий розподіл, найбільш відомим прикладом якого є опис частоти слів в англійській мові.
• Закон Зіпфа – Мандельброта - це дискретний степеневий розподіл, який є узагальненням розподілу Зіпфа .

• Бета -негативний біноміальний розподіл
• Розподіл Больцмана, дискретний розподіл, важливий у статистичній фізиці, який описує ймовірності різних рівнів дискретної енергії системи в тепловій рівновазі . Він має безперервний аналог. Особливі випадки включають:
  • Розподіл Гіббса
  • Розподіл Максвелла – Больцмана
• Розподіл Бореля
• Розширений негативний біноміальний розподіл
• Узагальнений розподіл логарифмічних рядів
• Розподіл Гаусса – Кузьміна
• Геометричний розподіл - дискретний розподіл, який описує кількість спроб, необхідних для досягнення першого успіху в серії незалежних випробувань Бернуллі, або, альтернативно, лише кількість втрат до першого успіху (тобто на одну спробу менше).
• Логарифмічний (послідовний) розподіл
• Негативний біноміальний розподіл або розподіл Паскаля, узагальнення геометричного розподілу до n -го успіху.
• Дискретний складний розподіл Пуассона
• Параболічний фрактальний розподіл
• Розподіл Пуассона, який описує дуже велику кількість індивідуальних малоймовірних подій, що відбуваються в певному часовому інтервалі. З цим розподілом пов'язана низка інших розподілів: зміщений Пуассон, гіперпуассон, загальний біноміал Пуассона та розподіли типу Пуассона.
  • Розподіл Конвея – Максвелла – Пуассона, двопараметричне розширення розподілу Пуассона з регульованою швидкістю спаду.
  • Обмежений нулем розподіл Пуассона для процесів, у яких нульовий рахунок не спостерігається
• Розподіл Полі – Еггенбергера
• Розподіл Скеллама, розподіл різниці між двома незалежними розподіленими Пуассоном випадковими величинами.
• Косий еліптичний розподіл
• Розподіл Юля – Саймона
• Розподіл дзета, що має застосування у прикладній статистиці та статистичній механіці, і, можливо, може бути корисним для теоретиків чисел. Це розподіл Zipf для нескінченної кількості елементів.