Задача Вебера

Завдання Вебера — одна з найвідоміших задач розміщення виробництва. Названа на честь німецького економіста Альфреда Вебера. У задачі потрібно знайти точку на площині, яка мінімізує суму цін перевезень з цієї точки в n точок споживання, де для різних точок споживання призначається ціна перевезення на одиницю відстані.
Задача Вебера узагальнює пошук геометричної медіани, для якої ціни перевезень вважаються рівними для всіх точок споживання, і задачу знаходження точки Ферма, геометричної медіани трьох точок. З цієї причини задачу іноді називають задачею Ферма — Вебера, хоча таку ж назву використовують і для задачі знаходження незваженої геометричної медіани. Задача Вебера, у свою чергу, узагальнюється задачею притягання-відштовхування, яка дозволяє від'ємні ціни, так що для деяких точок більша відстань краща.
Визначення та історія задач Ферма, Вебера та притягання–відштовхування[ред. | ред. код]
| Задача Ферма | Задача Вебера | Задача притягання-відштовхування | |
|---|---|---|---|
| Сформульована | Ферма (до 1640) | Сімпсон (1750) | Тельє (1985) |
| Геометричне розв'язання задачі трикутника | Торрічеллі (1645) | Сімпсон (1750) | Тельє (2013) |
| Пряме чисельне розв'язання задачі трикутника | Тельє (1972) | Тельє (1972) | Тельє (1985) |
| Ітеративне чисельне розв'язання задачі | Кун і Куен (1962) | Кун і Куен (1962) | Чен, Хансен, Жомар та Туй (1992) |
Задача Ферма для трикутника полягає у знаходженні такої точки D, що сума відстаней від неї до кожної трьох точок A, B і C мінімальна. Задачу сформулював знаменитий французький математик П'єр Ферма до 1640 року. Задачу можна розглядати як початок задачі розміщення виробництва. Торрічеллі знайшов геометричне розв'язання задачі близько 1645 року, але прямого чисельного розв'язання не існувало ще більше 325 років. Кун і Куен[1] знайшли ітеративне розв'язання загальної задачі Ферма 1962 року, а 1972 року Люк-Норманд Тельє[en][2] знайшов пряме чисельне (тригонометричне) розв'язання трикутної задачі Ферма. Розв'язання Куна і Куена придатний для многокутників із більш ніж трьома сторонами, чого не має розв'язання Тельє з причин, пояснених далі.
Задача Вебера для трикутника полягає у знаходженні такої точки D, що сума вартостей перевезення від неї до трьох точок A, B і C мінімальна. Задача Вебера є узагальненням задачі Ферма, оскільки використовує рівні і нерівні сили притягання (див. нижче), тоді як у задачі Ферма сили однакові. Задачу для випадку трикутника вперше сформулював і розв'язав Томас Сімпсон 1750 року[3][4]. Кун і Куен знайшли ітеративне розв'язання 1962 року, а розв'язання Тельє, знайдене 1972 року, застосовне як до задачі Вебера, так і до задачі Ферма. Розв'язання Куна й Куена застосовне до многокутників із більш ніж трьома сторонами.
У найпростішому випадку задача притягання-відштовхування полягає в знаходженні для трьох точок A1, A2 і R такої точки D, що прикладені до неї сили притягання точок A1 і A2 та сила відштовхування точки R компенсують одна одну[5]. Задача узагальнює як задачу Ферма, так і задачу Вебера. Задачу сформулював і розв'язав для трикутника 1985 року Люк-Норманд Тельє[6]. 1992 року Чен, Гансен, Жомар і Туй знайшли розв'язання задачі Тельє для многокутників із більш ніж трьома сторонами.
Геометричне розв'язання Торрічеллі задачі Ферма для трикутника[ред. | ред. код]

Геометричне розв'язання Еванджеліста Торрічеллі задачі Ферма для трикутника спирається на два спостереження:
1. Точка D має оптимальне положення, якщо будь-яке зрушення з цієї точки призводить до збільшення сумарної відстані до точок A, B і C, що означає, що оптимальна точка — це тільки та точка, в якій нескінченно малий зсув у напрямку до однієї з трьох точок дорівнює сумі змін до двох інших точок. Іншими словами, точка D однаково притягується точками A, B та C.
2. В опуклому чотирикутнику, вписаному в коло, протилежні кути в сумі дають 180°. Можна це сформулювати так: якщо розсікти коло хордою AB, отримаємо дуги кола, скажімо, AiB і AjB. Будь-який кут ∠AiB, що спирається на дугу AiB, однаковий для будь-якої точки i, а кут ∠AjB, що спирається на дугу AjB, однаковий для будь-якої точки j. Більш того, кути ∠AiB та ∠AjB в сумі дають 180°.
Можна довести, що з першого спостереження випливає, що в точці оптимуму кути, у вершинах трикутників, що спираються на відрізки AD, BD і CD, повинні дорівнювати 360° / 3 = 120°. З цього Торрічеллі дійшов висновку, що:
1. Якщо з трикутника ABD, кут ∠ADB якого дорівнює 120°, утворено вписаний у коло опуклий чотирикутник ABDE, кут ∠AEB трикутника ABE має дорівнювати (180° − 120°)= 60°;
2. Один зі способів отримання точки D, для якої кут ∠ADB дорівнює 120° — побудувати рівносторонній трикутник ABE (оскільки всі кути рівностороннього трикутника дорівнюють 60°), де точка E розташована поза трикутником ABC, і побудувати коло навколо цього трикутника. Тоді для всіх точок D' описаного навколо трикутника кола, що лежать усередині трикутника, кут ∠AD'B дорівнює 120°;
3. Те саме можна зробити для трикутників ACD і BCD;
4. Це приводить до побудови рівносторонніх трикутників ACF і BCG, де F і G лежать поза трикутником ABC, а також до побудови двох інших кіл навколо цих рівносторонніх трикутників. Всі три кола перетинаються в одній точці D і кути, що спираються на відрізки AD, BD і CD дорівнюватимуть 120°, що доводить оптимальність положення точки.
Геометричне розв'язання Сімпсона задачі Вебера для трикутника[ред. | ред. код]
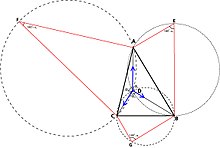
Геометричний розв'язання Сімпсона так званої «задачі Вебера для трикутника» (яку сформулював Томас Сімпсон 1750 року) безпосередньо випливає з розв'язання Торрічеллі. Сімпсон і Вебер підкреслюють факт, що в задачі мінімізації перевезень вигода від наближення до точок споживання A, B чи C залежить від того, що перевозиться і за яку ціну. Отже, вигода від наближення на деяку відстань змінюється і кути ∠ADB, ∠ADC та ∠BDC більше не повинні дорівнювати 120°.
Сімпсон показав, що трикутники ABE, ACF і BCG, що будуються аналогічно розв'язанню Торрічеллі, де E, F і G розташовані поза трикутником ABC, повинні бути пропорційні силам притягання. У разі задачі Ферма трикутники були рівносторонніми, оскільки сили притягання однакові
Розв'язання таке:
1. У трикутнику ABE, що будується, сторона AB пропорційна силі притягання Cw у напрямку до C, сторона AE пропорційна силі притягання Bw у напрямку до B, а сторона BE пропорційна силі притягання Aw у напрямку до A.
2. У трикутнику BCG, що будується, сторона BC пропорційна силі тяжіння Aw у напрямку до A, сторона BG пропорційна силі тяжіння Bw у напрямку до B, а сторона CG пропорційна силі тяжіння Cw у напрямку до C;
3. Оптимальна точка D розташована на перетині двох кіл навколо побудованих трикутників ABE і BCG.
На стороні AC можна побудувати третій трикутник ACF, де F міститься поза трикутником ABC, і навколо цього трикутника можна побудувати третє коло. Це третє коло перетинає два інші кола в тій самій точці D.
Геометричне розв'язання Тельє задачі притягання-відштовхування[ред. | ред. код]
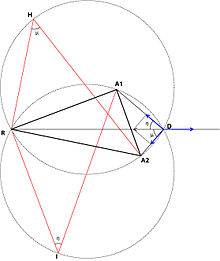
Для задачі притягання-відштовхування в разі трикутника існує геометричне розв'язання, відкрите відносно недавно[7]. Воно відрізняється від двох попередніх, оскільки в цьому випадку трикутники сил, що будуються, накладаються на трикутник розміщення точок A1A2R (тут A1 і A2 — точки притягання, а R — точка відштовхування).
Розв'язання таке:
1. У трикутнику RA2H, що будується, який накладається частково на трикутник розміщення точок A1A2R, сторона RA2 пропорційна силі притягання A1w у напрямку до A1, сторона RH пропорційна силі притягання A2w у напрямку до A2, а сторона A2H пропорційна силі відштовхування Rw у напрямку R.
2. У трикутнику RA1I, що будується, який накладається частково на трикутник розміщення точок A1A2R, сторона RA1 пропорційна силі притягання A2w у напрямку до A2, сторона RI пропорційна силі притягання A1w у напрямку до A1, а сторона A1I пропорційна силі відштовхування Rw у напрямку від R;
3. Оптимальна точка D розташовується на перетині двох описаних навколо побудованих трикутників RA2H і RA1I кіл. Розв'язання не виходить, якщо одна зі сил більша за суму двох інших або якщо кути не порівнянні. У деяких випадках цих порушень немає (ніяка сила не більша за суму двох інших і кути порівнянні), але оптимальний розв'язок збігається з точкою з більшою силою тяжіння.
Тригонометричне розв'язання Тельє задач Ферма та Вебера[ред. | ред. код]

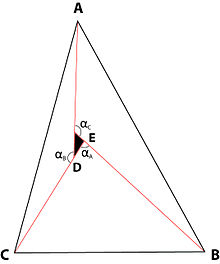
Понад 332 роки відокремлюють формулювання задачі Ферма для трикутника та відкриття неітеративного чисельного розв'язання, хоча геометричне розв'язання існувало майже весь цей період. Пояснюється це тим, що початки трьох векторів, спрямованих до трьох точок тяжіння, можуть не збігатися. Якщо вони збігаються і лежать в оптимальній точці P, вектори в напрямку до A, B і C і сторони трикутника точок притягання ABC утворюють шість кутів ∠1, ∠2, ∠3, ∠4, ∠5 і ∠6, а три вектори утворюють кути ∠αA, ∠αB та ∠αC. Легко записати такі шість рівностей, що пов'язують шість невідомих (кути ∠1, ∠2, ∠3, ∠4, ∠5 і ∠6) із шістьма відомими значеннями (кути ∠A, ∠B і ∠C задані, а значення кутів ∠αA, ∠αB і ∠αC залежить тільки від відносних значень трьох сил притягання до точок A, B і C):
- ∠1 + ∠2 = ∠C ;
- ∠3 + ∠4 = ∠A ;
- ∠5 + ∠6 = ∠B ;
- ∠1 + ∠6 + ∠αA = 180° ;
- ∠2 + ∠3 + ∠αB = 180° ;
- ∠4 + ∠5 + ∠αC = 180°.
На жаль, ця система шести рівнянь є невизначеною і можливість того, що початки трьох векторів у напрямку точок притягання не збігаються, пояснює чому. У разі розходження легко бачити, що рівняння залишаються правильними. Однак оптимальне положення точки P зникає через трикутну «дірку» всередині трикутника. Фактично, як показав Тельє (1972)[2], ця трикутна діра має такі ж пропорції, що й «трикутники сил», які ми будували в геометричному розв'язанні Сімпсона.
Щоб розв'язати задачу, слід додати до вказаних шести рівнянь сьоме, яке має запобігти появі трикутної «дірки» в центрі трикутника точок притягання. Іншими словами, початки векторів повинні збігатися.
Розв'язання Тельє задач Ферма та Вебера для трикутника здійснюється за три кроки:
1. Визначаємо кути ∠αA, ∠αB та ∠αC, за яких три сили притягання Aw, Bw та Cw компенсують одна одну, забезпечуючи рівновагу. Для цього використовуємо такі рівняння:
- cos ∠αA = −(Bw2 + Cw2 − Aw2) / (2 Bw Cw) ;
- cos ∠αB = −(Aw2 + Cw2 − Bw2) / (2 Aw Cw) ;
- cos ∠αC = −(Aw2 + Bw2 − Cw2) / (2 Aw Bw) ;
2. Визначаємо величину кута ∠3 (ця рівність забезпечує збіг точок D та E):
- tan ∠3 = (k sin k') / (1 + k cos k') ;
де k = (CB/CA) (sin ∠αB / sin ∠αA), а k' = (∠A +∠B + ∠αC) − 180° ;
3. Розв'язуємо систему рівнянь, у якій ∠3 вже відомий:
- ∠1 + ∠2 = ∠C ;
- ∠3 + ∠4 = ∠A ;
- ∠5 + ∠6 = ∠B ;
- ∠1 + ∠6 + ∠αA = 180° ;
- ∠2 + ∠3 + ∠αB = 180° ;
- ∠4 + ∠5 + ∠αC = 180°.
Тригонометричне розв'язання Тельє задачі притягання-відштовхування[ред. | ред. код]
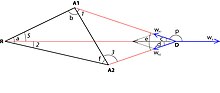

Тельє (1985)[6] розширив задачу Ферма — Вебера для сил відштовхування. Розглянемо випадок для трикутника, в якому діють дві сили притягання A1w та A2w та одна сила відштовхування Rw. Тут, як і в попередньому випадку, можливий випадок розходження початків трьох векторів. Таким чином, розв'язання має вимагати їхнього збігу. Тригонометричне розв'язання Тельє цієї задачі таке:
1. Визначаємо кут ∠e:
- cos ∠e = −(A1w2 + A2w2 − Rw2) / (2 A1w A2w) ;
2. Визначаємо кут ∠p:
- cos ∠p = −(A1w2 + Rw2 − A2w2) / (2 A1w Rw) ;
3. Визначаємо кут ∠c:
- ∠c = 180° − ∠p ;
4. Визначаємо кут ∠d:
- ∠d = ∠e − ∠c ;
5. Визначаємо значення кута ∠3 (це рівняння вимагає збігу точок D та E):
- tan ∠3 = x/y ;
де x = sin ∠f — (RA1/RA2)(sin ∠d sin [∠e − ∠b] / sin ∠c) ; і y = (RA1/RA2)(sin ∠d cos [∠e − ∠b] / sin ∠c) − cos ∠f ;
6. Визначаємо кут ∠1:
- ∠1 = 180° − ∠e − ∠3 ;
7. Визначаємо кут ∠5:
- ∠5 = 180° − ∠b − ∠c − ∠1 ;
8. Визначаємо кут ∠2:
- ∠2 = ∠a − ∠5.
Ітеративне розв'язання задач Ферма, Вебера та притягання-відштовхування[ред. | ред. код]
Якщо число сил більше трьох, неможливо визначити кути без розгляду геометрії многокутника точок притягання. Геометричні та тригонометричні методи безсилі. У таких випадках використовують ітеративні оптимізаційні методи. Кун і Куен (1962)[1] запропонували алгоритм, заснований на ітераційному зваженому методі найменших квадратів[en], що узагальнює алгоритм Вайсфельда для незваженої задачі. Їхній метод працює для задач Ферма та Вебера, в яких є багато сил, але не для задач притягання-відштовхування. У цьому методі для знаходження наближення до точки y, яка мінімізує зважену суму відстаней
береться початковий розв'язок y0 і на кожному кроці алгоритм наближається до оптимального розв'язку вибором yj+1, яке мінімізує зважену суму відстаней
- ,
де початкові ваги wi діляться на відстань від точки до наближення попереднього кроку. Кожне наступне наближення можна отримати як зважене середнє єдиного оптимального розв'язку зваженого методу найменших квадратів:
Для задачі притягання-відштовхування можна скористатися алгоритмом, який запропонували Чен, Гансен, Жомар і Туй (1992)[8].
Інтерпретація теорії вартості землі у світлі задачі тяжіння-відштовхування[ред. | ред. код]
У світі економічної теорії використання простору сили відштовхування всюдисущі. Гарним прикладом є вартість землі. Значну частину теорії вартості землі, як сільської, так і міської, можна підсумувати так.
У випадку, коли всіх приваблює єдина точка тяжіння (сільський ринок або центральний діловий район міста), змагання різних учасників торгів, які бажають розміститися в центрі, утворює ціну землі, яка перетворює точку притягання системи на точку відштовхування, що визначається високою вартістю землі, і кожен житель і ділова активність розміщується в точці, де сили притягання та відштовхування компенсуються.
Задача притягання-відштовхування та нова економічна географія[ред. | ред. код]
Оттавіно і Тісс (2005)[9] розглядають задачу Тельє як прелюдію «нової економічної географії» (НЕГ), розробленої в 1990-х роках, за яку Пол Круґман 2008 року отримав Нобелівську премію з економіки. Концепція сил притягання споріднена з концепцією агломерації або відцентрових сил НЕГ, а концепція сил відштовхування споріднена з концепцією розосередження або відцентрових сил.
Примітки[ред. | ред. код]
- ↑ а б Kuhn, Kuenne, 1962, с. 21–34.
- ↑ а б Tellier, 1972, с. 215–233.
- ↑ Simpson, 1750.
- ↑ Weber, 1922.
- ↑ Тут йдеться про сили, не аналогічні гравітаційним чи електричним, оскільки ці сили не залежать від відстані.
- ↑ а б Tellier, 1985.
- ↑ Tellier, 2013.
- ↑ Chen, Hansen, Jaumard, Tuy, 1992, с. 467–486.
- ↑ Ottaviano, Thisse, 2005, с. 1707–1725.
Література[ред. | ред. код]
- Pey-Chun Chen, Pierre Hansen, Brigitte Jaumard, Hoang Tuy. Weber's Problem with Attraction and Repulsion // Journal of Regional Science. — 1992. — Вип. 32.
- Harold W. Kuhn, Robert E. Kuenne. An Efficient Algorithm for the Numerical Solution of the Generalized Weber Problem in Spatial Economics // Journal of Regional Science. — 1962. — Вип. 4.
- Gianmarco Ottaviano, Jacques-François Thisse. New Economic Geography: what about the N? // Environment and Planning A. — 2005. — Вип. 37.
- Thomas Simpson. The Doctrine and Application of Fluxions. — London, 1750.
- Luc-Normand Tellier, Boris Polanski. The Weber Problem: Frequency of Different Solution Types and Extension to Repulsive Forces and Dynamic Processes // Journal of Regional Science. — 1989. — Т. 29, вип. 3. — С. 387–405.
- Luc-Normand Tellier. The Weber Problem: Solution and Interpretation // Geographical Analysis. — 1972. — Т. 4, вип. 3.
- Luc-Normand Tellier. Économie spatiale: rationalité économique de l'espace habité. — Chicoutimi : Gaëtan Morin éditeur, 1985.
- Luc-Normand Tellier. Sciences du territoire II : methodologies / Marc-Urbain Proulx. — Québec : Presses de l’Université du Québec, 2013.
- Alfred Weber. Über den Standort der Industrien. — Tübingen : J.C.B. Mohr, 1922.
- Alfred Weber. The Theory of the Location of Industries. — Chicago : Chicago University Press, 1929. — переклад англійською
- Georges Wesolowski. The Weber problem: History and perspective // Location Science. — 1993. — Т. 1. — С. 5–23.
Посилання[ред. | ред. код]
- Hazewinkel, Michiel, ред. (2001), Задача Вебера, Математична енциклопедія, Springer, ISBN 978-1-55608-010-4


