Süperakışkan helyum-4

Vikipedi, özgür ansiklopedi

Süperakışkan Helyum-4, helyum elementi helyum-4 ün oluşturduğu bir süper akışkandır. Bir süperakışkan maddenin 0 viskoziteli bir akışkan gibi davrandığı durumudur. Normal bir sıvı gibi görünen madde her tür yüzeyde sürtünmesiz şekilde engellerin etrafından dolaşır ve kabının gözeneklerinden yalnızca kendi eylemsizliğine bağlı olarak akar.

Kuantum hidrodinamiği ve makroskopik kuantum fenomeninin önemli kısmı olarak bilinen süperakışkanlık Pyotr Kapitsa,[1] John F. Allen ve Don Misener[2] tarafından 1937’de keşfedilmiştir. Olgusal ve mikroskobik teorilerle tanımlanagelmiştir. Süperakışkanın formasyonu Bose-Einstein yoğuşmasının formasyonuyla ilgili olarak bilinir. Bu sıvı helyum-4 te helyum-3 e göre çok daha yüksek sıcaklıklarda süperakışkanlık oluşacağı durumunu bariz kılar. Helyum-4 ün her atomu sıfır dönmesinin etkisiyle bir bozon parçacığıdır. Helyum-3 ise bozonları çok daha alçak sıcaklıklarda süperiletkenlikteki elektron gruplamasına benzer şekilde yalnızca kendisiyle gruplayarak oluşturan bir fermiyon parçacığıdır.

1950’lerde, Hall ve Vinen süperakışkan helyumda nicel girdap doğrılarının varlığını belirleyen deneyler yaptılar.[3] 1960’larda Rayfield ve Reif nicel girdap halkalarının varlığını kanıtladı.[4] Packard girdap doğruları ile akışkanın[5] serbest yüzeyinin kesişimini gözlemledi ve Avenel ve Varoquaux süperakışkan helyum-4[6] te Josephson efekti üzerinde çalıştılar.[7]

Özellikler[değiştir | kaynağı değiştir]

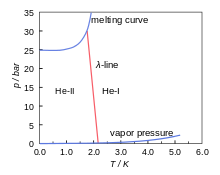
Fig.1. 4He faz diyagramı. Bu diyagramda λ doğrusu ayrıca verilmiştir.
Fig.3. Normal ve süperakışkan bileşenlerin (ρn/ρ ve ρs/ρ) sıcaklığa bağlı değişimi .

Figür 4He nin faz diagramıdır.[8] Bu erime eğrisi (sıvı ve katı durum arasında) tarafından ayrılan katı ve sıvı bölgeleri ; buhar basıncı doğrusuyla ayrılan gaz ve sıvı bölgeleri gösteren bir p-T (basınç-sıcaklık) grafiğidir. İkincisi gaz ve sıvı arasındaki farkın yok olduğu kritik noktada biter. Bu diyagram  4He'nin dikkat çekici şekilde mutlak 0’ da dahi sıvı olma özelliğini gösterir. Helyum-4 yalnızca 25 barın üstündeki basınçlarda katıdır.

Figür 1 ayrıca λ doğrusunu da gösterir. Bu doğru He-I ve He-II tarafından belirtilen faz diyagramındaki iki sıvı bölgeyi ayıran doğrudur. He-I bölgesinde helyum normal bir sıvı gibi davranır ; He-II de ise helyum süperakışkandır.

Lambda- doğrusu ismi spesifik bir sıcaklıktan gelir—Yunan harfi λ şeklinde olan bir sıcaklık grafiği.[9][10] 2.172 K’ de bir zirve (4He nin sözde λ zirvesi) gösteren Figür 2’ye bakınız .

Lambda doğrusunun altında sıvı sözde iki-akışkan modeli ile tanımlanabilir. Sanki iki bileşenden oluşuyormuş gibi davranır: normal bir akışkan gibi davranan bir normal bileşeni ve sıfır viskoziteli ve entropili bir süperakışkan bileşeni. Yoğunlukların oranları ρn/ρ ve ρs/ρ, ile normal(süperakışkan) bileşenin yoğunluğu ρn (ρs) ve toplam yoğunluk ρ sıcaklığa bağlıdır ve Figür 3’te gösterilmiştir.[11] Sıcaklığı azaltarak süperakışkan yoğunluğun kesri  Tλ da sıfırdan, 0 Kelvinde 1 e yükselir. 1 K altında helyum neredeyse tamamen süperakışkandır.

Normal bileşenin (aynı zamanda ρn + ρs ρs = sabit olduğundan süperakışkan bileşenin) basit ses dalgalarına benzer yoğunluk dalgalarını oluşturmak mümkündür. Bu etki ikinci ses olarak adlandırılır. ρn in sıcaklığa olan bağımlılığı nedeniyle (figür 3 ) ρn içindeki bu dalgalar ayrıca sıcaklık dalgalarıdır.

Fig.4. Helyum II kendi seviyesini bulmak için yüzeyler boyunca kayar-kısa bir süre sonra iki kapta da su seviyeleri eşitlenir. Rollin filmi büyük kabın içini korur, eğer mühürlü değilse Helyum II dışarıya kaçabilir.
Fig.5. Süperakışkan fazındaki sıvı helyum. Süperakışkan olarak kaldıkça ince bir film gibi kabın duvarlarında yukarı sürünür. Kenarlardan aşağıya gelerek aşağıdaki sıvıya düşmek üzere damlalar oluşturur. Bu olay kap boşalana kadar devam eder.

Film akışı[değiştir | kaynağı değiştir]

Alkol ve petrol gibi birçok sıradan sıvı yüzey gerilimlerinden dolayı katı duvarlara sürünerek ilerler. Sıvı helyum da bu özelliğe sahiptir, fakat H-II nin durumunda, sıvının yüeyde akışı viskozitesi tarafından kısıtlanmamıştır ancak yaklaşık 20 cm/s lik bir kritik hız tarafından kısıtlanmıştır. Bu süperakışkan bir figür 4’te gösterildiği gibi sifon efekti içerisinde helyumun kapların duvarlarında nispeten kolay tırmanabilmesi ve aynı şekilde sıvının yüzeyine inmesi için oldukça yüksek bir hızdır. Bir kapta sıvı seviyesi yukarı kaldırılırsa figür 5 ‘ teki gibi görülebilen damlacıklar oluşturur.

Süperakışkan Hidrodinamiği[değiştir | kaynağı değiştir]

Süperakışkan bileşeninin hareketi için eşitlik (bir miktar basitleştirilmiş halde)[12] Newton yasaları tarafından verilmiştir:

M4 ağırlığı  4He nin molar ağırlığı ve   de süperakışkan bileşenin hızıdır. Zaman türevi sözde hidrodinamik türevdir, diğer bir deyişle akışkanla hareket ederken hızın artışıdır. Süperakışkan 4He nin durumunda yerçekimsel alan şu şekilde verilmiştir:[13][14] . Bu gösterimde μ molar kimyasal potansiyel, g yerçekimsel ivme ve z dikey koordinattır. Böylece:

   

 

 

 

 

(1)

   

Eşitlik(1) yalnızca vs akış kanalının çapı tarafından belirlenen kritik bir değerin altında ise tutar.[15][16]

Klasik mekanikte güç genellikle bir potansiyel enerjinin düşümüdür. Eşitlik(1) gösterir ki süperakışkan bileşeninin durumunda kuvvet, kimyasal potansiyelin bir düşümüne bağlı bir terim içerir.

Fıskiye Basıncı[değiştir | kaynağı değiştir]

Eşitlik(1) i daha tanıdık bir şekilde yeniden yazılımı için aşağıdaki formülü kullanırız:

   

 

 

 

 

(2)

   

Burada Sm molar entropi ve Vm molar hacimdir. Eşitlik(2) ile µ(p,T) p-T düzleminin integraliyle bulunabilir. İlk olarak orijin (0,0) den (p,0) a kadar integral alırız böylece T=0 olur. Sonra (p,0) dan (p, T) ye yani sabit basınçla integral alırız (figür 6’ya bakınız). İlk integralde dT=0 ve ikincide dp=0 dır. Eşitlik(2) ile şunu elde ederiz:

   

 

 

 

 

(3)

   

Yalnızca p nin küçük olup  Vm nin pratikte sabit olduğu durumla ilgileniriz. Böylece :

   

 

 

 

 

(4)

   

Vm0 sıvının T=0 ve p=0 daki molar hacmidir. Eşitlik(3) teki diğer terimVm0 ve bir basınç ölçüsüne sahip pf değerinin bir ürünü olarak yazılabilir.

   

 

 

 

 

(5)

   

pf basıncı fıskiye basıncı olarak adlandırılır. Bu basınç ısı kapasitesinden sırayla hesaplanabilen 4He nin entropisinden hesaplanabilir. T =Tλ için fıskiye basıncı 0.692 bara eşittir.125 kg/m3 yoğunlukta g = 9.8 m/s2 de 56 metre yükseklikte bir sıvı helyum sütununa karşılık gelir. Yani, birçok deneyde, süperakışkan helyumun hareketinde, fıskiye basıncının yerçekiminden daha büyük bir etkisi vardır.

Eşitlik(4) ve Eşitlik (5) ile Eşitlik(3) bu hali alır:

   

 

 

 

 

(6)

   

Eşitlik(6), ve Eşitlik(1) in yerlerine konmasıyla:

   

 

 

 

 

(7)

   

ρ₀ = M4/Vm0 ile sıfır basınç ve sıcaklıkta sıvı 4He nin yoğunluğu.

Eşitlik(7) süperakışkan bileşenin basınç ve yerçekimsel alandaki düşümler tarafından hızlandırıldığını gösterir; ayrıca fıskiye basıncının düşümünden de etkilenir.

Buraya kadar Eşitlik(5) yalnızca matematiksel bir anlama sahiptir, ancak özel deneylsel düzenlemelerde pf gerçek bir basınç gibi ortaya çıkabilir. Figür 7 He-II içeren iki kap gösterir. Soldaki kabın 0 Kelvin(Tl=0) ve 0 basınçta  (pl = 0).olduğu kabul edilir. Kaplar bir sözde sızıntı borusu ile bağlanmıştır. Bu çok ince tozla doldurulmuş bir tüptür yani normal bileşenin hareketi engellenmiştir. Ancak süperakışkan bileşken bir sorun olmadan ilerleyebilir (yaklaşık 20 cm/s lik kritik hızın altında bir hızla). Sabit durumda vs=0 yani Eşitlik(7) şunu gösterir :

   

 

 

 

 

(8)

   

İndis I (r) sızıntı borusunun sol (sağ) tarafında doğru uygulanır. Bu özel durumda  pl = 0, zl = zr, ve pfl = 0 (Tl = 0 olduğundan). Sonuç olarak,

Bu Tr da sağ kaptaki basıncın fıskiye basıncına eşit olduğu anlamına gelir.

Figür 8’deki gibi düzenlenmiş bir deneyde bir fıskiye oluşturulabilir. Fıskiye efekti seyrelti soğutucularında 3He sirkülasyonunu yönlendirmek için kullanılır.[17][18]

Isı Nakli[değiştir | kaynağı değiştir]

Figür 9 He-II ile dolu bir tüp tarafından bağlanmış iki TH and TL arasında ısı iletim deneyini tasvir eder. Sıcaklık sıcak uca uygulandığında Eşitlik(7) ye göre sıcak uçta bir basınç gelişir. Bu basınç normal bileşeni sıcak uçtan soğuk uca şu eşitliğe göre götürür:

Burada ηn normal bileşenin viskozitesi,[19] Z bir geometrik faktör ve   debi hacmidir. Normal debi soğuk uçtan sıcak uca süperakışkan bileşenin debisi tarafından dengelenmiştir. Uç kısımlarda normal bileşenle süperakışkan bileşen arasında dönüşümler meydana gelir. Böylece ısı iletim yoluyla değil de konveksiyon yoluyla taşınmış olur. Bu tarz ısı iletimi çok etkilidir yani He-II nin termal iletimi en iyi maddelerden çok daha iyidir. Bu durum ısının gaz-sıvı dönüşümüyle taşındığı ısıtma borularıyla karşılaştırılabilir. He-II nin yüksek termal iletkenliği CERN’deki Büyük Hadron Çarpıştırıcısı’ndaki süperiletken mıknatısların stabilize edilmesi için kullanılmaktadır.

Teori[değiştir | kaynağı değiştir]

Landau iki-akışkan yaklaşımı[değiştir | kaynağı değiştir]

L. D. Landaunun fenomenolojik ve yarı mikroskopik helyum-4 süperakışkanlık teorisi 1962’de kendisine Nobel Fizik Ödülünü kazandırmıştır. Düşük sıcaklıklarda ses dalgalarının helyum-4 için en önemli uyarıcı olduğunu varsayarak, eğer akış hızı ses hızından düşükse bir duvarda akan helyum-4 ün spontane uyarılar oluşturmayacağını göstermiştir. Bu modelde ses hızı, geçildiği takdirde süperakışkanlığın yok olduğu kritik hızdır. ( Aslında Helyum-4 ses hızından daha düşük bir akış hızına sahiptir, ancak bu model konsepti göstermek için kullanışlıdır.). Landau ayrıca yoğuşma olarak da bilinen ses dalgası ve diğer uyarıcıların birbirleriyle dengelenip kalan helyum-4 ten ayrı yönlere akabileceğini de göstermiştir.

Uyarıların momentum ve akış hızından yola çıkarak 0 sıcaklıkta 0 olan ve sıcaklıkla birlikte artan bir ” normal akışkan “ yoğunluğu tanımlayabilmiştir. Normal akışkan yoğunluğunun toplam yoğunluğa eşit olduğu sözde Lambda sıcaklığında helyum-4 artık süperakışkan değildir.

Landau süperakışkan helyum-4 üzerinde erken spesifik ısı verisini açıklamak için kendisinin “roton” diye adlandırdığı bir takım uyarıların olduğunu varsaymıştır, ancak veriler ulaşılabilir oldukça “roton” un sesin yüksek momentum versiyonuyla aynı olduğunu görmüştür.

Landau teorisi sıvı helyumun süperakışkan bileşiğinin mikroskobik yapısı üzerinde ayrıntılı şekilde durmaz. Süperakışkan bileşenin mikroskobik teorisini oluşturmak için ilk denemeyi London[20] ve Tisza[21][22] yapmış, sonradan farklı kişiler tarafından başka mikroskobik modeller önerilmiştir. Ana gayeleri kuantum mekaniğinin ilk prensibinden yola çıkarak süperakışkan halindeki helyum atomları arasındaki parçacıklar arası potansiyeli türetmekti. Bugüne kadar bu tarz birkaç model önerilmiştir: girdap halkalı modeller, sert küre modelleri, Gauss küme teorileri vs.

Girdap Halkası Modeli[değiştir | kaynağı değiştir]

Landau girdap etkisinin süperakışkan helyum-4 e girdap tabakalarından girdiğini düşündü, ancak böyle tabakalar kararsız olarak görünmekteydi. Lars Onsager ve (daha sonra bağımsız olarak) Feynman girdap etkisi nicelenmiş girdap doğruları aracılığıyla girer. Ayrıca kuantum girdap halkaları fikrini de geliştirmişlerdir. 1940 ‘larda[23] Arie Bijl ve 1955[24] civarında Richard Feynman, roton için Palevsky tarafından inelastik nötron deneyleriyle kısaca gözlemlenen mikroskobik teoriler geliştirdiler. Daha sonra Feynman kendi modelinin deneyle yalnızca nitel uyuşma sağladığını itiraf etmiştir.[25][26]

Sert Küre modelleri[değiştir | kaynağı değiştir]

Bu modeller süperakışkan fazındaki helyum-4 atomları arasındaki parçacık arası potansiyelin sadeleştirilmiş formuna dayanır. Yani potansiyelin sert-küre tarzında olduğu varsayılır.[27][28][29] Bu modellerde uyarıların ünlü Landau (roton) spektrumu nitel olarak yeniden üretilmiştir.

Gauss küme yaklaşımı[değiştir | kaynağı değiştir]

Bu helyum-4 ün süperakışkan bileşenini tanımlayan 2 ölçekli bir yaklaşımdır. Parametrik alanla bağlı iç içe geçmiş iki modelden oluşur. Kısa dalgaboylu kısım Logaritmik Schrödinger eşitliğine dayanan sarsılmaz bir yaklaşım kullanarak akışkan birimin iç tarafını tanımlar; iç yoğunluğun ve parçacık arası etkileşim potansiyelinin Gauss tarzı davrandığını öne sürer. Uzun dalgaboylu kısım bu birimlerin dinamik ve etkileşimleriyle uğraşan kuantum çoklu cisim teorisidir. Bu yaklaşım fonon, maxon ve roton uyarılmalarının birleşik bir tanımını sağlar ve deneyle dikkatedeğer bir uyuşması vardır: Temel bir parametre ile süperakışkan helyum-4 ün Landau roton spektrumu, ses hızı ve yapı faktörünü yüksek doğrulukla yeniden üreten biriyle uyuşturmak.[30] Bu model quantum Everett-Hirschmanentropi fonksiyonuyla ilgili olan enerjiye harcama-tarzı katkıyı ortaya koymaya dayanan kuantum Bose sıvıları ile logaritmik doğrusal olmama[31] genel teorisini kullanır.[32][33]

Arka plan[değiştir | kaynağı değiştir]

Süperakışkan durumundaki helyum-4 ve helyum-3 hakkındaki fenomenolojiler çok benzer olsa da geçişlerin mikroskobik detayları çok farklıdır. Helyum-4 atomları bozonlardır ve süperakışkanlıkları uydukları Bose-Einstein istatistikleri açısından anlaşılabilir. Spesifik olarak helyum-4 ün süperakışkanlığı etkileşen bir sistemde Bose-Enstein yoğuşmasının bir sonucu olarak görülebilir. Diğer yandan helyum-3 atomları fermiyonlardır ve bu sistemdeki süperakışkan geçişi süperiletkenliğin BCS teorisinin bir genellemesi tarafından tanımlanır. Bunun içerisinde elektronlar yerine atomlar arasında Cooper gruplaması yer alır ve onlar arasındaki çekim gücü fononlar yerine dönüş dalgalanmaları tarafından ortaya çıkar. (Fermiyon yoğuşmasına bakınız.) Süperiletkenlik ve süperakışkanlığın birleşik bir tanımı gösterge simetri kırılması açısından mümkündür.

Lambda noktasının altındaki helyum-4 gibi süperakışkanlar birçok tuhaf özellik sergilerler. Bir süperakışkan sanki normal bir sıvının tüm özelliklerine sahip bir normal bileşen ve bir süperakışkan bileşenin karışımı gibi davranır. Süperakışkan bileşenin entropisi ve viskozitesi sıfırdır. Süperakışkan helyumda bir yere ısı uygulanması çok yüksek etkili termal iletim sağlayan nispeten yüksek bir hızda (20 cm/s ye kadar) ısı nakliyle ilgilenen normal bileşenin akışına yol açar.

Süperakışkan dönen bir kaba konulursa diğer bir önemli özellik ortaya çıkar. Kapla aynı şekilde dönmek yerine, dönmekte olan durum nicel girdaplardan meydana gelir. Bu kap ilk kritik açısal hız altında bir hızda dönerken sıvının tamamen sabit kaldığı anlamına gelir. İlk krtik açısal hıza ulaşıldığı anda süperakışkan bir girdap oluşturur. Girdap gücü niceldir, bu da bir süperakışkanın yalnızca belirli “izin verilmiş” değerlerde dönebileceği demektir. Su gibi normal bir akışkandaki dönme nicel değildir. Dönme hızı arttıkça bir süperiletkendeki Abrikosov kafesine benzer şekilde güzel modellerde düzenlenmiş nicel girdaplar oluşacaktır.

Pratik Uygulama[değiştir | kaynağı değiştir]

Son zamanlarda kimya alanında, süperakışkan helyum-4 bir kuantum çözücü olarak spektroskopik tekniklerde başarıyla kullanılmaktadır. Süperakışkan helyum damlacık spektroskopisinde ifade edildiği gibi süperakışkan ortamda çözünmüş tek bir molekül bir molekülün etkin bir dönme özgürlüğüne sahip olmasına yani gaz halindeymiş gibi davranmasına izin verir. Süperakışkan helyum damlacıkları ayrıca çözünen molekülleri temel hallerine ya da yakınlarına kadar soğutan yaklaşık 0.4 K lik karakteristik bir sıcaklığa sahiptir.

Süperakışkanlar ayrıca teorik olarak tahmin edilen yerçekimsel etkilerin ölçümüne olanak sağlayan jiroskop gibi yüksek hassasiyetli cihazlarda da kullanılır. (Gravity Probe B ye bakınız.)

1999’da bir çeşit süperakışkan ışığı tuzağa düşürmek ve hızını büyük ölçüdde azaltmak için kullanılmıştır. Lene Hau tarafından yapılan bir deneyde ışık bir Bose-Einstein yoğuşmalı sodyum gazından geçirilmiş(bir süperakışkana benzer şekilde) ve boşluktaki normal hızı 299,792,458 m/s lik normal hızından 17 m/s (61 km/h) ye kadar yavaşladığı görülmüştür.[34] Bu c nin mutlak değerini değiştirmez ya da tamamen yeni bir şey değildir: boşluk dışında her ortam (su veya cam gibi) ışığın yayılmasını n maddenin kırınım indisi olmak üzere c/n’ e yavaşlatır. Işığın çok yavaş hızı ve yüksek kırılma indisi bu özel deneyde gözlemlemiştir, diğer taraftan bu tüm süperakışkanlar için genel bir özellik değildir.

Kızılötesi Astronomik Uydu IRAS Ocak 1983’te 73 kg süperakışkan helyum tarafından 1.6 K  (−271.55 °C) lik sıcaklık korunarak soğutulan kızılötesi veriyi toplamak için fırlatılmıştır. Ayrıca Helyum-3 ile birleşik halde kullanıldığında, aşırı düşük sıcaklık deneylerinde 40 mK e kadar düşük sıcaklıklara ulaşılmıştır. 3.2 K de sıvı haldeki Helyum-3 bir gaz olarak davrandığı süperakışkan helyum-4 e buharlaştırılabilir. Bu buharlaştırma bütün sistemden normal soğutma teknikleriyle tamamen aynı şekilde dışarıya pompalanabilen bir enerji çeker.

Süperakışkan helyum teknolojisi kryojeniklerin sıcaklık menzilini daha düşük sıcaklıklara yaymak için kullanılmaktadır. Şimdiye kadar limit 1.19 K dir, ancak 0.7 K’ye ulaşma potansiyeli vardır.[35]

21. yüzyıl gelişmeleri[değiştir | kaynağı değiştir]

2000’lerin başlarında fizikçiler ultra soğuk fermiyonik atom gruplarından Fermiyonik yoğuşma oluşturdular. Belirli şartlar altında fermiyon grıpları diatomik moleküller oluşturur ve Bose-Einstein yoğuşmasına uğrar. Diğer tarafta fermiyonlar(özellikle süperiletken elektronlar) süper akışkanlık gösteren Cooper grupları oluşturur. Ultra-soğuk atomik gazlarla yapılan bu çalışma bilimadamlarına BEC-BCS geçiti olarak bilinen bu iki uç arasında çalışma imkânı vermiştir.

Süper katılar da Penn State Üniversitesindeki fizilçiler tarafından 2004’te keşfedilmiş olabilir. Helyum-4 yüksek basınçlar altında yaklaşık 200 mK nin altına kadar soğutulduğunda, katının bir kısmı (~%1) süperkatı olarak görünür.[36][37] Söndürme soğutma teknikleri veya tavlama zamanının aydınlatılmasıyla kusur yoğunluğunun nispeten artıp veya azalmasıyla, burulmayla ilgili osilatör deneyiyle süperkatı kesri tamamen varolmayandan %20’lik bir menzile çıkarılabilir. Bu helyum-4 ün süperkatı doğasının gerçek olmadığını ancak helyum-4 ün bir özelliği ve düzensizliği olduğunu öne sürer.[38][39] Gelişmekte olan bazı teoriler helyum-4 te gözlemlenen süperkatı sinyallerinin bir süpercam durumu ya da aslen helyum-4 kristalleri[40] içinde süperakışkan tanecik sınırları olduğunu varsayar.[41]

Kaynakça[değiştir | kaynağı değiştir]

  1. ^ Kapitza, P. (1938). "Viscosity of Liquid Helium Below the λ-Point". Nature. 141 (3558). s. 74. Bibcode:1938Natur.141...74K. doi:10.1038/141074a0. 
  2. ^ Allen, J. F.; Misener, A. D. (1938). "Flow of Liquid Helium II". Nature. 142 (3597). s. 643. Bibcode:1938Natur.142..643A. doi:10.1038/142643a0. 
  3. ^ Hall, H. E.; Vinen, W. F. (1956). "The Rotation of Liquid Helium II. II. The Theory of Mutual Friction in Uniformly Rotating Helium II". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 238 (1213). s. 215. Bibcode:1956RSPSA.238..215H. doi:10.1098/rspa.1956.0215. 
  4. ^ Rayfield, G.; Reif, F. (1964). "Quantized Vortex Rings in Superfluid Helium". Physical Review. 136 (5A). ss. A1194. Bibcode:1964PhRv..136.1194R. doi:10.1103/PhysRev.136.A1194. 
  5. ^ Packard, Richard E. (1982). "Vortex photography in liquid helium". Physica B+C. Cilt 109–110. s. 1474. Bibcode:1982PhyBC.109.1474P. doi:10.1016/0378-4363(82)90510-1. 
  6. ^ Avenel, O.; Varoquaux, E. (1985). "Observation of Singly Quantized Dissipation Events Obeying the Josephson Frequency Relation in the Critical Flow of Superfluid ^{4}He through an Aperture" (PDF). Physical Review Letters. 55 (24). ss. 2704-2707. Bibcode:1985PhRvL..55.2704A. doi:10.1103/PhysRevLett.55.2704. PMID 10032216. 
  7. ^ Bewley, Gregory P.; Lathrop, Daniel P.; Sreenivasan, Katepalli R. (2006). "Superfluid helium: Visualization of quantized vortices" (PDF). Nature. 441 (7093). s. 588. Bibcode:2006Natur.441..588B. doi:10.1038/441588a. PMID 16738652. 3 Ağustos 2016 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 26 Mayıs 2016. 
  8. ^ Swenson, C. (1950). "The Liquid-Solid Transformation in Helium near Absolute Zero". Physical Review. 79 (4). s. 626. Bibcode:1950PhRv...79..626S. doi:10.1103/PhysRev.79.626. 
  9. ^ Keesom, W.H.; Keesom, A.P. (1935). "New measurements on the specific heat of liquid helium". Physica. Cilt 2. s. 557. Bibcode:1935Phy.....2..557K. doi:10.1016/S0031-8914(35)90128-8. 
  10. ^ Buckingham, M.J.; Fairbank, W.M. (1961). Chapter III The Nature of the λ-Transition in Liquid Helium"The nature of the λ-transition in liquid helium". Progress in Low Temperature Physics. Cilt 3. s. 80. doi:10.1016/S0079-6417(08)60134-1. ISBN 9780444533098. 
  11. ^ E.L. Andronikashvili Zh. Éksp.
  12. ^ S.J. Putterman, Superfluid Hydrodynamics (North-Holland Publishing Company, Amsterdam, 1974) ISBN 0444106812
  13. ^ L.D. Landau, J. Phys.
  14. ^ I.M. Khalatnikov, An introduction to the theory of superfluidity (W.A. Benjamin, Inc., New York, 1965) ISBN 0738203009.
  15. ^ Van Alphen, W.M.; Van Haasteren, G.J.; De Bruyn Ouboter, R.; Taconis, K.W. (1966). "The dependence of the critical velocity of the superfluid on channel diameter and film thickness". Physics Letters. 20 (5). s. 474. Bibcode:1966PhL....20..474V. doi:10.1016/0031-9163(66)90958-9. 
  16. ^ De Waele, A.Th.A.M.; Kuerten, J.G.M. (1992). Chapter 3: Thermodynamics and Hydrodynamics of 3He-4He Mixtures"Thermodynamics and hydrodynamics of 3He-4He mixtures". Progress in Low Temperature Physics. Cilt 13. s. 167. doi:10.1016/S0079-6417(08)60052-9. ISBN 9780444891099. 
  17. ^ Staas, F.A.; Severijns, A.P.; Van Der Waerden, H.C.M. (1975). "A dilution refrigerator with superfluid injection". Physics Letters A. 53 (4). s. 327. Bibcode:1975PhLA...53..327S. doi:10.1016/0375-9601(75)90087-0. 
  18. ^ Castelijns, C.; Kuerten, J.; De Waele, A.; Gijsman, H. (1985). "3He flow in dilute 3He-4He mixtures at temperatures between 10 and 150 mK". Physical Review B. 32 (5). s. 2870. Bibcode:1985PhRvB..32.2870C. doi:10.1103/PhysRevB.32.2870. 
  19. ^ J.C.H. Zeegers Critical velocities and mutual friction in 3He-4He mixtures at low temperatures below 100 mK', thesis, Appendix A, Eindhoven University of Technology, 1991.
  20. ^ F. London (1938). "The λ-Phenomenon of Liquid Helium and the Bose-Einstein Degeneracy". Nature. 141 (3571). ss. 643-644. Bibcode:1938Natur.141..643L. doi:10.1038/141643a0. 
  21. ^ L. Tisza (1938). "Transport Phenomena in Helium II". Nature. 141 (3577). s. 913. Bibcode:1938Natur.141..913T. doi:10.1038/141913a0. 
  22. ^ L. Tisza (1947). "The Theory of Liquid Helium". Phys. Rev. 72 (9). ss. 838-854. Bibcode:1947PhRv...72..838T. doi:10.1103/PhysRev.72.838. 
  23. ^ Bijl, A; de Boer, J; Michels, A (1941). "Properties of liquid helium II". Physica. 8 (7). ss. 655-675. Bibcode:1941Phy.....8..655B. doi:10.1016/S0031-8914(41)90422-6. 
  24. ^ Braun, L. M., (Ed.) (2000). Selected papers of Richard Feynman with commentary. World Scientific Series in 20th century Physics. 27. World Scientific. ISBN 978-9810241315. 
  25. ^ R. P. Feynman (1954). "Atomic Theory of the Two-Fluid Model of Liquid Helium". Phys. Rev. 94 (2). s. 262. Bibcode:1954PhRv...94..262F. doi:10.1103/PhysRev.94.262. 
  26. ^ R. P. Feynman; M. Cohen (1956). "Energy Spectrum of the Excitations in Liquid Helium". Phys. Rev. 102 (5). ss. 1189-1204. Bibcode:1956PhRv..102.1189F. doi:10.1103/PhysRev.102.1189. 
  27. ^ T. D. Lee; K. Huang; C. N. Yang (1957). "Eigenvalues and Eigenfunctions of a Bose System of Hard Spheres and Its Low-Temperature Properties". Phys. Rev. 106 (6). ss. 1135-1145. Bibcode:1957PhRv..106.1135L. doi:10.1103/PhysRev.106.1135. 
  28. ^ L. Liu; L. S. Liu; K. W. Wong (1964). "Hard-Sphere Approach to the Excitation Spectrum in Liquid Helium II". Phys. Rev. 135 (5A). ss. A1166-A1172. Bibcode:1964PhRv..135.1166L. doi:10.1103/PhysRev.135.A1166. 
  29. ^ A. P. Ivashin; Y. M. Poluektov (2011). "Short-wave excitations in non-local Gross-Pitaevskii model". Cent. Eur. J. Phys. 9 (3). ss. 857-864. Bibcode:2010CEJPh.tmp..120I. doi:10.2478/s11534-010-0124-7. 
  30. ^ K. G. Zloshchastiev (2012). "Volume element structure and roton-maxon-phonon excitations in superfluid helium beyond the Gross-Pitaevskii approximation". Eur. Phys. J. B. 85 (8). s. 273. arXiv:1204.4652 $2. Bibcode:2012EPJB...85..273Z. doi:10.1140/epjb/e2012-30344-3. 
  31. ^ A. V. Avdeenkov; K. G. Zloshchastiev (2011). "Quantum Bose liquids with logarithmic nonlinearity: Self-sustainability and emergence of spatial extent". J. Phys. B: At. Mol. Opt. Phys. 44 (19). s. 195303. arXiv:1108.0847 $2. Bibcode:2011JPhB...44s5303A. doi:10.1088/0953-4075/44/19/195303. 
  32. ^ Hugh Everett, III.
  33. ^ I.I. Hirschman, Jr., A note on entropy.
  34. ^ Hau, Lene Vestergaard; Harris, S. E.; Dutton, Zachary; Behroozi, Cyrus H. (1999). "Light speed reduction to 17 metres per second in an ultracold atomic gas" (PDF). Nature. 397 (6720). s. 594. Bibcode:1999Natur.397..594V. doi:10.1038/17561. 16 Mayıs 2013 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 26 Mayıs 2016. 
  35. ^ Tanaeva, I. A. (2004). Superfluid Vortex Cooler"AIP Conference Proceedings". Cilt 710. s. 1906. doi:10.1063/1.1774894. 
  36. ^ E. Kim ve M. H. W. Chan (2004). "Probable Observation of a Supersolid Helium Phase". Nature. 427 (6971). ss. 225-227. Bibcode:2004Natur.427..225K. doi:10.1038/nature02220. PMID 14724632. 
  37. ^ Moses Chan's Research Group.
  38. ^ Sophie, A; Rittner C (2006). "Observation of Classical Rotational Inertia and Nonclassical Supersolid Signals in Solid 4 He below 250 mK". Phys. Rev. Lett. 97 (16). s. 165301. Bibcode:2006PhRvL..97p5301R. doi:10.1103/PhysRevLett.97.165301. PMID 17155406. 
  39. ^ Sophie, A; Rittner C (2007). "Disorder and the Supersolid State of Solid 4 He". Phys. Rev. Lett. 98 (17). s. 175302. arXiv:cond-mat/0702665 $2. Bibcode:2007PhRvL..98q5302R. doi:10.1103/PhysRevLett.98.175302. 
  40. ^ Boninsegni, M; Prokofev (2006). "Superglass Phase of 4 He". Phys. Rev. Lett. 96 (13). s. 135301. PMID 16711998. 
  41. ^ Pollet, L; Boninsegni M (2007). "Superfuididty of Grain Boundaries in Solid 4 He". Phys. Rev. Lett. 98 (13). s. 135301. arXiv:cond-mat/0702159 $2. Bibcode:2007PhRvL..98m5301P. doi:10.1103/PhysRevLett.98.135301. PMID 17501209. 

Konuyla ilgili yayınlar[değiştir | kaynağı değiştir]

Dış bağlantılar[değiştir | kaynağı değiştir]

"https://tr.wikipedia.org/w/index.php?title=Süperakışkan_helyum-4&oldid=32037794" sayfasından alınmıştır