Правила Фудзиты

Правила Фудзиты — набор из семи правил, формально описывающие геометрические построения с помощью плоского оригами, подобным построениям с помощью циркуля и линейки.

Фактически они описывают все возможные способы получения одной новой складки на листе бумаги, путём совмещения уже существующих различных элементов листа — точек и линий. Под линиями подразумеваются края листа или складки бумаги, под точками — пересечения линий. Существенным моментом является то, что сгиб формируется единственной складкой, причём в результате складывания фигура остается плоской.

Часто эти правила называют «аксиомами», хотя с формальной точки зрения аксиомами они не являются.

Правила[править | править код]

Складки в этих правилах существуют не всегда, правило утверждает только, что если такая складка есть, то её «можно» найти.

Правило 1[править | править код]

Пусть заданы две точки ${\displaystyle p_{1}}$ и ${\displaystyle p_{2}}$, тогда лист можно сложить так, что данные две точки будут лежать на складке.

Правило 2[править | править код]

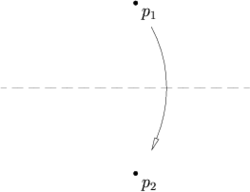
Пусть заданы две точки ${\displaystyle p_{1}}$ и ${\displaystyle p_{2}}$, тогда лист можно сложить так, что одна точка перейдёт в другую.

Правило 3[править | править код]

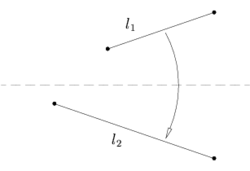
Пусть заданы две прямые ${\displaystyle l_{1}}$ и ${\displaystyle l_{2}}$, тогда лист можно сложить так, что одна прямая перейдёт в другую.

Правило 4[править | править код]

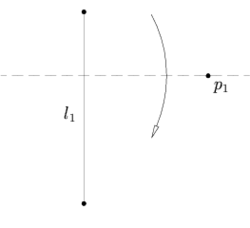
Пусть заданы прямая ${\displaystyle l_{1}}$ и точка ${\displaystyle p_{1}}$, тогда лист можно сложить так, что точка попадёт на складку, а прямая перейдёт сама в себя (то есть линия складки будет ей перпендикулярна).

Правило 5[править | править код]

Пусть заданы прямая ${\displaystyle l_{1}}$ и две точки ${\displaystyle p_{1}}$ и ${\displaystyle p_{2}}$, тогда лист можно сложить так, что точка ${\displaystyle p_{2}}$ попадёт на складку, а ${\displaystyle p_{1}}$ — на прямую ${\displaystyle l_{1}}$.

Правило 6 (складка Белок)[править | править код]

Пусть заданы две прямые ${\displaystyle l_{1}}$ и ${\displaystyle l_{2}}$ и две точки ${\displaystyle p_{1}}$ и ${\displaystyle p_{2}}$, тогда лист можно сложить так, что точка ${\displaystyle p_{1}}$ попадёт на прямую ${\displaystyle l_{1}}$, а точка ${\displaystyle p_{2}}$ попадёт на прямую ${\displaystyle l_{2}}$.

Правило 7[править | править код]

Пусть заданы две прямые ${\displaystyle l_{1}}$ и ${\displaystyle l_{2}}$ и точка ${\displaystyle p}$, тогда лист можно сложить так, что точка ${\displaystyle p}$ попадёт на прямую ${\displaystyle l_{1}}$, а прямая ${\displaystyle l_{2}}$ перейдёт сама в себя (то есть линия складки будет ей перпендикулярна).

Замечания[править | править код]

Все складки в этом списке можно получить как результат последовательного применения правила номер 6. То есть для математика они ничего не добавляют, однако позволяют уменьшить количество сгибов. Система из семи правил является полной в том смысле, что они описывают все возможные способы получения одной новой складки на листе бумаги, путём совмещения уже существующих различных элементов листа. Это последнее утверждение было доказано Лэнгом^[1].

Возможные и невозможные построения[править | править код]

Возможные[править | править код]

Все построения являются ничем иным, как решениями какого-либо уравнения, причём коэффициенты этого уравнения связаны с длинами заданных отрезков. Поэтому удобно говорить о построении числа — графического решения уравнения определенного типа. В рамках вышеописанных требований, возможны следующие построения:

• Построение решений линейных уравнений.
• Построение решений квадратных уравнений.
• Построение решений кубических уравнений (правило 6).

Иначе говоря, возможно построить лишь числа равные арифметическим выражениям с использованием квадратного и кубического корней из исходных чисел (длин отрезков). В частности, при помощи таких построений можно осуществить удвоение куба, трисекцию угла, построение правильного семиугольника.

Невозможные[править | править код]

Решение задачи о квадратуре круга однако остаётся невозможным, так как π — трансцендентное число.

История[править | править код]

Основное правило (номер 6) было рассмотрено Маргеритой Пьяцолла Белок^[2], ей же принадлежат первые построения трисекции угла и квадратуры круга с помощью оригами-построений. Складки Белок достаточно для того, чтобы получить складки во всех остальных правилах.

Полный список правил появляется в работе Жака Жюстина^[3], который позднее также ссылался на Питера Мессера как на соавтора. Практически одновременно правила 1—6 были сформулированы Фумиаки Фудзитой^[4]. Последнее седьмое правило добавил ещё позже Косиро Хатори^[5].

Вариации и обобщения[править | править код]

Список возможных построений можно значительно расширить, если позволить создание нескольких складок за один раз. Хотя человек, решивший провести несколько складок за одно действие, на практике столкнется с трудностями физического порядка, тем не менее возможно вывести правила, аналогичные правилам Фудзита и для этого случая^[6].

При допущении таких дополнительных правил, возможно доказать следующую теорему:

Любое алгебраическое уравнение степени ${\displaystyle n}$ может быть решено одновременными ${\displaystyle (n-2)}$-кратными складками .

Представляет интерес, возможно ли решить то же уравнение складыванием, вовлекающим меньшее количество одновременных складок. Это, несомненно, верно для ${\displaystyle n=4}$ и неизвестно для ${\displaystyle n=5}$^[6].

См. также[править | править код]

• Математика оригами
• Метод Лиля
• Построение с помощью циркуля и линейки

Примечания[править | править код]

Ссылки[править | править код]

• Петрунин А. Плоское оригами и построения (рус.) // Квант. — 2008. — № 1. — С. 38—40.
• Лэнг Р. Huzita Axiomas Архивная копия от 12 марта 2008 на Wayback Machine. (англ.)
• Hull T. Origami Geometric Constructions. (англ.)
• T. Hull. Solving Cubics With Creases: The Work of Beloch and Lill (англ.) // American Mathematical Monthly : journal. — 2011. — April. — P. 307—315. — doi:10.4169/amer.math.monthly.118.04.307.