Граф единичных расстояний

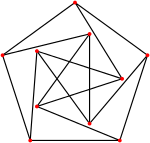
В теории графов графом единичных расстояний называется граф, образованный точками на евклидовой плоскости, при этом две вершины соединяются ребром, если расстояние между ними равно в точности единице. Рёбра графа единичных расстояний иногда пересекаются, так что они не всегда планарны. Граф единичных расстояний без пересечений называется спичечным графом.

Проблема Нелсона — Эрдёша — Хадвигера касается хроматического числа графов единичных расстояний. Известно, что существуют графы единичных расстояний, требующие 5 цветов для правильной раскраски и что все такие графы можно раскрасить не более чем в 7 цветов. Другая важная открытая задача, касающаяся графов единичных расстояний, спрашивает, сколько рёбер может иметь такой граф по отношению к числу вершин.

Примеры[править | править код]

Следующие графы являются графами единичных расстояний:

• любой цикл;
• любая решётка;
• любой граф гиперкуба;
• любая звезда;
• граф Петерсена;
• граф Хивуда (Gerbracht 2009);
• Колесо W₇;
• веретено Мозера, наименьший граф единичных расстояний с хроматическим числом 4.

Подграфы графов единичных расстояний[править | править код]

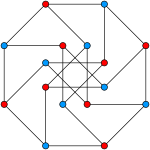
Некоторые авторы определяют граф единичных расстояний как граф, который можно вложить в плоскость так, что любые две смежные вершины должны находиться на расстоянии единица, но не обязательно вершины, находящиеся на расстоянии единица, должны быть смежными. Например граф Мёбиуса-Кантора имеет графическое представление такого вида.

Согласно такому определению все обобщённые графы Петерсена являются графами единичных расстояний (Žitnik, Horvat, Pisanski 2010). Чтобы различать эти два определения, графы, у которых любые две вершины, находящиеся на расстоянии единица, соединены ребром, будем называть строгими графами единичных расстояний (Gervacio, Lim, Maehara 2008).

Граф, образованный удалением одной спицы из колеса W₇, является подграфом единичных расстояний, но не строгим графом единичных расстояний(Soifer 2008, С. 94).

Подсчёт единичных расстояний[править | править код]

Нерешённые проблемы математики: Сколько единичных расстояний может быть в множестве из n точек?

Эрдёш (Erdős 1946) предложил задачу оценки в множестве из n точек числа пар, находящихся на расстоянии единицы. В терминах теории графов вопрос состоит в оценке плотности графа единичных расстояний.

Граф гиперкуба даёт нижнюю границу числа единичных расстояний, пропорциональную ${\displaystyle n\log n.}$ Рассматривая точки квадратной решётки с тщательно выбранным расстоянием, Эрдёш нашёл улучшенную нижнюю границу

${\displaystyle n^{1+c/\log \log n},}$

и предложил премию в 500 долл. за выяснение, выражается ли максимальное число единичных расстояний функцией того же вида (Kuperberg 1992). Лучшая известная верхняя граница, согласно Спенсеру, Семереди и Троттеру (Spencer, Szemerédi, Trotter 1984), пропорциональна

${\displaystyle n^{4/3};}$.

Эту границу можно рассматривать как число попаданий точек на единичные окружности и она тесно связана с теоремой Семереди — Троттера об инцидентности точек и прямых.

Представление алгебраических чисел и теорема Бекмана-Куорлса[править | править код]

Для любого алгебраического числа A можно найти граф единичных расстояний G, в котором некоторые пары вершин находятся на расстоянии A во всех представлениях с единичными расстояниями G (Maehara 1991) (Maehara 1992). Этот результат подразумевает конечную версию теоремы Бекмана–Куорлса^[en] —для любых двух точек p и q, находящихся на расстоянии A, существует конечный жёсткий^[en] граф единичных расстояний, содержащий p и q такой, что любое преобразование плоскости, сохраняющее единичные расстояния в этом графе сохраняет расстояние между p и q (Tyszka 2000). Полная теорема Бекмана — Куорлса утверждает, что любое преобразование евклидовой плоскости (или пространства большей размерности), сохраняющее расстояния должно быть конгруэнцией. Таким образом для бесконечных графов единичных расстояний, вершинами которых является вся плоскость, любой автоморфизм графа должен быть изометрией (Beckman, Quarles 1953).

Обобщение на большие размерности[править | править код]

Определение графа единичных расстояний может быть естественным образом обобщено на любую размерность евклидового пространства. Любой граф можно вложить в виде набора точек в пространство достаточно высокой размерности. Маэхара и Рёдль (Maehara, Rödl 1990) показали, что размерность, необходимая для вложения графа, может быть ограничена удвоенной максимальной степенью.

Необходимая для вложения графа размерность, при котором все рёбра будут иметь единичную длину, и размерность вложения, при котором рёбра будут соединять в точности те точки, между которыми расстояние единица, могут существенно отличаться. Корону с 2n вершинами можно вложить в четырёхмерное пространство так, что все рёбра будут иметь единичную дину, но требуется по меньшей мере размерность n − 2, чтобы вложить так, что не будет пар вершин, находящихся на расстоянии единица, не соединённых ребром (Erdős, Simonovits 1980).

Вычислительная сложность[править | править код]

Является NP-трудной задачей, точнее полной для теории существования вещественных чисел, проверить, является ли данный граф графом единичных расстояний или строгим графом единичных расстояний (Schaefer 2013).

См. также[править | править код]

• Граф единичных кругов, граф на плоскости, у которого две вершины соединены ребром, если расстояние между точками не превосходит единицы.

Примечания[править | править код]

• F. S. Beckman, D. A., Jr. Quarles. On isometries of Euclidean spaces // Proceedings of the American Mathematical Society. — 1953. — Т. 4. — С. 810—815.
• Paul Erdős. On sets of distances of n points. — American Mathematical Monthly. — The American Mathematical Monthly, 1946. — Т. 53. — С. 248—250. — doi:10.2307/2305092..
• Paul Erdős, Miklós Simonovits. On the chromatic number of geometric graphs // Ars Combinatoria. — 1980. — Т. 9. — С. 229—246. Как цитировано в Soifer, 2008, p. 97.
• Eberhard H.-A. Gerbracht. Eleven unit distance embeddings of the Heawood graph. — 2009. — arXiv:0912.5395..
• Severino V. Gervacio, Yvette F. Lim, Hiroshi Maehara. Planar unit-distance graphs having planar unit-distance complement // Discrete Mathematics. — 2008. — Т. 308, вып. 10. — С. 1973—1984. — doi:10.1016/j.disc.2007.04.050..
• Greg Kuperberg. The Erdos kitty: At least $9050 in prizes!. — 1992. Архивировано 29 сентября 2006 года.
• Hiroshi Maehara. Distances in a rigid unit-distance graph in the plane // Discrete Applied Mathematics. — 1991. — Т. 31, вып. 2. — С. 193—200. — doi:10.1016/0166-218X(91)90070-D..
• Hiroshi Maehara. Extending a flexible unit-bar framework to a rigid one // Discrete Mathematics. — 1992. — Т. 108, вып. 1-3. — С. 167—174. — doi:10.1016/0012-365X(92)90671-2..
• Hiroshi Maehara, Vojtech Rödl. On the dimension to represent a graph by a unit distance graph // Graphs and Combinatorics. — 1990. — Т. 6, вып. 4. — С. 365—367. — doi:10.1007/BF01787703..
• Marcus Schaefer. Thirty Essays on Geometric Graph Theory / János Pach. — Springer, 2013. — С. 461—482. — doi:10.1007/978-1-4614-0110-0_24..
• Alexander Soifer. The Mathematical Coloring Book. — Springer-Verlag, 2008. — ISBN 978-0-387-74640-1.
• Joel Spencer, Endre Szemerédi, William T. Trotter. Graph Theory and Combinatorics. — Academic Press, 1984. — С. 293—308.
• Apoloniusz Tyszka. Discrete versions of the Beckman-Quarles theorem // Aequationes Mathematicae. — 2000. — Т. 59, вып. 1—2. — С. 124—133. — doi:10.1007/PL00000119..
• Arjana Žitnik, Boris Horvat, Tomaž Pisanski. All generalized Petersen graphs are unit-distance graphs. — 2010. — Т. 1109.

Ссылки[править | править код]

• Suresh Venkatasubramanian. Problem 39: Distances among Point Sets in R² and R³ // The Open Problems Project. Архивировано 30 августа 2006 года.
• Weisstein, Eric W. Unit-Distance Graph (англ.) на сайте Wolfram MathWorld.

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. После исправления проблемы исключите её из списка. Удалите шаблон, если устранены все недостатки.