Heap binomial

Em ciência da computação, um heap binomial é um tipo de heap semelhante a um heap binário, mas que também suporta a rápida união entre duas heaps. Isso é conseguido através do uso de uma estrutura de árvore especial. Ela é importante como uma implementação da mergeable heap (tipo abstrato de dado), que é uma fila de prioridade que suporta a operação de merge.
Heap binomial[editar | editar código-fonte]
Um heap binomial é implementado como uma coleção de árvores binomiais (compare com um heap binário, que tem a forma de uma única árvore binária), que são definidos recursivamente da seguinte forma:
- Uma árvore binomial de ordem 0 é um único nó
- Uma árvore binomial de ordem k tem um nó raiz cujos filhos são raízes de árvores binomiais de ordens k-1, k-2, ..., 2, 1, 0 (nesta ordem).

Uma árvore binomial de ordem k tem 2k nós, e altura k.
Devido a sua estrutura singular, uma árvore binomial de ordem k pode ser construída a partir de duas árvores de ordem k-1 trivialmente, anexando uma delas como filho mais à esquerda da raiz da outra árvore. Este recurso é fundamental para a operação de merge em um heap binomial, que é a sua maior vantagem sobre as outras heaps convencionais.
O nome vem da forma: uma árvore binomial de ordem tem nós em profundidade . (Ver coeficiente binomial.)
Estrutura de um heap binomial[editar | editar código-fonte]
Um heap binomial é implementado como um conjunto de árvores binomiais que satisfazem as propriedades do heap binomial:
- Cada árvore binomial em um heap obedece à propriedade do min-heap: a chave de um nó é maior que ou igual a chave de seu pai.
- Só pode haver uma ou zero árvores binomiais para cada ordem, inclusive a ordem zero.
A primeira propriedade garante que a raiz de cada árvore binomial contém a menor chave na árvore, que se aplica a todo o heap.
A segunda propriedade implica que um heap binomial com n nós consiste em no máximo log n + 1 árvores binomiais. Na verdade, os números e ordens destas árvores são exclusivamente determinados pelo número de nós n: cada árvore binomial corresponde a um dígito na representação binária de número n. Por exemplo, o número 13 é 1101 em binário, e, assim, um heap binomial com 13 nós será composto de três árvores binomiais de ordens 3, 2, e 0 (ver figura abaixo).

Exemplo de um heap binomial contendo 13 nós com chaves diferentes.
Implementação[editar | editar código-fonte]
Devido ao fato que nenhuma operação que requer acesso aleatório para os nós raiz da árvore binomial, as raízes das árvores binomiais podem ser armazenados em uma lista ligada, ordenados pela ordem da árvore de forma crescente.
Merge[editar | editar código-fonte]

Como mencionado acima, a mais simples e mais importante operação é a fusão de duas árvores binomiais de mesma ordem dentro de um heap binomial. Devido à estrutura das árvores binomiais, eles podem ser mescladas trivialmente. Como o nó raiz é o menor elemento da árvore, comparando-se as duas chaves, o menor deles é a chave mínima, que se torna o novo nó raiz. Em seguida, a outra árvore torna-se uma subárvore da árvore mesclada. Esta operação é básica para a completa fusão entre dois heaps binomiais.
função mergeArvore(p, q) se p.raiz.chave <= q.raiz.chave retorne p.addSubArvore(q) senão retorne p.addSubArvore(p)
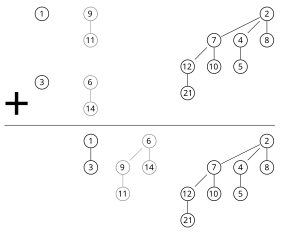
A operação de fusão de duas heaps é, talvez, a mais interessante e pode ser usada como uma sub-rotina na maioria das outras operações. As listas de raízes de ambas as heaps são percorridas simultaneamente de uma maneira semelhante ao algoritmo de merge.
Se apenas um dos heaps contém uma árvore de ordem j, esta árvore é movida para o heap mesclado. Se ambas as heaps contêm uma árvore de ordem j, as duas árvores são mescladas para uma árvore de ordem j+1, de modo que a propriedade de min-heap é satisfeita. Note que pode ser necessário mais tarde mesclar esta árvore com outra árvore de ordem j+1 presente em uma das heaps. No decorrer do algoritmo, precisamos examinar mais de três árvores de qualquer ordem (duas de dois heaps mesclados e outro composto de duas pequenas árvores).
Porque cada árvore binomial em um heap binomial corresponde a um bit na representação binária do seu tamanho, há uma analogia entre a fusão de duas heaps e a adição binária dos tamanhos das duas heaps, a partir da direita-para-esquerda. Sempre que um transporte ocorre durante a adição, isto corresponde a uma fusão de duas árvores binomiais durante a fusão.
Cada árvore tem ordem de, no máximo log n e, portanto, o tempo de execução é O(log n).
function merge(p, q) while not (p.end() and q.end()) tree = mergeTree(p.currentTree(), q.currentTree())
if not heap.currentTree().empty() tree = mergeTree(tree, heap.currentTree())
heap.addTree(tree) heap.next(); p.next(); q.next()
Inserção[editar | editar código-fonte]
A inserção de um novo elemento em um heap pode ser feito simplesmente pela criação de uma nova heap contendo apenas este elemento e, em seguida, mesclando-o com o heap original. Devido à mesclagem, inserir leva O(log n) em tempo. No entanto, através de uma série de n inserções consecutivas, a inserção tem um tempo amortizado de O(1) (constante).
Encontrar mínimo[editar | editar código-fonte]
Para encontrar o mínimo elemento do heap, encontre o mínimo entre as raízes das árvores binomiais. Isso novamente pode facilmente ser feito em tempo O(log n), pois há apenas O(log n) árvores e, portanto, raízes para examinar.
Usando um ponteiro para a árvore binomial que contém o elemento mínimo, o tempo para esta operação pode ser reduzido para O(1). O ponteiro deve ser atualizado sempre na execução de qualquer operação diferente de Encontrar o mínimo. Isso pode ser feito em O(log n) sem aumentar o tempo de execução de qualquer operação.
Excluir mínimo[editar | editar código-fonte]
Para excluir o mínimo elemento do heap, primeiro encontre este elemento, remova-o de sua árvore binomial, e obtenha uma lista de suas subárvores. Em seguida, transforme esta lista de subárvores em uma heap binomial separada, reordenando-as da menor para a maior ordem. Em seguida, mescle esse heap com o heap original. Uma vez que cada raiz tem no máximo log n filhos, criar esta nova heap é O(log n). A fusão das heaps é O(log n), de modo que toda a operação de excluir o mínimo é O(log n).
function deleteMin(heap) min = heap.trees().first() for each current in heap.trees() if current.root < min.root then min = current for each tree in min.subTrees() tmp.addTree(tree) heap.removeTree(min) merge(heap, tmp)
Diminuir chave[editar | editar código-fonte]
Ao diminuir a chave de um elemento, ele pode se tornar menor do que a chave de seu pai, violando a propriedade de min-heap. Se este for o caso, troque o elemento com seu pai, e, possivelmente também com seus avós, e assim por diante, até que a propriedade de min-heap não seja violada. Cada árvore binomial tem altura de no máximo, log n, de modo que isso leva O(log n) em tempo.
Remoção[editar | editar código-fonte]
Para remover um elemento do heap, diminua a sua chave para o infinito negativo (isto é, um valor menor do que qualquer elemento na heap) e em seguida elimine o valor mínimo na heap.
Resumo dos tempos de execução[editar | editar código-fonte]
Nas seguintes complexidades de tempo[1] O(f) é um limite assintótico superior e Θ(f) é um limite assintótico estreito (ver Notação Big O). Os nomes das funções assumem que é um min-heap.
| Operação | Binária[1] | Binomial[1] | Fibonacci[1][2] | Brodal[3][a] |
|---|---|---|---|---|
| encontrar-min | Θ(1) | Θ(log n) | Θ(1) | Θ(1) |
| remover-min | Θ(log n) | Θ(log n) | O(log n)[b] | O(log n) |
| inserção | O(log n) | Θ(1)[b] | Θ(1) | Θ(1) |
| diminuir-chave | Θ(log n) | Θ(log n) | Θ(1)[b] | Θ(1) |
| merge | Θ(n) | O(log n)[c] | Θ(1) | Θ(1) |
Aplicações[editar | editar código-fonte]
Ver também[editar | editar código-fonte]
Referências
- ↑ a b c d Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L. Introduction to Algorithms. [S.l.]: MIT Press and McGraw-Hill
- ↑ Fredman, Michael Lawrence; Tarjan, Robert E. «Fibonacci heaps and their uses in improved network optimization algorithms» (PDF). July 1987. Journal of the Association for Computing Machinery. 34 (3): 596–615. doi:10.1145/28869.28874
- ↑ Brodal, Gerth S. (1996), «Worst-Case Efficient Priority Queues» (PDF), Proc. 7th Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 52–58
- ↑ Goodrich, Michael T.; Tamassia, Roberto (2004). «7.3.6. Bottom-Up Heap Construction». Data Structures and Algorithms in Java 3rd ed. [S.l.: s.n.] pp. 338–341. ISBN 0-471-46983-1
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L. Introduction to Algorithms. [S.l.]: MIT Press and McGraw-Hill
- 21. doi:10.1145/359460.359478
Ligações externas[editar | editar código-fonte]
- Java applet simulation of binomial heap
- Python implementation of binomial heap
- Two C implementations of binomial heap (a generic one and one optimized for integer keys)
- Haskell implementation of binomial heap
- Common Lisp implementation of binomial heap



