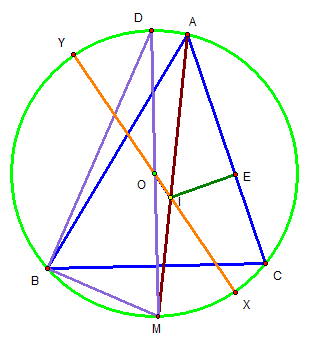
 오일러 삼각형 정리와 그에 필요한 보조선, 보조점들
오일러 삼각형 정리와 그에 필요한 보조선, 보조점들 기하학에서 오일러 삼각형 정리(Euler三角形定理, 영어: Euler's triangle theorem)는 삼각형의 외심과 내심 사이의 거리를 외접원과 내접원의 반지름을 통해 나타내는 정리이다.
주어진 삼각형의 외접원의 반지름을  , 내접원의 반지름을
, 내접원의 반지름을  라고 하고, 외심과 내심 사이의 거리를
라고 하고, 외심과 내심 사이의 거리를  라고 하자. 오일러 삼각형 정리에 따르면, 다음이 성립한다.
라고 하자. 오일러 삼각형 정리에 따르면, 다음이 성립한다.

특히, 다음과 같은 부등식이 성립한다.

이 부등식에서 등호가 성립할 필요충분조건은 정삼각형이다.
삼각형  의 외심을
의 외심을  , 내심을
, 내심을  라고 하고,
라고 하고,  를 지나는 외접원의 지름을
를 지나는 외접원의 지름을  라고 하자.
라고 하자.  의 이등분선의 연장선과 외접원의 교점을
의 이등분선의 연장선과 외접원의 교점을  이라고 하고,
이라고 하고,  의 연장선과 외접원의 교점을
의 연장선과 외접원의 교점을  라고 하자.
라고 하자.  를 지나는
를 지나는  의 수선의 발을
의 수선의 발을  라고 하자. 그렇다면 방멱 정리에 의하여
라고 하자. 그렇다면 방멱 정리에 의하여

이며, 또한 맨션 정리에 의하여  이다. 삼각형
이다. 삼각형  와
와  을 생각할 때, 호
을 생각할 때, 호  의 원주각의 성질에 의하여
의 원주각의 성질에 의하여

이고,  은 지름이므로
은 지름이므로

이다. 따라서 이 두 삼각형은 서로 닮음이며, 특히

가 성립한다. 이 결과들을 연립하면

를 얻는다.


























