브레젠험 직선 알고리즘

브레젠험 직선 알고리즘(Bresenham's line algorithm)은 래스터의 n차원 직선이 두 점 사이의 직선에 대한 근사값을 형성하기 위해 선택되어야 하는 점들을 결정하는 선 그리기 알고리즘이다. 이는 역사적으로 일반적인 컴퓨터 아키텍처에서 매우 저렴한 연산인 정수 덧셈, 뺄셈, 비트 시프팅만을 사용하기 때문에 비트맵 이미지(예: 컴퓨터 화면)에 선 기본 도형을 그리는 데 일반적으로 사용된다. 이는 점진적 오류 알고리즘이며, 컴퓨터 그래픽스 분야에서 개발된 초기 알고리즘 중 하나이다. 원래 알고리즘을 확장한 중점 원 알고리즘은 원을 그리는 데 사용할 수 있다.

우 알고리즘과 같은 알고리즘은 계단 현상 제거를 지원할 수 있기 때문에 최신 컴퓨터 그래픽스에서 자주 사용되지만, 브레젠험 직선 알고리즘은 속도와 단순성 때문에 여전히 중요하다. 이 알고리즘은 플로터와 같은 하드웨어와 최신 그래픽 카드의 그래픽 처리 장치에 사용된다. 또한 많은 소프트웨어 그래픽스 라이브러리에서도 찾을 수 있다. 알고리즘이 매우 간단하기 때문에 최신 그래픽 카드의 펌웨어 또는 그래픽 하드웨어에 자주 구현된다.

오늘날 "브레젠험"이라는 명칭은 브레젠험의 원래 알고리즘을 확장하거나 수정한 알고리즘 계열에 사용된다.

브레젠험 직선 알고리즘은 1962년 IBM에서 이 알고리즘을 개발한 잭 엘턴 브레젠험의 이름을 따서 명명되었다. 2001년에 브레젠험은 다음과 같이 썼다.^[1]

나는 IBM 샌호세 개발 연구소의 계산실에서 일하고 있었다. 칼콤프 플로터(Calcomp plotter)가 1407 타자기 콘솔을 통해 IBM 1401에 연결되었다. [알고리즘]은 1962년 여름에, 아마 한 달 정도 전에 생산에 사용되었다. 당시 프로그램은 기업 간에 자유롭게 교환되었기 때문에 칼콤프(짐 뉴랜드 및 캘빈 헤프테)에는 사본이 있었다. 1962년 가을에 스탠포드로 돌아왔을 때 스탠포드 컴퓨터 센터 라이브러리에 사본을 넣었다. 선 그리기 루틴에 대한 설명은 콜로라도 덴버에서 열린 1963년 ACM 전국 컨벤션에서 발표 승인을 받았다. 그 해에는 논문집이 출판되지 않고 커뮤니케이션스 오브 더 ACM에 발표자와 주제 목록만 실렸다. IBM 시스템스 저널의 한 사람이 제 발표 후 논문을 실을 수 있는지 물었다. 나는 기꺼이 동의했고, 그들은 1965년에 논문을 인쇄했다.

다음 규칙이 적용된다.

• 왼쪽 상단은 (0,0)으로, 픽셀 좌표는 오른쪽 및 아래쪽 방향으로 증가한다 (예를 들어, (7,4)의 픽셀은 (7,5)의 픽셀 바로 위에 있다).
• 픽셀 중심은 정수 좌표를 갖는다.

선의 끝점은 ${\displaystyle (x_{0},y_{0})}$ 및 ${\displaystyle (x_{1},y_{1})}$의 픽셀이며, 쌍의 첫 번째 좌표는 열이고 두 번째 좌표는 행이다.

알고리즘은 처음에 선분이 아래쪽과 오른쪽으로 가는 팔분원(${\displaystyle x_{0}\leq x_{1}}$ 및 ${\displaystyle y_{0}\leq y_{1}}$)에 대해서만 제시되며, 그 수평 투영 ${\displaystyle x_{1}-x_{0}}$은 수직 투영 ${\displaystyle y_{1}-y_{0}}$보다 길다(선은 1보다 작은 양의 기울기를 갖는다). 이 팔분원에서 ${\displaystyle x_{0}}$과 ${\displaystyle x_{1}}$ 사이의 각 열 x에 대해 선의 픽셀을 포함하는 행 y(알고리즘으로 계산됨)가 정확히 하나 있는 반면, ${\displaystyle y_{0}}$과 ${\displaystyle y_{1}}$ 사이의 각 행은 여러 래스터화된 픽셀을 포함할 수 있다.

브레젠험 알고리즘은 동일한 x에 대한 이상적인(분수) y에 가장 가까운 픽셀 중심에 해당하는 정수 y를 선택한다. 연속적인 열에서 y는 동일하게 유지되거나 1만큼 증가할 수 있다. 끝점을 통과하는 선의 일반 방정식은 다음과 같다.

${\displaystyle {\frac {y-y_{0}}{y_{1}-y_{0}}}={\frac {x-x_{0}}{x_{1}-x_{0}}}}$.

열 x를 알고 있으므로 픽셀의 행 y는 이 양을 가장 가까운 정수로 반올림하여 구할 수 있다.

${\displaystyle y={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}(x-x_{0})+y_{0}}$.

기울기 ${\displaystyle (y_{1}-y_{0})/(x_{1}-x_{0})}$는 끝점 좌표에만 의존하며 미리 계산할 수 있으며, ${\displaystyle y_{0}}$에서 시작하여 반복적으로 기울기를 더하여 연속적인 정수 x 값에 대한 이상적인 y를 계산할 수 있다.

실제적으로 알고리즘은 y 좌표를 추적하지 않는데, 이는 x가 1씩 증가할 때마다 m = ∆y/∆x씩 증가한다. 알고리즘은 각 단계에서 오류 경계를 유지하며, 이는 (a) 선이 픽셀을 벗어나는 지점부터 (b) 픽셀의 상단 가장자리까지의 거리의 음수 값을 나타낸다. 이 값은 처음에 ${\displaystyle y_{0}-0.5}$로 설정되며(픽셀의 중심 좌표를 사용하기 때문에), x 좌표가 1씩 증가할 때마다 m만큼 증가한다. 오류가 0.5보다 커지면 선이 위쪽으로 한 픽셀 이동했고 y 좌표를 증가시키고 새 픽셀 상단으로부터의 거리를 나타내도록 오류를 조정해야 한다는 것을 알 수 있다. 이는 오류에서 1을 빼서 수행한다.^[2]

브레젠험 알고리즘을 도출하기 위해서는 두 단계를 거쳐야 한다. 첫 번째 단계는 선의 방정식을 전형적인 기울기-절편 형태에서 다른 형태로 변환하는 것이고, 그 다음에는 이 새로운 방정식을 사용하여 오류 누적 아이디어를 기반으로 선을 그리는 것이다.

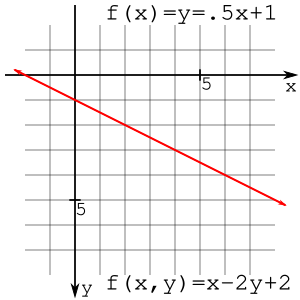
선의 기울기-절편 형태는 다음과 같이 쓰여진다.

${\displaystyle y=f(x)=mx+b}$

여기서 ${\displaystyle m}$은 기울기이고 ${\displaystyle b}$는 y 절편이다. 이것은 ${\displaystyle x}$만의 함수이기 때문에 수직선을 표현할 수 없다. 따라서 이 방정식을 ${\displaystyle x}$와 ${\displaystyle y}$ 모두의 함수로 작성하여 어떤 각도의 선도 그릴 수 있도록 하는 것이 유용할 것이다. 선의 각도(또는 기울기)는 "rise over run" 또는 ${\displaystyle \Delta y/\Delta x}$로 표현될 수 있다. 그런 다음 대수적 조작을 사용하여

${\displaystyle {\begin{aligned}y&=mx+b\\y&={\frac {\Delta y}{\Delta x}}x+b\\(\Delta x)y&=(\Delta y)x+(\Delta x)b\\0&=(\Delta y)x-(\Delta x)y+(\Delta x)b\end{aligned}}}$

이 마지막 방정식을 ${\displaystyle x}$와 ${\displaystyle y}$의 함수로 만들면 다음과 같이 쓸 수 있다.

${\displaystyle f(x,y):=Ax+By+C=0}$

여기서 상수는 다음과 같다.

• ${\displaystyle A=\Delta y=y_{1}-y_{0}}$
• ${\displaystyle B=-\Delta x=-(x_{1}-x_{0})}$
• ${\displaystyle C=(\Delta x)b=(x_{1}-x_{0})b}$

그러면 선은 ${\displaystyle f(x,y)=0}$인 곳에서 어떤 상수 ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$에 대해 정의된다. 즉, 선 위에 있지 않은 모든 ${\displaystyle (x,y)}$에 대해 ${\displaystyle f(x,y)\neq 0}$이다. 이 형태는 ${\displaystyle x}$와 ${\displaystyle y}$가 정수인 경우 정수만 포함한다. 왜냐하면 상수 ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$는 정수로 정의되기 때문이다.

예를 들어, 선 ${\textstyle y={\frac {1}{2}}x+1}$은 ${\displaystyle f(x,y)=x-2y+2}$로 쓸 수 있다. 점 (2,2)는 선 위에 있다.

${\displaystyle f(2,2)=x-2y+2=(2)-2(2)+2=2-4+2=0}$

그리고 점 (2,3)은 선 위에 있지 않다.

${\displaystyle f(2,3)=(2)-2(3)+2=2-6+2=-2}$

그리고 점 (2,1)도 마찬가지이다.

${\displaystyle f(2,1)=(2)-2(1)+2=2-2+2=2}$

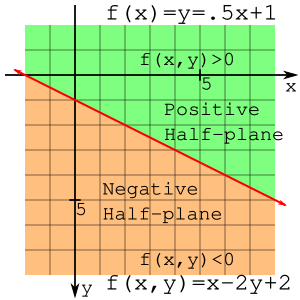
(2,1)과 (2,3)은 선의 반대편에 있으며 ${\displaystyle f(x,y)}$는 양수 또는 음수로 평가된다는 점에 유의하라. 선은 평면을 반으로 나누며, ${\displaystyle f(x,y)}$가 음수인 반평면을 음수 반평면, 다른 반평면을 양수 반평면이라고 할 수 있다. 이 관찰은 나머지 도출에서 매우 중요하다.

시작점은 선 위에 있다.

${\displaystyle f(x_{0},y_{0})=0}$

이는 선이 정수 좌표에서 시작하고 끝나는 것으로 정의되기 때문만은 아니다(비정수 끝점을 갖는 선을 그리려는 것도 전적으로 합리적이다).

기울기가 최대 ${\displaystyle 1}$이라는 점을 염두에 두고, 이제 다음 점이 ${\displaystyle (x_{0}+1,y_{0})}$이 되어야 하는지 또는 ${\displaystyle (x_{0}+1,y_{0}+1)}$이 되어야 하는지에 대한 문제가 제기된다. 아마도 직관적으로 점은 ${\displaystyle x_{0}+1}$에서 선에 더 가까운 점에 따라 선택되어야 할 것이다. 전자에 더 가깝다면 전자를 선에 포함시키고, 후자라면 후자를 포함시킨다. 이를 답하기 위해 이 두 점 사이의 중간점에서 선 함수를 평가한다.

${\displaystyle f(x_{0}+1,y_{0}+{\tfrac {1}{2}})}$

이 값의 값이 양수이면 이상적인 선은 중간점 아래에 있고 후보 점 ${\displaystyle (x_{0}+1,y_{0}+1)}$에 더 가깝다. 즉, y 좌표는 증가해야 한다. 그렇지 않으면 이상적인 선이 중간점을 통과하거나 그 위에 있으며 y 좌표는 동일하게 유지되어야 한다. 이 경우 점 ${\displaystyle (x_{0}+1,y_{0})}$이 선택된다. 이 중간점에서 선 함수 값은 어떤 점을 선택해야 하는지를 결정하는 유일한 요소이다.

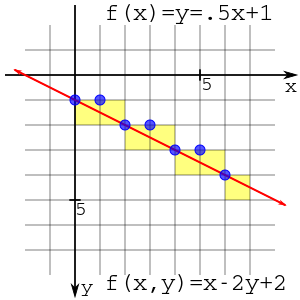
인접한 이미지는 파란색 점 (2,2)이 녹색 후보 점 (3,2) 및 (3,3)과 함께 선 위에 있는 것으로 선택되었음을 보여준다. 검은색 점 (3, 2.5)는 두 후보 점 사이의 중간점이다.

대신, 중간점에서 f(x,y)를 평가하는 대신 점 간의 차이를 사용할 수 있다. 이 대안 방법은 정수 전용 산술을 허용하며, 이는 일반적으로 부동 소수점 산술보다 빠르다. 다른 방법을 도출하기 위해 차이를 다음과 같이 정의한다.

${\displaystyle D_{i}=f(x_{i}+1,y_{i}+{\tfrac {1}{2}})-f(x_{0},y_{0})}$

첫 번째 결정에 대해 이 공식화는 시작점에서 ${\displaystyle f(x_{0},y_{0})=0}$이므로 중간점 방법과 동일하다. 이 표현을 단순화하면 다음과 같다.

${\displaystyle {\begin{array}{rclcl}D_{0}&=&\left[A(x_{0}+1)+B\left(y_{0}+{\frac {1}{2}}\right)+C\right]&-&\left[Ax_{0}+By_{0}+C\right]\\&=&\left[Ax_{0}+By_{0}+C+A+{\frac {1}{2}}B\right]&-&\left[Ax_{0}+By_{0}+C\right]\\&=&A+{\frac {1}{2}}B=\Delta y-{\frac {1}{2}}\Delta x\end{array}}}$

중간점 방법과 마찬가지로 ${\displaystyle D_{0}}$가 양수이면 ${\displaystyle (x_{0}+1,y_{0}+1)}$를 선택하고, 그렇지 않으면 ${\displaystyle (x_{0}+1,y_{0})}$를 선택한다.

만약 ${\displaystyle (x_{0}+1,y_{0})}$가 선택되면 ${\displaystyle D_{i}}$의 변화는 다음과 같다.

${\displaystyle {\begin{array}{lclcl}\Delta D&=&f(x_{0}+2,y_{0}+{\tfrac {1}{2}})-f(x_{0}+1,y_{0}+{\tfrac {1}{2}})&=&A&=&\Delta y\\\end{array}}}$

만약 ${\displaystyle (x_{0}+1,y_{0}+1)}$가 선택되면 ${\displaystyle D_{i}}$의 변화는 다음과 같다.

${\displaystyle {\begin{array}{lclcl}\Delta D&=&f(x_{0}+2,y_{0}+{\tfrac {3}{2}})-f(x_{0}+1,y_{0}+{\tfrac {1}{2}})&=&A+B&=&\Delta y-\Delta x\end{array}}}$

새로운 D가 양수이면 ${\displaystyle (x_{0}+2,y_{0}+1)}$가 선택되고, 그렇지 않으면 ${\displaystyle (x_{0}+2,y_{0})}$가 선택된다. 이 결정은 각 후속 지점에 오류를 누적함으로써 일반화될 수 있다.

알고리즘의 모든 도출이 완료되었다. 한 가지 성능 문제는 D의 초기 값에 1/2 요인이 있다는 것이다. 이 모든 것이 누적된 차이의 부호에 관한 것이므로 모든 것을 2로 곱해도 아무런 결과가 없다.

그 결과 정수 산술만 사용하는 알고리즘이 만들어진다.

plotLine(x0, y0, x1, y1)     dx = x1 - x0     dy = y1 - y0     D = 2*dy - dx     y = y0 

    for x from x0 to x1         plot(x, y)         if D > 0             y = y + 1             D = D - 2*dx         end if         D = D + 2*dy 

${\displaystyle f(x,y)=x-2y+2}$를 (0,1)에서 (6,4)까지 이 알고리즘을 실행하면 dx=6 및 dy=3으로 다음과 같은 차이가 발생한다.

D=2*3-6=0 Loop from 0 to 6  * x=0: plot(0, 1), D≤0: D=0+6=6  * x=1: plot(1, 1), D>0: D=6-12=-6, y=1+1=2, D=-6+6=0  * x=2: plot(2, 2), D≤0: D=0+6=6  * x=3: plot(3, 2), D>0: D=6-12=-6, y=2+1=3, D=-6+6=0  * x=4: plot(4, 3), D≤0: D=0+6=6  * x=5: plot(5, 3), D>0: D=6-12=-6, y=3+1=4, D=-6+6=0  * x=6: plot(6, 4), D≤0: D=0+6=6 

이 플롯의 결과는 오른쪽에 표시된다. 플롯은 선 교차점(파란색 원)에 플롯하거나 픽셀 상자(노란색 사각형)를 채워서 볼 수 있다. 상관없이 플롯은 동일하다.

그러나 위에서 언급했듯이 이것은 팔분원 0, 즉 원점에서 시작하여 기울기가 0에서 1 사이이며 x가 반복당 정확히 1씩 증가하고 y가 0 또는 1씩 증가하는 선에만 작동한다.

알고리즘은 y가 증가해야 하는지 감소해야 하는지(즉, dy < 0) 확인하여 기울기가 0에서 -1 사이를 포함하도록 확장될 수 있다.

plotLineLow(x0, y0, x1, y1)     dx = x1 - x0     dy = y1 - y0     yi = 1     if dy < 0         yi = -1         dy = -dy     end if     D = (2 * dy) - dx     y = y0 

    for x from x0 to x1         plot(x, y)         if D > 0             y = y + yi             D = D + (2 * (dy - dx))         else             D = D + 2*dy         end if 

x 및 y 축을 전환함으로써 양수 또는 음수의 가파른 기울기에 대한 구현은 다음과 같이 작성할 수 있다.

plotLineHigh(x0, y0, x1, y1)     dx = x1 - x0     dy = y1 - y0     xi = 1     if dx < 0         xi = -1         dx = -dx     end if     D = (2 * dx) - dy     x = x0 

    for y from y0 to y1         plot(x, y)         if D > 0             x = x + xi             D = D + (2 * (dx - dy))         else             D = D + 2*dx         end if 

완전한 솔루션은 x1 > x0 또는 y1 > y0인지 감지하고 그리기 전에 입력 좌표를 역전시켜야 한다.

plotLine(x0, y0, x1, y1)     if abs(y1 - y0) < abs(x1 - x0)         if x0 > x1             plotLineLow(x1, y1, x0, y0)         else             plotLineLow(x0, y0, x1, y1)         end if     else         if y0 > y1             plotLineHigh(x1, y1, x0, y0)         else             plotLineHigh(x0, y0, x1, y1)         end if     end if 

비디오 메모리에 직접 액세스하는 저수준 구현에서는 수직 및 수평선의 특수한 경우를 별도로 처리하는 것이 일반적이다. 매우 최적화될 수 있기 때문이다.

일부 버전은 브레젠험의 정수 증분 오류 원리를 사용하여 x 및 y 좌표 사이의 양수 및 음수 오류 균형을 맞춰 모든 팔분 선 그리기를 수행한다.^[3]

plotLine(x0, y0, x1, y1)     dx = abs(x1 - x0)     sx = x0 < x1 ? 1 : -1     dy = -abs(y1 - y0)     sy = y0 < y1 ? 1 : -1     error = dx + dy 

    while true         plot(x0, y0)         e2 = 2 * error         if e2 >= dy             if x0 == x1 break             error = error + dy             x0 = x0 + sx         end if         if e2 <= dx             if y0 == y1 break             error = error + dx             y0 = y0 + sy         end if     end while 

브레젠험 알고리즘은 약간 수정된 디지털 미분 분석기(겹치지 않는 다각형 래스터링에 필요한 0 대신 0.5를 오류 임계값으로 사용)로 해석될 수 있다.

나눗셈 연산 대신 점진적 오류를 사용하는 원리는 그래픽스에서 다른 응용 프로그램을 갖는다. 이 기술을 사용하여 텍스처 매핑된 다각형의 래스터 스캔 동안 UV 좌표를 계산하는 것이 가능하다.^[4] 일부 PC 게임에서 볼 수 있는 복셀 높이맵 소프트웨어 렌더링 엔진도 이 원리를 사용했다.

브레젠험은 또한 실행 슬라이스 계산 알고리즘을 발표했다. 위에 설명된 실행 길이 알고리즘이 주축에서 루프를 실행하는 동안, 실행 슬라이스 변형은 다른 방식으로 루프를 실행한다.^[5] 이 방법은 여러 미국 특허로 대표되었다.

• US patent 5815163, "Method and apparatus to draw line slices during calculation" 
• US patent 5740345, "Method and apparatus for displaying computer graphics data stored in a compressed format with an efficient color indexing system" 
• US patent 5657435, "Run slice line draw engine with non-linear scaling capabilities" 
• US patent 5627957, "Run slice line draw engine with enhanced processing capabilities" 
• US patent 5627956, "Run slice line draw engine with stretching capabilities" 
• US patent 5617524, "Run slice line draw engine with shading capabilities" 
• US patent 5611029, "Run slice line draw engine with non-linear shading capabilities" 
• US patent 5604852, "Method and apparatus for displaying a parametric curve on a video display" 
• US patent 5600769, "Run slice line draw engine with enhanced clipping techniques" 

이 알고리즘은 다음으로 확장되었다.

• 임의 두께의 선 그리기: IBM의 Alan Murphy가 만든 알고리즘.^[6]
• 다양한 종류의 곡선(원, 타원, 3차, 2차, 유리 베지에 곡선) 및 안티앨리어싱 처리된 선과 곡선 그리기: Alois Zingl이 만든 일련의 알고리즘.^[3]

• 디지털 미분 분석기 (그래픽스 알고리즘), 선과 삼각형을 래스터화하는 간단하고 일반적인 방법
• 샤오린 우의 선 알고리즘, 안티앨리어싱으로 선을 그리는 비슷한 빠른 방법
• 중점 원 알고리즘, 원을 그리는 유사 알고리즘

• Bresenham, J. E. (1965). 《Algorithm for computer control of a digital plotter》 (PDF). 《IBM Systems Journal》 4. 25–30쪽. doi:10.1147/sj.41.0025. 2008년 5월 28일에 원본 문서 (PDF)에서 보존된 문서. 
• "The Bresenham Line-Drawing Algorithm", by Colin Flanagan
• Abrash, Michael (1997). 《Michael Abrash's graphics programming black book》. Albany, NY: Coriolis. 654–678쪽. ISBN 978-1-57610-174-2.  게임에서 사용하기 위한 C 및 어셈블리로 작성된 알고리즘의 매우 최적화된 버전과 내부 작동 방식에 대한 완전한 세부 정보 포함
• Zingl, Alois (2016). “A Rasterizing Algorithm for Drawing Curves” (PDF).  지원되지 않는 변수 무시됨: |orig-date= (도움말), The Beauty of Bresenham's Algorithms

• Patrick-Gillesbanda 논문, 3D 은선 제거를 수행하기 위한 브레젠험 직선 그리기 알고리즘의 확장 포함
  • MICAD '87 CAD/CAM 및 컴퓨터 그래픽스 회의록, 591페이지 - ISBN 2-86601-084-1.
• 브레젠험 알고리즘 수정을 통한 선 굵기화, A.S. Murphy, IBM Technical Disclosure Bulletin, Vol. 20, No. 12, May 1978.
• Bresenham, Jack (February 1977). 《A linear algorithm for incremental digital display of circular arcs》. 《Communications of the ACM》 20. 100–106쪽. doi:10.1145/359423.359432.  – 또한 Technical Report 1964 Jan-27 -11- Circle Algorithm TR-02-286 IBM San Jose Lab

위키미디어 공용에 브레젠험 직선 알고리즘 주제와 관련된 미디어 분류가 있습니다.

• Michael Abrash's Graphics Programming Black Book Special Edition: Chapter 35: Bresenham Is Fast, and Fast Is Good
• The Bresenham Line-Drawing Algorithm by Colin Flanagan
• 브레젠험 알고리즘에 대한 미국 국립표준기술연구소 페이지
• Calcomp 563 증분 플로터 정보
• 여러 프로그래밍 언어로 된 브레젠험 알고리즘
• 브레젠험 알고리즘의 아름다움 — 선, 원, 타원 및 베지에 곡선을 그리는 간단한 구현