ワイルズによるフェルマーの最終定理の証明


ワイルズによるフェルマーの最終定理の証明(ワイルズによるフェルマーのさいしゅうていりのしょうめい)は、イギリスの数学者であるアンドリュー・ワイルズによる楕円曲線に関するモジュラリティ定理の特殊な場合の数学的証明である。リベットの定理と組み合わせることでフェルマーの最終定理の証明を与える。フェルマーの最終定理とモジュラリティ定理は双方ともに当時の知識だけで証明することは現実的にほぼ不可能だと考えられており、同時代の数学者の多くは証明することは難しいと考えていた。
ワイルズは1993年6月23日、「モジュラー形式、楕円曲線およびガロワ表現(Modular Forms, Elliptic Curves and Galois Representations.)[1]」と題されたケンブリッジ大学の彼の講演にて最初に証明を発表した。しかし、1993年9月、この証明に誤りが含まれていることが判明した。1年後、1994年9月19日、ワイルズが 「(自身の)今までの職務においてもっとも重要な瞬間」と呼ぶアイデアを得た。彼はこれに関して「信じられないほど美しく…とてもシンプルでかつエレガント」なアイデアと語っており、これによって証明を数学者のコミュニティが受容する水準にまで正すことができた。この正しい証明は1995年に発表された[2]。
ワイルズの証明は代数幾何学・数論のテクニックを多数使用しており、これらの数学分野の派生を多く含んでいる。また、彼の証明はスキームの圏や岩澤理論などのフェルマーが知りえなかった20世紀以降のテクニックを含む現代代数幾何学の一般的な構成を使用している。
証明を含む2本の論文は129ページの長さであり[3][4]、証明を構成するのにワイルズは7年を費やした。ジョン・コーツはアンドリュー・ワイルズの証明を数論の最高の成果の1つであると述べ、ジョン・ホートン・コンウェイはワイルズの証明は20世紀を代表する証明だと述べた[5]。ワイルズのフェルマーの最終定理証明への戦略は、半安定楕円曲線の特殊な場合に関するモジュラリティ定理を証明することであり、強力なモジュラリティのリフトというテクニックを確立し、他の数々の問題に対しても全く新しいアプローチの道を開いた。フェルマーの最終定理の解決に対して、ワイルズはナイトの称号を与えられたほか、2016年のアーベル賞等の名誉が与えられた。ワイルズがアーベル賞を受賞することが発表されたとき、en:Norwegian Academy of Science and Lettersはワイルズの業績を「素晴らしい証明("Stunning proof")」と表現した[2]。
背景[編集]
フェルマーの最終定理[編集]
1637年に書き表されたフェルマーの最終定理は以下を満たす3つの自然数 a, b, c が存在しないことを述べている。
ただし n は 3 以上の自然数である。
ワイルズ以前の特定の指数に関する部分的な解[編集]
フェルマーの最終定理の発表からワイルズの最終的解決まで350年以上が経っており、多数の数学者・アマチュアが n > 2 の場合および特定の指数に限定された場合の双方でフェルマーの定理を証明しようと試みた。およそ400万までの n に関しては、当初は手計算、のちにコンピューターによって正しいことが確認された。しかし一般的な証明はおろかそのような証明に至るヒントすら見つからなかった。
志村・谷山予想[編集]
当時フェルマーの最終定理とは関連しないと考えられていた議論にて、1950-60年代の日本の数学者である志村五郎が同じく日本の谷山豊から着想を得て、当時研究されていた最先端の数学的概念である楕円曲線とモジュラー形式が(両者は全く異なる概念であると考えられていたにも関わらず)互いにつながりを持っている可能性があるという予想を唱えた。
谷山と志村が提出したこの予想はこれら2つの数学的概念が実際は数学的に同じものであり、見方が異なるだけであるというものであった。谷山と志村の予想は「すべての有理数体上に定義された楕円曲線はモジュラーであろう」ということを述べており、後に谷山・志村予想として知られるようになった。西洋においてはこの予想がアンドレ・ヴェイユの1967年の論文によって広く知られるようになったため、しばしば谷山・志村・ヴェイユ予想と呼ばれている。
1980年頃までには楕円曲線の予想を構成するための多くのエビデンスが積み上げられていた。これらの予想は広く真であると考えられていたが何らかの確たる証拠があったわけではなく、(これらの予想が真ならば)理論的に素晴らしく首尾一貫したものであり、なおかつ魅力的な数学的概念を提示するがために広く真であると信じられていた。予想の一部は間違っている可能性もあった。
当時、谷山・志村予想には証明が存在せず、証明に至るアプローチを見つけることすら絶望視されていた。このような背景もあり、証明あるいはそれに至るアプローチの発見すら絶望視されたまま谷山・志村予想は数学上の重要な未解決問題として数十年残り続けた。
谷山・志村によってはじめて予想が発表されてからおよそ50年後、ワイルズの研究の成果により状況が大きく進展してようやく証明され、この予想は現在モジュラリティ定理として知られている。
フライ曲線[編集]
上記の議論とは独立 に、1960年代後半、Yves Hellegouarchがフェルマー予想の解(a,b,c)を全く別の数学的概念である楕円曲線と関連付けることを思いついた[6]。この曲線は(x,y)座標平面上の以下の関係を満たすすべての点によって構成されている。
このような楕円曲線は特殊な性質をもっている。これは等式の数に高次の指数が出現するためであり、また an + bn = cnもまたn次の指数であるためである。
1982-1985年において、ゲルハルト・フライはHellegouarchの曲線の特殊な性質に着目し、これは現在フライ曲線と呼ばれている。フライ曲線はモジュラーでない楕円曲線がフェルマーの最終定理に対する反例を与えることになるというアイディアを提示することでフェルマーの最終定理と谷山・志村予想の橋渡しとなった。
より平易な言葉で言えば、フライの研究はフェルマーの最終定理を否定するような数の組(a,b,c,n)は、谷山・志村予想を否定することも可能であろうと考えるに足るような理由を与えた。よって、もし谷山・志村予想が真であれば、フェルマーの最終定理を否定するような数の組も存在しないであろう。よってフェルマーの最終定理もまた真であろうと考えられる。
- (数学的にはこの予想は有理数の係数を持つ楕円曲線は、単に等式を与えるだけでなく、モジュラー関数を用いる方式で x y 座標上にパラメトリック方程式として構成することも可能ということを述べている。つまりこの予想はQ上のすべての楕円曲線はモジュラー楕円曲線でなければならないということを言っており、フェルマーの最終定理にゼロでない2より大きい a, b, c, n が存在する場合はこれがモジュラーでない楕円曲線に対応するため、矛盾となる)
そのため、谷山・志村予想を証明・反証した場合はフェルマーの最終定理もまた同時に証明・反証されることになる[7]。
1985年にはジャン・ピエール・セールがフライ曲線がモジュラーでないことを部分的に証明した。セールは完全な証明を与えなかったので、証明に欠けていた部分はイプシロン予想として知られるようになった。これは現在、リベットの定理として知られている。セールの主な関心は(谷山・志村予想を暗示する)モジュラーガロワ表現上のセール予想というもっと野心的な予想にあった。セールの証明は完璧ではなかったものの、半安定状態の楕円曲線とフェルマーの最終定理のつながりをほぼ確実なものとするに至った。
フライ曲線を用いたフェルマーの最終定理への挑戦[編集]
上記の戦略に従えばフェルマーの最終定理を証明するには2つのステップを踏む必要がある。1つはセールの部分的な証明を拡張し、フライの直感が正しいことを示すこと。つまり、上記の楕円曲線(フライ曲線)がもし存在するのであれば、それがモジュラーではないことを示すことである。証明の完全でない、欠けていた部分(イプシロン予想)はジャン・ピエール・セールによるものである[8]:1。2つ目は谷山・志村予想を証明することである。あるいは完全に証明せずとも、少なくともフライ曲線を含む楕円曲線(半安定楕円曲線)に関して谷山・志村予想を証明することである。
- もしイプシロン予想が真であれば、フェルマーの最終定理の反例となる a, b, c, n はモジュラーでない半安定楕円曲線(フライ曲線)を構成することができる。
- しかし、もし谷山・志村予想がフライ曲線に関して真であれば、定義からあらゆる(非存在ではない)フライ曲線はモジュラーでなければならない。
- ここから次の結論が導かれる。つまり、もしイプシロン予想および谷山・志村予想がともに真であると証明されれば、それはフェルマー方程式に解が存在しないことを意味する。これは、もしフライ曲線が全く存在しないのであれば両者が互いに矛盾しないためである。このようにフェルマーの最終定理が証明される。
リベットの定理[編集]
1986年夏、ケン・リベットはイプシロン予想を証明することに成功し、これはリベットの定理として知られるようになった。リベットの論文は1990年に発表された。リベットはこの証明を遂げたことで、同時にフェルマーの最終定理とリベットの定理の関係性をも証明した。つまり、フライが示唆したように、半安定楕円曲線に対して谷山・志村予想を証明することは、リベットの定理と組み合わせることで、フェルマーの最終定理を証明することになることが確定したのだった。
数学的な言い方をすれば、リベットの定理は楕円曲線に関連付けられたガロワ表現が(フライ曲線が持つ)ある種の性質を持つならば、その楕円曲線はモジュラーでないことを示し、そのようなガロワ表現を生じさせるようなモジュラー形式もまた存在しないことを示した[9]。
しかしながら、このようなセールとリベットによる研究の進展とは裏腹に、上記で述べられたフェルマーの最終定理へのアプローチは広く現実的には適用不可だと考えられていた。これは谷山・志村予想が当時知られていた知識だけでは全く証明できそうにないと見られていたためである[10]:203–205, 223, 226。例えば、ワイルズのかつての指導者であるジョン・コーツは「(谷山・志村予想は)全く証明できそうにない」[10]:226と述べたし、ケン・リベットは「(自分自身も)証明ができないだろうと考えていた大勢のうちの1人」であるとしていた[10]:223。
アンドリュー・ワイルズ[編集]
リベットの1986年のイプシロン予想の証明を聞き、フェルマーの最終定理に子供のころから魅了されていた、楕円曲線を研究していたイギリスの数学者アンドリュー・ワイルズは、谷山・志村予想の証明を秘密裏に進めることを決めた。これはワイルズの専門分野と(フェルマーの最終定理に)関わりがあることが判明した[11]ためでもあるし、長年未解決だった問題を証明することが彼にとって魅力的だったためでもある。
リベットは後に「ワイルズはおそらくこの地球上で(あの難問に)実際に挑戦して証明できるだなんて夢見るような向こう見ずさを持つ数少ない者のひとりだった」と述べている[10]:223。
証明の発表とその後の発展[編集]
ワイルズは証明を1993年に初めて発表した。これは元々の論文の一箇所に見られた間違いを訂正し、1995年に最終的に正しいものとして受け入れられた。ワイルズの仕事は正しいとされてから、その後の6年で他の数学者によってモジュラリティ定理の完全な証明にまで拡張された。
証明の発表と最終的な証明 (1993–1995)[編集]
19を発表した。この発表はイギリス、ケンブリッジのアイザック・ニュートン数学研究所で3つの講義に渡って行われた[1]。講義の後には比較的大きな規模の記者会見が行われた[12]。
証明の発表の後、ニック・カッツがワイルズの論文の査読を行うレフェリーの一人として指名された。カッツはレビューにおいて、ワイルズに証明に関する様々な質問をしたが、そのうちにワイルズ自身も認めるギャップが証明に含まれることがわかった。証明の重要な箇所(ある種の群の位数に上限を与える部分)の誤りであり、コリヴァキアン=フラッハ法を拡張するのに使用したオイラー系が不完全だったというものだった。
ただし、この誤りによってワイルズの仕事が全く役に立たないものになったわけではなかった。ワイルズの証明のそれぞれの部分は単体でも意義深く革新的なものであり、証明の過程で多くの発展や新たなテクニックが見出されていたためである。この誤りに影響されたのは一箇所のみであった[10]:289, 296–297。しかしながら、この一箇所が(誤りによって)証明されないのであれば、フェルマーの最終定理の証明も成されない。
ワイルズはギャップを取り除くのにほとんど1年を費やした。当初は自身で訂正を試みたが、のちにかつての指導学生のリチャード・テイラーと共同で訂正を試みた。しかし、ギャップを取り除くことはできなかった[13][14][15]。1993年の終わりまでに、厳しい視線が注がれるなかでワイルズの証明が失敗したという噂が広がったが、どの程度深刻なのかに関しては知られていなかった。数学者はワイルズに彼の仕事が完全なのかそうでないのかに関わらず彼の証明を公開させるようにプレッシャーをかけ始めた。そうすることでより広い数学者のコミュニティがワイルズの仕事を精査し、利用することができるからである。しかし、誤りが訂正されるどころか、当初はそれほど深刻でないように思われたギャップは実は非常に重要で、取り除くのは容易でないように思われた[16]。
ワイルズによれば、1994年9月19日の朝、彼はほとんど誤りの訂正を諦める寸前で、証明に失敗したことを認める瀬戸際におり、他の数学者が証明を発展させ、誤りを探すことができるように証明の詳細を発表しようとしていた。彼は証明がなぜ不完全だったのかを理解するための最後の確認をしていたが、不意に、コリヴァキアン=フラッハ法の適用の際に問題となっている部分そのものが(コリヴァキアン=フラッハ法のアプローチから得た経験を援用することで)岩澤理論の適用を可能にすることに気がついた。それぞれのアプローチは単体では不適切だが、両者のアプローチを組み合わせ、双方のアプローチのツールを使用することでギャップを取り除き、(ワイルズが最初に出した論文では証明が与えられていなかった)すべての場合に有効な類数公式(Class Number Formula, CNF)を与えた。[13][17][13]。
- "私はデスクに座ってコリヴァキアン=フラッハ法の確認をしていました。これは私が誤りを訂正できると考えていたからではなく、少なくともなぜこのアプローチが失敗したのか、その理由を説明できるようにしておきたいと考えたからです。すると、突然すばらしいひらめきが頭に浮かびました。コリヴァキアン=フラッハ法のアプローチは駄目でしたが、そうなっている理由がまさに3年前の岩澤理論のアプローチを適用するのに必要なものだったのです。コリヴァキアン=フラッハ法のアプローチの灰から問題に対する真の解答が得られたようでした。それは信じられないほど美しく、シンプルでエレガントでした。なぜそんなことを私が見逃していたのかわかりませんが、その箇所を半信半疑で20分見つめました。それからその日は一日中、部屋の周りを歩き回り、そしてデスクに戻ってその箇所がまだそこにあることを確認するということを繰り返しました。それはそこにありました。私は気持ちを抑えることができませんでした。とても興奮していました。私の職務のうちで、最も重要な瞬間でした。今後、あれほどのことが起こることはないでしょう。"
- — アンドリュー・ワイルズ。サイモン・シンによる引用。[18]
1994年10月6日に、ワイルズは3人の同僚(ゲルト・ファルティングスを含む)に彼の新しい証明を査読するように頼んだ[19][20]。1994年10月24日にワイルズは2つの論文を投稿した。「モジュラー形式、楕円曲線およびガロワ表現(Modular Forms, Elliptic Curves and Galois Representations.)」[3]と「ある種のヘッケ環の環論的性質(Ring theoretic properties of certain Hecke algebras)」[4]である。このうち後者の論文がワイルズがテイラーと共著したものであり、主論文で訂正が必要だった箇所を直し、必要な条件が満たされていることを証明したものである。
この2つの論文は精査され、最終的に1995年5月にAnnals of Mathematicsで発表された。この新しい証明は広く検査され、主な部分に関して正しいものであると受け入れられた[5][9][11]。これらの論文は半安定楕円曲線に関するモジュラリティ定理を確立するものであり、遂にフェルマーの最終定理を証明するものであった。これは予想が提出されてから358年後のことであった。
その後の発展[編集]
フェルマーは「(フェルマーの最終定理に対して)真に驚くべき証明を見つけたが、それを書くにはこの余白は小さすぎる」[21][22]と述べた。 しかし、ワイルズの証明は非常に複雑なものであり、他の数学者の多くの仕事を援用したものであったため、1999年当時ワイルズの証明の全容を詳細まで理解しているのはほんの数人の数学者だけであると示唆されていた[1][23]。ワイルズの証明の複雑さは知られていたので、例えばその理解のために10日間に渡るカンファレンスがボストン大学で開かれた。このカンファレンスの議事録をもとに出版された本は、証明を理解するために必要な前提となる全範囲のトピックを数論の大学院生を対象に説明することを目的としている[8]。
上記で記されたように、ワイルズは谷山・志村予想を半安定楕円曲線の特別な場合に関してのみ証明したので、すべての楕円曲線に関して証明されたわけではなかった。しかし、ワイルズの証明から数年して、クリストフ・ブルイユ、ブライアン・コンラッド、フレッド・ダイアモンド、リチャード・テイラー(しばしば「BCDT」と略される)の4人がワイルズの仕事を発展させ、最終的に2001年の論文で谷山・志村予想をすべての楕円曲線に関して証明した[24]。証明されたあとは、谷山・志村予想はモジュラリティ定理として知られている。
2005年にオランダの計算機科学者Jan Bergstraはワイルズの証明をコンピューターで真偽の判定をできるような形にする場合の問題点を発表した[25]。
ワイルズの証明の概要[編集]
ワイルズは半安定楕円曲線に関してモジュラリティ定理を証明し、そこからフェルマーの最終定理が背理法で導かれることを明らかにした。
証明は大きく2つの部分に分かれる。まずワイルズは「保型性持ち上げ定理(英: modularity lifting theorem)」 として知られるリフトに関する一般的な結果を証明する。これにより、楕円曲線に関する問題を、それらのガロア表現に関する問題に変換して証明することができる。後半では、全ての半安定曲線がモジュラーであることの証明を、それらのガロア表現がモジュラーであることを証明する形で行う。
| 証明の概要 | コメント | |
|---|---|---|
| 第1部:証明の準備 | ||
| 1 | 証明は背理法による。まずフェルマーの最終定理を偽と仮定し、an + bn = cn を満たす 0 でない解(有理数 a, b, c と素数 n ≥ 3)が存在するとする。 | |
| 2 | a, b, c, n を用いて半安定楕円曲線 E を作ることができるが、リベットの定理より E はモジュラーとはならない。 | もし、そのような楕円曲線が全てモジュラーになることを証明できれば、矛盾が生じ仮定(a, b, c, n が存在すること)が否定され、フェルマーの最終定理が真であると証明される。 |
| 3 | フェルマーの最終定理が偽、即ちフェルマー方程式の解 a, b, c, n が存在すると仮定し、その解から半安定楕円曲線であるフライ曲線を作る。この曲線を E とおき、矛盾を導く。 | |
| 第2部:保型性持ち上げ定理 | ||
| 4 | 任意の素数 p > 3 に対する楕円曲線 ρ(E, p) のガロア表現は、多くの数学者によって研究されている。 ワイルズはまず、これらの表現について「半安定楕円曲線 E がモジュラーなガロア表現 ρ(E, p) を持つならば、E 自体もモジュラーである」という定理の証明を目指す。 この定理には二つの利点がある。まず、数え方やマッチングが簡単になる点。そして、この素数 p は自由に選んでよいという点である。 この証明はこの問題の最も難しい部分で、より厳密には「ガロア表現 ρ(E, p) がモジュラー形式であれば、他の全ての関連するガロア表現 ρ(E, p∞)( p の全ての冪)もモジュラー形式である」という証明をすることになる。[2]これはいわゆる「保型性持ち上げ問題」であり、ワイルズは変形を使ってこれに取り組んだ。 楕円曲線(または楕円曲線の表現)は、可約または既約のいずれかに分類できる。楕円曲線の表現が可約かどうかで、証明の仕方が少し違ってくる。 | 楕円曲線とモジュラー形式を直接比較することは難しく、過去に楕円曲線とモジュラー形式を数え上げ、マッチングさせる試みはすべて失敗している。しかし、楕円曲線はガロア理論における表現が可能である。ワイルズは、楕円曲線そのものではなく、それら表現を使って作業すれば、楕円曲線の数え上げとモジュラー形式とのマッチングがはるかに容易になることに気づいた。これ以降、証明は主に以下のことを目指す。
これらの証明により(楕円曲線そのものを直接扱う代わりにそれらの表現を扱えるようになるので)目指す目標は、半安定楕円曲線の幾何学的ガロア表現のモジュラリティを証明することへと変わる。ワイルズはこの実現を "key breakthrough" と表現している。 楕円曲線のガロア表現は G → GL(Zp) である。楕円曲線の幾何学的ガロア表現がモジュラー形式であることを示すには、正規化固有形式であってその固有値(そのフーリエ級数の係数でもある)が有限個の素数を除くすべての素数に対して合同関係を満たすものを見つける必要がある。 |
| 5 | ワイルズの最初の戦略は、帰納法と類数公式を用いた数え上げとマッチングである。 | ワイルズはこの分野で、最初は horizontal Iwasawa theory で、後にはコリヴァギン・フラッハ法の拡張で困難に直面することになった。ワイルズのコリヴァギン・フラッハ法の拡張は、主に、彼が使う完全な類数公式を証明するためにコリヴァギン・フラッハ法を十分に強くすることに関連していた。その後、どちらのアプローチも単独では半安定楕円曲線の全種類をカバーできる類数公式を生成できないことが判明し、1995 年の彼の証明の最後のピースは、コリヴァギン・フラッハ法の技術で岩澤理論を強化すれば成功することを理解したことだった。 |
| 6 | この時点で、ガロア表現に関する重要なポイントが証明されたことになる。
これがワイルズの保型性持ち上げ定理であり、当時としては画期的な大成果であった。 | これの嬉しい所は、自由に素数 p > 2 を選んで証明すれば全ての素数 > 2 について言えたことになる所である。 これにより一つの素数 p を用いて全ての楕円曲線がモジュラーであることを証明できる可能性が出てきた。もし仮に一つで上手く行かなかったとしても、その時々に応じて p を変えてやれば上手くいく可能性が残されている。 証明は全ての半安定楕円曲線 E のガロア表現を対象としなければならないが、個々の曲線については、一つの素数 p を用いてモジュラーであることを証明すればよい。 |
| 第3部:全ての半安定楕円曲線がモジュラーであることの証明 | ||
| 7 | 保型性持ち上げ定理が証明されたので、元の問題に戻ろう。半安定楕円曲線をガロア表現の可約性に基づいて分類し、その結果に保型性持ち上げ定理を適用する。 既に述べたように、表現にはどの素数を用いてもよいので、今回は最も簡単になる素数を選ぶことにする。3 は(2 より大きい)最小の素数であり、ρ(E, 3) を使った楕円曲線の表現については既に研究が存在するので、素数として 3 を選ぶことは出発点として有用であろう。 ワイルズは、表現 ρ(E, 3) が既約である場合は素数 p = 3 を選び、ρ(E, 3) が可約である場合は p = 5 を選ぶ方が(それがモジュラーであることの)証明が簡単になることを発見した。つまり、この時点で証明は二つに分かれる。 | この証明のように p = 3 と p = 5 の二つを用いる手法は "3/5 switch" と呼ばれるもので、1993 年に Mazur の論文でワイルズが注目した手法だが、それ自体は 19 世紀までさかのぼることができる。 p = 3 と p = 5 の切り替えは、その後それ自体で重要な研究領域を開いた(セールの保型性予想を参照)。 |
| 8 | まず ρ(E, 3) が既約な場合を考える。 この場合 ρ(E, 3) が常にモジュラーとなることは 1980 年頃から知られていた。そのため保型性持ち上げ定理から E がモジュラーとなることが直ちに従う。 | 1980 年代初頭にラングランズとタネルが 2 つの論文で証明している。この証明は ρ(E, 3) が 1 変数の一般的な4次方程式と同じ対称群を持っていることに基づいており、当時モジュラーであることが知られていた数少ない一般クラスのディオファントス方程式の一つであった。 この p = 3 の既存の結果はワイルズのアプローチにとって重要であり、最初に p = 3 を用いた理由の1つである。 |
| 9 | 次に ρ(E, 3) が可約な場合を考える。 ワイルズは ρ(E, 3) が可約な場合、代わりに ρ(E, 5) に保型性持ち上げ定理を適用する方が(常にモジュラーであることの)証明が簡単になることを発見した。 | 既約でないので保型性持ち上げ定理は適用できない。そこで今度は一つ大きい素数 p = 5 を用いて攻めてみることにする。しかし ρ(E, 5) が常にモジュラーであることを証明するのは、そのままでは絶望的に見える。これは一般的な五次方程式が冪根によって解けないのと同じ理由である。そこでワイルズは上手い方法を見つける必要があった。 |
| 9.1 | ρ(E, 3) と ρ(E, 5) がともに可約ならば、ρ(E, 5) は常にモジュラーとなることをワイルズは直接証明した。 | |
| 9.2 | 最後のケースは ρ(E, 3) が可約かつ ρ(E, 5) が既約な場合である。 この場合、ρ(F, 3) が既約で、かつ ρ(E, 5) と ρ(F, 5) が同型表現である別の半可換楕円曲線 F が常に見つけられることがワイルズによって示されている。
| |
| 9.3 | 従って、ρ(E, 3) が可約であれば、ρ(E, 5) は常にモジュラーであることが証明された。 | このステップでは、保型性持ち上げ定理の真価が発揮される。 |
| 結論 | ||
| 10 | これで ρ(E, 3) が既約であろうとなかろうと、E(半安定楕円曲線であれば何でもよい)は常にモジュラーであることが証明された。このことは、全ての半安定楕円曲線はモジュラーであることを意味する。 これは次のことを証明している。
| もしフェルマーの最終定理が偽ならば、モジュラーであり(ワイルズによる結果)かつモジュラーでない(リベットの定理)半安定楕円曲線を作れることを証明したので、背理法により真であることが証明された。両方にはなりえないので、そのような曲線は存在しないというのが唯一の答えである。 |
ワイルズの証明の数学的詳細[編集]
この節は英語から大ざっぱに翻訳されたものであり、場合によっては不慣れな翻訳者や機械翻訳によって翻訳されたものかもしれません。 |
概要[編集]
ワイルズは楕円曲線をモジュラー形式の可算集合にマッチングさせることを試みた.彼はこの直接的なアプローチがうまくいかないことを発見し、代わりに楕円曲線のガロア表現をモジュラー形式にマッチングさせることで問題を変換した。ワイルズはこのマッチング(または写像)を、より具体的には環準同型と表現している。
は変形環であり、はHecke ring(局所的にコンパクトな群のヘッケ代数)である。
ワイルズは多くの場合、この環の準同型が環の同型になりうるという洞察を得た(1995年の論文の第2章§3の予想2.16[3])。彼はと間の写像が、理論に現れる二つのアーベル群が有限で同じ濃度を持っている場合にのみ同型性であることに気がついた。これは「数的基準」と呼ばれることもある。この結果、フェルマーの最終定理は、2つの群が同じ位数を持つという記述に還元される。この証明の文章の多くは、環論や並べ換え理論に関連する話題や定理へとつながっている。Wilesの目標は、写像 が同型であることを検証し、最終的に とすることであった。変形を扱う際、ワイルズは4つのケースを定義したが、平坦の変形ケースは証明に手間がかかり、同巻の別論文「あるヘッケ代数の環論的性質」で扱われている。
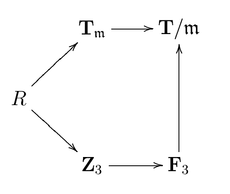
ゲルト・ファルティングスは、その会報で次の可換図式を与えている(p. 745)。
あるいは究極的には となり、完全交差であることが示される。ワイルズは を直接示せなかったので、 と による lifts でそれを実現した。
このマッチングを行うために、ワイルズは類数公式(CNF)を作成する必要があった。当初、水平方向の岩澤理論を使おうとしたが、その部分には未解決の問題があり、CNFを作成することはできなかった。1991年の夏の終わりに、ヴィクター・コリヴァギンとマティアス・フラッハが開発した、証明の誘導部分に「ぴったり」であり、CNFを作成するために使用できるようなオイラー系 について知り、ワイルズは彼の証明が必要とするCNFを作成するために、岩澤研究を置いて、Kolyvaginとフラッハの仕事を拡張し始めることにした。 [26]1993年の春までに、研究は楕円曲線のいくつかの族を除いてすべてカバーしており、1993年の初めには、ワイルズは成功が近いことを確信して、信頼できる同僚に秘密を打ち明けた。彼の研究はコリヴァギン–フラッハのアプローチに大きく依存しており、それは数学にとってもワイルズにとっても新しいものであり、ワイルズ自身それを拡張していたので、1993年1月にはプリンストン大学の同僚ニック・カッツに、研究に微妙な間違いがないか見直すのを手伝ってくれよう依頼した。当時の彼らの結論は、ワイルズが使った技法は正しく機能しているようだというものだった。[10]:261-265[27].
コリヴァギン–フラッハ法の使用は、後に元の証明提出における失敗のポイントであることが判明し、結局彼は岩沢理論とリチャード・テイラーとの共同作業に戻して修正しなければならなくなった。1993年5月、Mazurの論文を読んでいたWilesは、3/5スイッチで最後の問題が解決し、その後すべての楕円曲線をカバーできることを洞察した。
一般的なアプローチと戦略[編集]
有理数の体Q 上の楕円曲線 Eが与えられたとき、すべての素数乗 に対して、絶対ガロア群
から
の 準同型が存在する。 は、の法を整数とする2×2行列のinvertible群である。
これは, 即ち 上のEの点は アーベル群をなし、その上には が作用しているからである: なるxのなす部分群は , であり、この群の automorphism は既に説明したタイプの行列である。
これはアイヒラーや志村にさかのぼる。 ガロア群は、まずモジュラー形式が定義されたモジュラー曲線に作用し、次にその曲線のヤコビアン・バラエティに作用し、最後にそのヤコビアンの乗次点に作用する。 結果として得られる表現は通常2次元ではないが、Hecke operatorが2次元の部分を切り出している。 これらの表現がある楕円曲線に由来することを証明するのは簡単だが、その逆を証明するのは難しい。
楕円曲線から直接モジュラー形式へ行こうとするのではなく、あるℓとnに対して 表現へ行き、そこからモジュラー形式へ行けば良い。 ℓ = 3 and n= 1の場合、 Langlands-Tunnell theorem の結果、 Q 上の任意の楕円曲線の representation は、あるモジュラー形式から来ることがわかる。 基本的な戦略は、ℓ = 3 と任意の n に対してこれが正しいこと、つまりすべての n に対して有効な単一のモジュラー形式が存在することを n の帰納法を用いて示すことである。 そのためには、 をlift できる方法の数を比較する、計数論的な議論を用いる。\のGalois表現を にできる数と、 モジュラー形式を持ち上げられる数とを比較する。
重要な点は、ガロア表現に十分な条件を課すことである。さもなければ、リフトが多すぎて、ほとんどがモジュラー形式にはならない。 この条件は、モジュラー形式から来る表現と楕円曲線から来る表現で満たされる必要がある。
3-5トリック[編集]
この場合、最後のトリックがある。これはその後のSerre予想 (整数論)の研究でより一般的に研究されるようになった。これはと表現の間の相互作用に関わるアイデアである。特に、Q 上の半安定楕円曲線 E に関連する mod-5 Galois 表現 が既約であるならば、その関連 mod-5 Galois 表現 が に同型であり、その関連する mod-3 Galois 表現 が既約(したがって Langlands-Tunnell によるモジュール)であるようなものを超える E' である。[28]
Wilesの証明の構成[編集]
Wilesの証明の構成は以下の通り。 1995年に発表された108ページの論文で、ワイルズは主題を以下の章に分割している(ここではページ番号で先行)。
その後、ゲルト・ファルティングスは1995年の証明にいくつかの簡略化を施し、主に幾何学的な構成からより単純な代数的なものに切り替えた。 [19][29] コーネル会議の本には、元の証明に対する簡略化も含まれていた。
文献の概要[編集]
ワイルズの論文は100ページを超えるもので、群論、代数幾何、可換環論、ガロア理論の専門的な記号や表記がよく使われている。ワイルズの基礎作りに貢献した数学者たちは、しばしば新しい専門的な概念や技術的な専門用語を生み出している。
紹介されたものの中には、Ribetが1993年に送ったメールもある;[30][31] Hesselinkのトップレベルの問題のクイックレビューでは、初等代数だけを与え、抽象代数を避けている;[25]あるいは、DaneyのWebページでは、彼自身のノートとこのテーマで入手できる最新の書籍のリストを提供している。Westonは科目間の関係のいくつかの便利な地図を提供しようと試みている。[32] F. Q. Gouvêaの必修項目のいくつかを見直した、1994年の論文「A Marvelous Proof」はLester R. Ford賞を獲得した。[33][34] Faltingsのこの問題に関する5ページの技術速報は、非専門家向けに証明について素早く技術的にレビューしているものです。 [35] 市販のガイド本を探している人には、抽象代数に詳しい人はHellegouarchを読んで、次にコーネルの本[8]は「整数論の大学院生」にも理解できるとされている。コーネル社の本はワイルズの証明の全てを網羅しているわけではない[12]。
脚注[編集]
- ^ a b c Kolata, Gina (1993年6月24日). “At Last, Shout of 'Eureka!' In Age-Old Math Mystery”. The New York Times 2013年1月21日閲覧。
- ^ a b c “The Abel Prize 2016”. Norwegian Academy of Science and Letters (2016年). 2017年6月29日閲覧。
- ^ a b c Wiles, Andrew (1995). “Modular elliptic curves and Fermat's Last Theorem” (PDF). Annals of Mathematics (Annals of Mathematics) 141 (3): 443–551. doi:10.2307/2118559. JSTOR 2118559. OCLC 37032255.
- ^ a b Taylor R, Wiles A (1995). “Ring theoretic properties of certain Hecke algebras”. Annals of Mathematics (Annals of Mathematics) 141 (3): 553–572. doi:10.2307/2118560. JSTOR 2118560. OCLC 37032255. オリジナルの27 November 2001時点におけるアーカイブ。.
- ^ a b “NOVA - Transcripts - The Proof - PBS”. PBS (2006年9月). 2017年6月29日閲覧。
- ^ Hellegouarch, Yves (2001). Invitation to the Mathematics of Fermat–Wiles. Academic Press. ISBN 978-0-12-339251-0
- ^ Singh, pp. 194–198; Aczel, pp. 109–114.
- ^ a b c G. Cornell, J. H. Silverman and G. Stevens, Modular forms and Fermat's Last Theorem, ISBN 0-387-94609-8
- ^ a b Daney, Charles (1996年3月13日). “The Proof of Fermat's Last Theorem”. 2008年12月10日時点のオリジナルよりアーカイブ。2017年6月29日閲覧。
- ^ a b c d e f Fermat's Last Theorem, Simon Singh, 1997, ISBN 1-85702-521-0
- ^ a b “Andrew Wiles on Solving Fermat”. PBS (2000年11月1日). 2017年6月29日閲覧。
- ^ a b Buzzard, Kevin (22 February 1999). “Review of Modular forms and Fermat's Last Theorem, by G. Cornell, J. H. Silverman, and G. Stevens”. Bulletin of the American Mathematical Society 36 (2): 261–266. doi:10.1090/S0273-0979-99-00778-8.
- ^ a b c Singh, pp. 269–277.
- ^ Kolata, Gina (1994年6月28日). “A Year Later, Snag Persists In Math Proof” (英語). The New York Times. ISSN 0362-4331 2017年6月29日閲覧。
- ^ Kolata, Gina (1994年7月3日). “June 26-July 2; A Year Later Fermat's Puzzle Is Still Not Quite Q.E.D.” (英語). The New York Times. ISSN 0362-4331 2017年6月29日閲覧。
- ^ Singh, pp. 175-185.
- ^ Aczel, pp. 132–134.
- ^ Singh p.186-187 (text condensed).
- ^ a b “Fermat's last theorem”. MacTutor History of Mathematics (1996年2月). 2017年6月29日閲覧。
- ^ Malek, Massoud (1996年1月6日). “Fermat's Last Theorem”. 2017年6月29日閲覧。
- ^ Cornell, Gary; Silverman, Joseph H.; Stevens, Glenn (2013). Modular Forms and Fermat's Last Theorem (illustrated ed.). Springer Science & Business Media. p. 549. ISBN 978-1-4612-1974-3 Extract of page 549
- ^ O'Carroll, Eoin (2011年8月17日). “Why Pierre de Fermat is the patron saint of unfinished business”. The Christian Science Monitor. ISSN 0882-7729 2017年6月29日閲覧。
- ^ Granville, Andrew. “History of Fermat's Last Theorem”. 2017年6月29日閲覧。
- ^ Breuil, Christophe; Conrad, Brian; Diamond, Fred; Taylor, Richard (2001). “On the modularity of elliptic curves over 𝐐: Wild 3-adic exercises”. Journal of the American Mathematical Society 14 (4): 843–939. doi:10.1090/S0894-0347-01-00370-8. ISSN 0894-0347.
- ^ a b Hesselink, Wim H. (2008年4月3日). “Computer verification of Wiles' proof of Fermat's Last Theorem”. www.cs.rug.nl. 2017年6月29日閲覧。
- ^ Singh p.259-262
- ^ Singh, pp.239-243; Aczel, pp.122-125.
- ^ Chapter 5 of Wiles, Andrew (1995). “Modular elliptic curves and Fermat's Last Theorem”. Annals of Mathematics 141 (3): 443–551. doi:10.2307/2118559. JSTOR 2118559. OCLC 37032255.
- ^ Malek, Massoud (1996年1月6日). “フェルマーの最終定理”. 2017年6月29日閲覧。
- ^ “sci.math FAQ: Wiles attack”. www.faqs.org. 2017年6月29日閲覧。
- ^ ca/~andrew/PDF/FLTatlast.pdf “Fermat's Last Theorem, a Theorem at Last”. FOCUS. (August 1993) 2017年6月29日閲覧。.
- ^ Weston, Tom. “Research Summary Topics”. people.math.umass.edu. 2017年6月29日閲覧。
- ^ Gouvêa, Fernando (1994). org/programs/maa-awards/writing-awards/a-marvelous-proof “A Marvelous Proof”. American Mathematical Monthly 101 (3): 203–222. doi:10.2307/2975598. JSTOR 2975598 2017年6月29日閲覧。.
- ^ “d.umn.edu/~jgallian/maaawards/ford.html The Mathematical Association of America's Lester R. Ford Award”. 2017年6月29日閲覧。
- ^ Faltings, Gerd (1995年7月). “R. Taylor and A. Fermat's Last Theoremの証明. Wiles”. Notices of the American Mathematical Society 42 (7): 743–746.
参考文献[編集]
- Aczel, Amir (1 January 1997). Fermat's Last Theorem: Unlocking the Secret of an Ancient Mathematical Problem. ISBN 978-1-56858-077-7. Zbl 0878.11003
- John Coates (July 1996). “Wiles Receives NAS Award in Mathematics” (PDF). Notices of the AMS 43 (7): 760–763. Zbl 1029.01513.
- Cornell, Gary (1 January 1998). Modular Forms and Fermat's Last Theorem. ISBN 0-387-94609-8. Zbl 0878.11004 (Cornell, et al.)
- Daney, Charles (2003年). “The Mathematics of Fermat's Last Theorem”. 2004年8月3日時点のオリジナルよりアーカイブ。2004年8月5日閲覧。
- Darmon, H. (2007年9月9日). “Wiles’ theorem and the arithmetic of elliptic curves”. 2018年6月3日閲覧。
- Faltings, Gerd (July 1995). “The Proof of Fermat's Last Theorem by R. Taylor and A. Wiles” (PDF). Notices of the AMS 42 (7): 743–746. ISSN 0002-9920. Zbl 1047.11510.
- Frey, Gerhard (1986). “Links between stable elliptic curves and certain diophantine equations”. Ann. Univ. Sarav. Ser. Math. 1: 1–40. Zbl 0586.10010.
- Hellegouarch, Yves (1 January 2001). Invitation to the Mathematics of Fermat–Wiles. ISBN 0-12-339251-9. Zbl 0887.11003 See review
- “The bluffer's guide to Fermat's Last Theorem”. 2018年6月3日閲覧。 (collected by Lim Lek-Heng)
- Mozzochi, Charles (7 December 2000). The Fermat Diary. American Mathematical Society. ISBN 978-0-8218-2670-6. Zbl 0955.11002 See also Gouvêa, Fernando Q. (2001). “Review: Wiles's Proof, 1993–1995: The Fermat Diary by C. J. Mozzochi”. American Scientist 89 (3): 281–282.
- Mozzochi, Charles (6 July 2006). The Fermat Proof. Trafford Publishing. ISBN 1-4120-2203-7. Zbl 1104.11001
- O'Connor, J. J. (1996年). “Fermat's last theorem”. 2004年8月5日閲覧。
- van der Poorten, Alfred (1 January 1996). Notes on Fermat's Last Theorem. ISBN 0-471-06261-8. Zbl 0882.11001
- Ribenboim, Paulo (1 January 2000). Fermat's Last Theorem for Amateurs. ISBN 0-387-98508-5. Zbl 0920.11016
- Ribet, Ken (1995年). “Galois representations and modular forms” (PDF). 2016年3月17日閲覧。 Discusses various material which is related to the proof of Fermat's Last Theorem: elliptic curves, modular forms, Galois representations and their deformations, Frey's construction, and the conjectures of Serre and of Taniyama–Shimura.
- Singh, Simon (October 1998). Fermat's Enigma. New York: Anchor Books. ISBN 978-0-385-49362-8. Zbl 0930.00002
- Simon Singh “The Whole Story”. 2011年5月10日時点のオリジナルよりアーカイブ。2018年6月3日閲覧。 Edited version of ~2,000-word essay published in Prometheus magazine, describing Andrew Wiles's successful journey.
- Richard Taylor and Andrew Wiles (May 1995). “Ring-theoretic properties of certain Hecke algebras” (PDF). Annals of Mathematics (Annals of Mathematics) 141 (3): 553–572. doi:10.2307/2118560. ISSN 0003-486X. JSTOR 2118560. OCLC 37032255. Zbl 0823.11030.
- Wiles, Andrew (1995). “Modular elliptic curves and Fermat's Last Theorem” (PDF). Annals of Mathematics (Annals of Mathematics) 142 (3): 443–551. doi:10.2307/2118559. ISSN 0003-486X. JSTOR 2118559. OCLC 37032255. Zbl 0823.11029. See also this smaller and searchable PDF text version. (The larger PDF misquotes the volume number as 142.)
外部リンク[編集]
- Weisstein, Eric W. "Fermat's Last Theorem". mathworld.wolfram.com (英語).
- “The Proof”. 2018年6月3日閲覧。 The title of one edition of the PBS television series NOVA discusses Andrew Wiles's effort to prove Fermat's Last Theorem that broadcast on BBC Horizon and UTV/Documentary as Fermat's Last Theorem (Adobe Flash) (
 要購読契約)
要購読契約) - Wiles, Ribet, Shimura–Taniyama–Weil and Fermat's Last Theorem
- Are mathematicians finally satisfied with Andrew Wiles's proof of Fermat's Last Theorem? Why has this theorem been so difficult to prove?, Scientific American, 21 October 1999