Point de Frégier


Le point de Frégier[1] est, en géométrie, un point associé à un point d'une conique (ellipse, parabole ou hyperbole).
Théorème et définition[modifier | modifier le code]

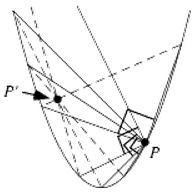
Théorème — Soit une conique et M un point de cette conique. Toutes les cordes de la conique vues sous un angle droit depuis M sont sécantes en un même point F.
Ce point d'intersection est appelé point de Frégier de M[2].
La démonstration donnée par Frégier est purement analytique (calculatoire) :
- il définit un repère orthonormé d'origine M, un des axes étant tangent à la conique ;
- il calcule l'équation de la conique dans ce repère ;
- il en déduit l'équation de cordes vues sous un certain angle depuis M ;
- il en déduit l'existence d'un point F appartenant à toutes ces cordes et donne ses coordonnées[3].
Interprétation[modifier | modifier le code]

Considérons un cercle de centre O, A un point de ce cercle et (d) une droite. L'image du cercle par homologie harmonique de centre A et d'axe (d) est une ellipse tangente au cercle en A (illustration). Les points M et N d'un diamètre du cercle ont pour homologues M' et N' sur l'ellipse. M et N sont vus sous un angle droit depuis A, et de la même façon M' et N' sont vus sous un angle droit depuis A. L'homologue de O est le point de Frégier F de A[4].
Application pratique[modifier | modifier le code]
Le théorème de Frégier fournit un moyen pratique de construire à la règle et à l'équerre la tangente à une conique en un point M quelconque de cette conique :
- on mène par M une droite arbitraire et la droite qui lui est perpendiculaire ;
- ces droites coupent la conique en deux points, que l'on joint : on a obtenu un triangle rectangle en M ;
- on recommence les étapes précédentes avec une autre droite arbitraire ;
- les hypoténuses des deux triangles rectangles ainsi obtenus se coupent en F ;
- la tangente en M à la conique sera la droite perpendiculaire à (MF) passant par M[3].
Propriété[modifier | modifier le code]
Le lieu des points de Frégier d'une conique est en général une conique de type identique, de même centre :
- les points de Frégier d'une parabole sont une parabole déduite de la parabole d'origine par translation
- les points de Frégier d'une hyperbole ou d'une ellipse sont une conique de même centre homothétique à la conique d'origine[4].
Dans le cas d'un cercle, ce lieu est réduit au centre du cercle.
Généralisation[modifier | modifier le code]
Le théorème de Frégier a été établi à l'origine dans le plan (dimension 2), mais il se généralise en dimension n.
Soit M un point d'une quadrique en dimension n. Les repères orthonormés issus de M coupent la quadrique en n points. Ces n points définissent un hyperplan (dimension n - 1), qui passe toujours par un point fixe F, le point de Frégier[5].
Bibliographie[modifier | modifier le code]
- Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009, (ISBN 978-2-91-635208-4)
- Méthodes modernes en géométrie de Jean Fresnel
- Bruno Ingrao, Coniques affines, euclidiennes et projectives, C&M, (ISBN 978-2-916352-12-1)
Notes et références[modifier | modifier le code]
- M. Frégier est un mathématicien français, ancien élève de l'École polytechnique et professeur au Collège de Troyes. Il publia plusieurs articles dans les Annales de Gergonne dans les années 1810. (« Recherche », sur numdam.org).
- (en) Eric W. Weisstein, « Frégier's Theorem », sur MathWorld.
- Frégier, « Géométrie analitique. Théorèmes nouveaux sur les lignes et surfaces du second ordre », Annales de mathématiques pures et appliquées, tome 6, 1815-1816, p. 229-241.
- Michel Guillerault, « Le point de Frégier », Cabri-géomètre,
- Point de Frégier en dimension n, Les Mathématiques.net, 21 décembre 2008.