Courbe de De Rham

Cet article ne cite pas suffisamment ses sources (mai 2024).

Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ».

En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?

En mathématiques, une courbe de De Rham est une courbe fractale continue obtenue comme l'image de l'espace de Cantor ou, de manière équivalente, à partir du développement en base 2 des nombres réels dans l'intervalle unité. De nombreuses courbes fractales bien connues, dont la fonction de Cantor, la courbe de Cesàro-Faber ( courbe C de Lévy ), la fonction point d'interrogation de Minkowski, la courbe de blanc-manger et la courbe de Koch sont toutes des exemples de courbes de De Rham. La forme générale de la courbe a été décrite pour la première fois par Georges de Rham en 1957^[1].

Construction[modifier | modifier le code]

On considère un espace métrique complet ${\displaystyle (M,d)}$ (en général ${\displaystyle \mathbb {R} }$ ² avec la distance euclidienne habituelle), et une paire d'applications contractantes sur M :

${\displaystyle d_{0}:\ M\to M,\ d_{1}:\ M\to M.}$

D'après le théorème du point fixe de Banach, ceux-ci ont des points fixes ${\displaystyle p_{0}}$ et ${\displaystyle p_{1}}$ respectivement. Soit x un nombre réel dans l'intervalle ${\displaystyle [0;1]}$, ayant un développement binaire

${\displaystyle x=\sum _{k=1}^{\infty }{\frac {b_{k}}{2^{k}}},}$

où chaque ${\displaystyle b_{k}}$ vaut 0 ou 1. On considère l'application

${\displaystyle c_{x}:\ M\to M}$

définie par

${\displaystyle c_{x}=d_{b_{1}}\circ d_{b_{2}}\circ \cdots \circ d_{b_{k}}\circ \cdots ,}$

où ${\displaystyle \circ }$ désigne la composition des fonctions. On peut montrer que chaque ${\displaystyle c_{x}}$ projette le bassin d’attraction commun de ${\displaystyle d_{0}}$ et ${\displaystyle d_{1}}$ vers un seul point ${\displaystyle p_{x}}$ dans ${\displaystyle M}$. L'ensemble de points ${\displaystyle p_{x}}$, paramétrée par un seul paramètre réel x, est connue sous le nom de courbe de De Rham.

Condition de continuité[modifier | modifier le code]

La construction en termes de chiffres binaires peut être comprise de deux manières distinctes. Une solution consiste à projeter l'espace de Cantor en des points distincts du plan. L'espace de Cantor est l'ensemble de toutes les chaînes infiniment longues de chiffres binaires. C'est un espace discret et non connexe. L'espace de Cantor peut être projeté sur l'intervalle réel unité en voyant chaque chaîne comme un développement binaire d'un nombre réel. Dans cette carte, les fractions dyadiques ont deux représentations distinctes sous forme de chaînes de chiffres binaires. Par exemple, le nombre réel 1/2 a deux développements binaires équivalents : ${\displaystyle h_{1}=0,1000\cdots }$ et ${\displaystyle h_{0}=0,01111\cdots }$, de manière analogue à l'égalité 0,999... = 1,000... en termes de développements décimaux. Les deux points ${\displaystyle h_{0}}$ et ${\displaystyle h_{1}}$ sont des points distincts dans l'espace de Cantor, mais les deux sont projetés sur le nombre même réel 1/2. Ainsi, les réels de l’intervalle unité sont une image continue de l’espace de Cantor.

La même notion de continuité est appliquée à la courbe de De Rham en demandant que les points fixes soient appariés, de sorte que

${\displaystyle d_{0}(p_{1})=d_{1}(p_{0})}$

Avec cet appariement, les développements binaires des fractions dyadiques correspondent toujours au même point, assurant ainsi la continuité à ce point. On considére le comportement en 1/2. Pour tout point p du plan, on a deux suites distinctes :

${\displaystyle d_{0}\circ d_{1}\circ d_{1}\circ d_{1}\circ \cdots (p)}$

${\displaystyle d_{1}\circ d_{0}\circ d_{0}\circ d_{0}\circ \cdots (p)}$

correspondant aux deux développements binaires ${\displaystyle 1/2=0,01111\cdots }$ et ${\displaystyle 1/2=0,1000\cdots }$. Puisque les deux applications sont toutes deux contractantes, la première suite converge vers ${\displaystyle d_{0}(p_{1})}$ et la deuxième à ${\displaystyle d_{1}(p_{0})}$. Si ces deux éléments sont égaux, alors les deux développements binaires de 1/2 correspondent au même point. Cet argument peut être répété à n’importe quelle fraction dyadique, assurant ainsi la continuité en ces points. Les nombres réels qui ne sont pas des fractions dyadiques n'ont qu'une seule représentation binaire unique, et il s'ensuit que la courbe ne peut pas être discontinue en de tels points. La courbe de De Rham résultante ${\displaystyle p_{x}}$ est une fonction continue de x, pour tout x.

En général, les courbes de De Rham ne sont pas dérivables.

Propriétés[modifier | modifier le code]

Les courbes de De Rham sont par construction auto-similaires, puisque

${\displaystyle p(x)=d_{0}(p(2x))}$ pour ${\displaystyle x\in [0,1/2]}$ et

${\displaystyle p(x)=d_{1}(p(2x-1))}$ pour ${\displaystyle x\in [1/2,1].}$

Les auto-symétries de toutes les courbes de De Rham sont données par le monoïde qui décrit les symétries de l'arbre binaire infini ou espace de Cantor. Ce soi-disant monoïde à doublement de période est un sous-ensemble du groupe modulaire.

L'image de la courbe, c'est à dire l'ensemble des points ${\displaystyle \{p(x),x\in [0;1]\}}$, peut être obtenu par un système de fonctions itérées utilisant l'ensemble des applications contractantes ${\displaystyle \{d_{0},\ d_{1}\}}$. Mais le résultat d’un système de fonctions itérées avec deux applications contractantes est une courbe de De Rham si et seulement si les applications contractantes satisfont à la condition de continuité.

Des exemples détaillés et concrets des autosimilarités peuvent être trouvés dans les articles sur l'escalier de Cantor et sur la fonction point d'interrogation de Minkowski. Précisément le même monoïde d'autosimilarités, le monoïde dyadique, s'applique à chaque courbe de De Rham.

Classification et exemples[modifier | modifier le code]

Les systèmes suivants génèrent des courbes continues.

Courbes de Cesàro[modifier | modifier le code]

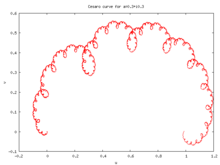
Les courbes de Cesàro, également connues sous le nom de courbes de Cesàro – Faber ou courbes en C de Lévy, sont des courbes de De Rham générées par des transformations affines conservant l'orientation, avec des points fixes en ${\displaystyle p_{0}=0}$ et ${\displaystyle p_{1}=1}$.

En raison de ces contraintes, les courbes de Cesàro sont déterminées de manière unique par un nombre complexe ${\displaystyle a}$ tel que ${\displaystyle |a|<1}$ et ${\displaystyle |1-a|<1}$.

Les applications contractantes ${\displaystyle d_{0}}$ et ${\displaystyle d_{1}}$ sont alors définies comme fonctions complexes dans le plan complexe par :

${\displaystyle d_{0}(z)=az\ ,\ d_{1}(z)=a+(1-a)z.}$

Pour la valeur de ${\displaystyle a=(1+\mathrm {i} )/2}$, la courbe résultante est la courbe en C de Lévy.

Courbes de Koch-Peano[modifier | modifier le code]

De la même manière, on peut définir la famille de courbes de Koch – Peano comme l'ensemble des courbes de De Rham générées par des transformations affines inversant l'orientation, avec des points fixes en ${\displaystyle p_{0}=0}$ et ${\displaystyle p_{1}=1}$.

Ces applications sont exprimées dans le plan complexe en fonction de ${\displaystyle {\overline {z}}}$, le complexe conjugué de ${\displaystyle z}$ :

${\displaystyle d_{0}(z)=a{\overline {z}}\ ,\ d_{1}(z)=a+(1-a){\overline {z}}.}$

Le nom de la famille vient de ses deux membres les plus célèbres. Le flocon de Koch est obtenue en fixant :

${\displaystyle a_{\text{Koch}}={\frac {1}{2}}+\mathrm {i} {\frac {\sqrt {3}}{6}},}$

tandis que la courbe de Peano correspond à :

${\displaystyle a_{\text{Peano}}={\frac {(1+i)}{2}}.}$

La courbe de De Rham pour ${\displaystyle a=(1+\mathrm {i} b)/2}$ pour les valeurs de ${\displaystyle b}$ inférieures et proches de 1 ressemble visuellement à la courbe d'Osgood (en). Ces deux courbes sont étroitement liées, mais ne sont pas identiques. La courbe d'Osgood est obtenue par soustraction d'ensembles répétés et constitue donc un ensemble parfait, tout comme l'ensemble de Cantor lui-même. La construction de l'ensemble d'Osgood demande que des triangles de plus en plus petits soient soustraits, laissant derrière eux un ensemble « gros » de mesure non nulle ; la construction est analogue à l'ensemble gras de Cantor, qui a une mesure non nulle. En revanche, la courbe de De Rham n’est pas « grosse » ; la construction n'offre pas de moyen de « grossir » les « segments de droite » qui se situent « entre » les rationnels dyadiques.

Applications affines générales[modifier | modifier le code]

Les courbes de Cesàro–Faber et de Peano–Koch sont toutes deux des cas particuliers du cas général d'une paire de transformations linéaires affines sur le plan complexe. En fixant une extrémité de la courbe à 0 et l'autre à 1, le cas général est obtenu en itérant sur les deux transformées

${\displaystyle d_{0}={\begin{pmatrix}1&0&0\\0&\alpha &\delta \\0&\beta &\varepsilon \end{pmatrix}}\ ,\ d_{1}={\begin{pmatrix}1&0&0\\\alpha &1-\alpha &\zeta \\\beta &-\beta &\eta \end{pmatrix}}.}$

Étant des transformations affines, ces transformations agissent sur un point ${\displaystyle (u,v)}$ du plan 2D en agissant sur le vecteur

${\displaystyle {\begin{pmatrix}1\\u\\v\end{pmatrix}}.}$

On voit que le milieu de la courbe se situe en ${\displaystyle (u,v)=(\alpha ,\beta )}$ ; les quatre autres paramètres peuvent varier pour créer une grande variété de courbes.

La courbe du blanc-manger du paramètre ${\displaystyle w}$ peut être obtenu en définissant ${\displaystyle \alpha =\beta =1/2}$, ${\displaystyle \delta =\zeta =0}$ et ${\displaystyle \varepsilon =\eta =w}$, soit :

${\displaystyle d_{0}={\begin{pmatrix}1&0&0\\0&1/2&0\\0&1/2&w\end{pmatrix}}\ ,\ d_{1}={\begin{pmatrix}1&0&0\\1/2&1/2&0\\1/2&-1/2&w\end{pmatrix}}.}$

Depuis la courbe du blanc-manger pour le paramètre ${\displaystyle w=1/4}$ est une parabole de l'équation ${\displaystyle f(x)=4x(1-x)}$, cela illustre le fait que dans certaines occasions, les courbes de De Rham peuvent être lisses.

Fonction point d'interrogation de Minkowski[modifier | modifier le code]

La fonction point d'interrogation de Minkowski est générée par la paire d'applications

${\displaystyle d_{0}(z)={\frac {z}{z+1}}\ ,\ d_{1}(z)={\frac {1}{2-z}}.}$

Non-exemples[modifier | modifier le code]

Étant donné deux fonctions quelconques ${\displaystyle d_{0}}$ et ${\displaystyle d_{1}}$, on peut définir une application à partir de l'espace de Cantor, par itération répétée des chiffres, exactement de la même manière que pour les courbes de De Rham. En général, le résultat ne sera pas une courbe de De Rham si les conditions de continuité ne sont pas remplies. Ainsi, il existe de nombreux ensembles qui pourraient être en correspondance biunivoque avec l'espace de Cantor, dont les points peuvent être associés de manière unique avec des points dans l'espace de Cantor ; cependant, ce ne sont pas des courbes de De Rham, car les rationnels dyadiques ne correspondraient pas au même point.

Ensemble de Julia de l'ensemble de Mandelbrot[modifier | modifier le code]

L'ensemble de Mandelbrot est généré par une équation itérée de doublement de période ${\displaystyle z_{n+1}=z_{n}^{2}+c.}$ L'ensemble de Julia correspondant est obtenu en itérant dans la direction opposée. Cela se fait en écrivant ${\displaystyle z_{n}=\pm {\sqrt {z_{n+1}-c}}}$, ce qui donne deux racines distinctes déduites de l'itération avant ${\displaystyle z_{n+1}}$. Ces deux racines peuvent être distinguées comme

${\displaystyle d_{0}(z)=+{\sqrt {z-c}}\ ,\ d_{1}(z)=-{\sqrt {z-c}}.}$

En fixant du nombre complexe ${\displaystyle c}$, le résultat est l'ensemble de Julia pour cette valeur de ${\displaystyle c}$. Cette courbe est continue lorsque ${\displaystyle c}$ est à l'intérieur de l'ensemble de Mandelbrot ; sinon, c'est un nuage de points déconnectés. Cependant, la raison de la continuité n'est pas due à la condition de De Rham, car, en général, les points correspondant aux rationnels dyadiques sont très éloignés les uns des autres. En fait, cette propriété peut être utilisée pour définir une notion de « pôles opposés », de points conjugués dans l'ensemble de Julia.

Généralisations[modifier | modifier le code]

Il est facile de généraliser la définition en utilisant plus de deux applications de contraction. Si l'on utilise n applications, alors la décomposition n-aire de x doit être utilisée à la place du développement binaire des nombres réels. La condition de continuité doit être généralisée en :

${\displaystyle d_{i}(p_{n-1})=d_{i+1}(p_{0})}$, pour ${\displaystyle i=0\ldots n-2.}$

Cette condition de continuité peut être comprise avec l’exemple suivant. Supposons que l'on travaille en base 10. Ensuite, on a (classiquement) la correspondance 0,999...= 1,000... ce qui est une équation de continuité qui doit être appliquée à chaque écart de ce type. Autrement dit, étant donné les chiffres décimaux ${\displaystyle b_{1},b_{2},\cdots ,b_{k}}$ avec ${\displaystyle b_{k}\neq 9}$, on a

${\displaystyle b_{1},b_{2},\cdots ,b_{k},9,9,9,\cdots =b_{1},b_{2},\cdots ,b_{k}+1,0,0,0,\cdots }$

Une telle généralisation permet, par exemple, de produire la courbe en pointe de flèche de Sierpiński (dont l'image est le triangle de Sierpiński ), en utilisant les applications de contraction d'un système de fonctions itérées qui produit le triangle de Sierpiński.

Courbes multifractales[modifier | modifier le code]

Ornstein et d'autres décrivent un système multifractal dans lequel, au lieu de travailler sur une base fixe, on travaille sur une base variable.

On considère l'espace produit d'espaces discrets des bases variables ${\displaystyle m_{n}}$

${\displaystyle \Omega =\prod _{n\in \mathbb {N} }A_{n}}$

pour ${\displaystyle A_{n}=\mathbb {Z} /m_{n}\mathbb {Z} =\{0,1,\cdots ,m_{n}-1\}}$ le groupe cyclique, pour ${\displaystyle m_{n}\geq 2}$ un nombre entier. Tout nombre réel dans l'intervalle unité peut être développé en une suite${\displaystyle (a_{1},a_{2},a_{3},\cdots )}$ telle que chaque ${\displaystyle a_{n}\in A_{n}}$. Plus précisément, un nombre réel ${\displaystyle 0\leq x\leq 1}$ s'écrit comme

${\displaystyle x=\sum _{n=1}^{\infty }{\frac {a_{n}}{\prod _{k=1}^{n}m_{k}}}}$

Ce développement n'est pas unique, si ${\displaystyle a_{n}=0}$ pour tout ${\displaystyle K<n}$. Dans ce cas, on a :

${\displaystyle a_{1},a_{2},\cdots ,a_{K},0,0,\cdots =a_{1},a_{2},\cdots ,a_{K}-1,m_{K+1}-1,m_{K+2}-1,\cdots }$

De tels points sont analogues aux rationnels dyadiques dans le développement dyadique, et les équations de continuité sur la courbe doivent être appliquées à ces points.

Pour chaque ${\displaystyle A_{n}}$, il faut préciser deux choses : un ensemble de deux points ${\displaystyle p_{0}^{(n)}}$ et ${\displaystyle p_{1}^{(n)}}$ et un ensemble de ${\displaystyle m_{n}}$ fonctions ${\displaystyle d_{j}^{(n)}(z)}$ (avec ${\displaystyle j\in A_{n}}$ ). La condition de continuité est alors comme ci-dessus,

${\displaystyle d_{j}^{(n)}(p_{1}^{(n+1)})=d_{j+1}^{(n)}(p_{0}^{(n+1)})}$, pour ${\displaystyle j=0,\cdots ,m_{n}-2.}$

Dans son exemple original, Ornstein utilise

${\displaystyle \Omega =\left(\mathbb {Z} /2\mathbb {Z} \right)\times \left(\mathbb {Z} /3\mathbb {Z} \right)\times \left(\mathbb {Z} /4\mathbb {Z} \right)\times \cdots }$

Voir également[modifier | modifier le code]

• Système de fonctions itérées
• Fonction raffinable (en)
• Groupe modulaire
• Groupe fuchsien (en)

Références[modifier | modifier le code]

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « De Rham curve » (voir la liste des auteurs).

Bibliographie[modifier | modifier le code]

• (en) Georges de Rham, On Some Curves Defined by Functional Equations (1957), reprinted in Classics on Fractals, ed. Gerald A. Edgar (Addison-Wesley, 1993), pp. 285–298.
• (en) Linas Vepstas, A Gallery of de Rham curves, (2006).
• (en) Linas Vepstas, Symmetries of Period-Doubling Maps, (2006). (A general exploration of the modular group symmetry in fractal curves.)

• Portail de l'analyse
• Portail de la géométrie