Théorème de l'angle inscrit et de l'angle au centre

En géométrie euclidienne plane, plus précisément dans la géométrie du cercle, les théorèmes de l'angle inscrit et de l'angle au centre établissent des relations liant les angles inscrits^[1] et les angles au centre interceptant un même arc.

Le théorème de l'angle au centre affirme que, dans un cercle, un angle au centre mesure le double d'un angle inscrit interceptant le même arc (figure 1 et 2, $2{\widehat {AMB}}={\widehat {AOB}}$ ).
Le théorème de l'angle inscrit est une conséquence du précédent et affirme que deux angles inscrits interceptant le même arc de cercle ont la même mesure (figure 1).

Il existe deux versions de ces théorèmes, une concernant les angles géométriques et l'autre les angles orientés.

Théorème de l'angle au centre[modifier | modifier le code]

Version relative aux angles géométriques[modifier | modifier le code]

Théorème^[2] — Soit M un point d'un cercle Γ, de centre O, A et B sont deux points du cercle distincts de M. Si les angles AMB et AOB interceptent le même arc AB alors : $2{\widehat {AMB}}={\widehat {AOB}}$ .

Il existe donc deux situations, l'une où l'angle inscrit de sommet M est aigu, donc l'angle au centre de sommet O saillant (figure 1), l'autre où l'angle inscrit de sommet M est obtus, donc l'angle au centre de sommet O rentrant (figure 2).

Cas particulier[modifier | modifier le code]

Le cas d'un angle inscrit dans un demi-cercle est le cas particulier pour lequel l'angle au centre est un angle plat, et donc l'angle inscrit est un angle droit.

Version relative aux angles orientés[modifier | modifier le code]

L'énoncé et la démonstration de la propriété sont beaucoup plus simples avec des angles orientés.

Théorème^[3] — Soient A, B et M trois points distincts, et Γ un cercle de centre O passant par A et B. Le point M appartient à Γ si et seulement si : $({\overrightarrow {OA}},{\overrightarrow {OB}})\equiv 2({\overrightarrow {MA}},{\overrightarrow {MB}})\mod {2\pi }$ .

Théorème de l'angle inscrit[modifier | modifier le code]

Version relative aux angles géométriques[modifier | modifier le code]

Corollaire — Deux angles inscrits dans un cercle et interceptant le même arc sont de même mesure.

Cette propriété est une conséquence immédiate^[2] du théorème de l'angle au centre ci-dessus.

Complément — Deux angles inscrits dans un cercle interceptant des arcs de cercle complémentaires^[4] sont supplémentaires.

Les angles inscrits interceptent deux arcs complémentaires si leurs sommets sont de part et d'autre de la corde associée aux deux arcs.

La propriété énoncée est encore une conséquence directe du théorème de l'angle au centre. Lorsque les arcs sont complémentaires, la somme des angles au centre donne un angle plein. Comme les angles inscrits valent moitié des angles au centre, la somme des angles inscrits donne un angle plat.

Applications[modifier | modifier le code]

Ce théorème est à la base de la notion de cercle de focalisation, ou cercle de Rowland, en spectrométrie.

Article détaillé : Focalisation (optique)#Analyse spectrale par un réseau courbe.

Angle de la corde et d'une tangente[modifier | modifier le code]

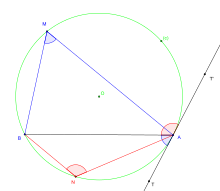
La propriété des angles inscrits se généralise aux angles que fait la corde qui sous-tend l'arc avec une tangente :

L'angle inscrit a même mesure que l'angle formé par la corde, qui joint les extrémités de l'arc, avec la partie de la tangente au cercle à l'une des extrémités de la corde, située à l'opposé de l'angle en question par rapport à la corde.

L'angle inscrit ${\widehat {AMB}}$ a même mesure que celle d'un des deux angles formés par la tangente (TT') au cercle en A avec la corde [AB] :

L'angle inscrit ${\widehat {AMB}}$ est de même mesure que l'angle ${\widehat {BAT}}$ de la corde [BA] avec la tangente [AT).

${\widehat {BAT}}$ est la position limite de l'angle inscrit ${\widehat {BMA}}$ lorsque M « tend » vers A.

Démonstration

Si H est le milieu de [AB], les angles ${\widehat {HOA}}$ et ${\widehat {BAT}}$ ont leurs côtés deux à deux perpendiculaires, ils ont même mesure.

(OH) étant la bissectrice du triangle isocèle BOA, on a ${\widehat {HOA}}={\frac {1}{2}}{\widehat {BOA}}$ et ${\widehat {BAT}}$ est bien égal à la moitié de la mesure de l'angle au centre ${\widehat {BOA}}$ et donc à la mesure de l'angle ${\widehat {BMA}}$ d'après le théorème de l'angle au centre.

Version relative aux angles orientés[modifier | modifier le code]

Pour les angles orientés, la propriété devient une caractérisation du cercle passant par les points A, M et B.

Théorème — Si $\Gamma$ est le cercle circonscrit à un triangle non plat AMB alors pour tout point N distinct de A et B, on a

({\overrightarrow {NA}},{\overrightarrow {NB}})\equiv ({\overrightarrow {MA}},{\overrightarrow {MB}})\mod \pi \iff N\in \Gamma

.

On remarquera que l'égalité n'est vraie qu'à $π$ près, ce qui explique que les angles géométriques puissent être supplémentaires.

Application à l'angle entre deux cordes sécantes[modifier | modifier le code]

Théorème de l'angle entre deux cordes sécantes : l'angle entre deux cordes sécantes est égal à la moyenne des angles au centre interceptés ; avec les notations de la figure : ${\widehat {AMB'}}={\widehat {A'MB}}={\frac {1}{2}}({\widehat {AOB'}}+{\widehat {A'OB}})$ .

Démonstration :

D'après le théorème de l'angle inscrit, ${\widehat {A'AB}}={\widehat {A'B'B}}=\alpha$ et ${\widehat {AA'B'}}={\widehat {ABB'}}=\beta$ , et d'après la propriété des angles du triangle $AMA'$ (ou $BMB'$ ) , ${\widehat {AMB'}}=\alpha +\beta$ ; or $\alpha ={\frac {1}{2}}{\widehat {A'OB}}$ et $\beta ={\frac {1}{2}}{\widehat {AOB'}}$ d'où le résultat.

On en déduit que si les cordes sont perpendiculaires, on a la relation entre longueurs d'arcs : ${\overset {\frown }{AA'}}+{\overset {\frown }{BB'}}={\overset {\frown }{A'B}}+{\overset {\frown }{B'A}}=\pi R$ , relation connue d'Archimède ^[5].

Notes et références[modifier | modifier le code]

Cet article est partiellement ou en totalité issu de l'article intitulé « Théorème de l'angle inscrit » (voir la liste des auteurs).

↑ Un angle inscrit est un angle dont le sommet appartient au cercle. Ainsi, sur le schéma, l'angle AMO est inscrit au cercle car M est placé sur la circonférence.
↑ ^{a et b} Pour une démonstration, voir par exemple le chapitre « Angle inscrit et angle au centre » de la leçon « Théorème de l'angle inscrit » sur Wikiversité.
↑ Pour une démonstration, voir par exemple le chapitre « Version relative aux angles orientés » de la leçon « Théorème de l'angle inscrit » sur Wikiversité.
↑ Un des arcs, complété par l'autre, forme le cercle tout entier. Voir Complémentaire (théorie des ensembles).
↑ David wells, Le dictionnaire Penguin des curiosités géométriques, Eyrolles, 1998, p. 107

Voir aussi[modifier | modifier le code]

Sur les autres projets Wikimedia :

Théorème de l'angle inscrit, sur Wikiversity

Portail de la géométrie

[1] Un angle inscrit est un angle dont le sommet appartient au cercle. Ainsi, sur le schéma, l'angle AMO est inscrit au cercle car M est placé sur la circonférence.

[Wikiversité1-2] {a et b} Pour une démonstration, voir par exemple le chapitre « Angle inscrit et angle au centre » de la leçon « Théorème de l'angle inscrit » sur Wikiversité.

[Wikiversité2-3] Pour une démonstration, voir par exemple le chapitre « Version relative aux angles orientés » de la leçon « Théorème de l'angle inscrit » sur Wikiversité.

[4] Un des arcs, complété par l'autre, forme le cercle tout entier. Voir Complémentaire (théorie des ensembles).

[5] David wells, Le dictionnaire Penguin des curiosités géométriques, Eyrolles, 1998, p. 107

[1]

[2]

[3]

[4]

[5]

Théorème de l'angle inscrit et de l'angle au centre

Théorème de l'angle au centre[modifier | modifier le code]

Version relative aux angles géométriques[modifier | modifier le code]

Cas particulier[modifier | modifier le code]

Version relative aux angles orientés[modifier | modifier le code]

Théorème de l'angle inscrit[modifier | modifier le code]

Version relative aux angles géométriques[modifier | modifier le code]

Applications[modifier | modifier le code]

Angle de la corde et d'une tangente[modifier | modifier le code]

Version relative aux angles orientés[modifier | modifier le code]

Application à l'angle entre deux cordes sécantes[modifier | modifier le code]

Notes et références[modifier | modifier le code]

Voir aussi[modifier | modifier le code]

€4.95