Toro (geometría)

R > r:
Toro de anillo

R = r:
Toro de cuerno

R < r:
Toro de huso

Mitades inferiores y secciones longitudinales de las tres clases de toro.

En geometría, un toro es un tipo concreto de toroide cuya superficie de revolución es generada por una circunferencia que gira alrededor de una recta exterior coplanaria (en su plano y que no la corta)^[1]​ o, llanamente, la superficie tridimensional que resulta de hacer girar una circunferencia alrededor de un eje que no la corta. La palabra «toro» proviene del latín torus, que significa «protuberancia», «elevación curva» (relacionado con latín sterno y griego στορέννυμι, romanizado storénnymi) y que ya en latín adquiere sentidos técnicos para designar objetos con esta forma geométrica específica, por ejemplo en arquitectura (Vitr.3.3.8), donde designa el «bocel» o «murecillo», que es una moldura redondeada de la base, con forma de hogaza de pan.^[2]​ Muchos objetos cotidianos tienen forma de toro: una rosquilla, una cámara de neumático, etc.

Geometría[editar]

Las ecuaciones paramétricas que lo definen son:

${\displaystyle {\begin{cases}x=\cos \theta \cdot (R+r\cos \varphi )\\y=\operatorname {sen} \theta \cdot (R+r\cos \varphi )\\z=r\operatorname {sen} \varphi \end{cases}}}$

donde ${\displaystyle R}$ es el trayecto entre el centro del conducto y el centro del toro, ${\displaystyle r}$ es el radio del conducto, ambas constantes con ${\displaystyle r<R}$ y donde ${\displaystyle \theta ,\varphi \in [0,2\pi )}$ son ángulos que determinan el círculo completo.

La ecuación en coordenadas cartesianas de un toro cuyo eje es el eje z es:

${\displaystyle \left(R-{\sqrt {x^{2}+y^{2}}}\right)^{2}+z^{2}=r^{2}}$

La superficie A y el volumen V del toro pueden hallarse empleando el teorema de Papus de Alejandría. Los resultados son:

${\displaystyle A=4\pi ^{2}Rr\,}$

${\displaystyle V=2\pi ^{2}Rr^{2}\,}$, donde ${\displaystyle R}$ es la distancia del eje de revolución al centro de una sección circular del toro y ${\displaystyle r}$ es el radio de dicha sección.

${\displaystyle A=\pi ^{2}Dd\,}$

${\displaystyle V={\frac {1}{4}}\pi ^{2}Dd^{2}\,}$ usando los respectivos diámetros :${\displaystyle D=2R,d=2r}$

Topología[editar]

Topológicamente, un toro es una superficie cerrada definida como el producto cartesiano de dos circunferencias: ${\displaystyle S^{1}\times S^{1}}$ y con la topología producto. Equivalentemente, un toro es una superficie cerrada orientable de género 1. Esta equivalencia se obtiene gracias al teorema de clasificación de superficies cerradas.

En topología, un «volumen tórico» o «toro sólido» (vollringe) es un objeto tridimensional obtenido mediante el producto cartesiano de un disco y una circunferencia: ${\displaystyle D^{2}\times S^{1}}$

La superficie descrita, dada la topología relativa de R³, es homeomorfa con el toro topológico mientras este no intercepte con su propio eje.

El toro puede también describirse como el cociente del ’’plano euclidiano’’ bajo las tipificaciones

(x, y) ~ (x+1,y) ~ (x, y+1)

Equivalentemente, como el cociente del cuadrado o unidad conectando los bordes opuestos, descrito como un polígono fundamental ${\displaystyle ABA^{-1}B^{-1}}$.

Esta superficie se considera como el espacio total de un fibrado (trivial), donde el espacio base es la circunferencia ${\displaystyle S^{1}}$.

El grupo fundamental del toro es precisamente el producto directo del grupo fundamental de la circunferencia por sí misma:

${\displaystyle \pi _{1}(\mathbb {T} ^{2})=\pi _{1}(S^{1})\times \pi _{1}(S^{1})\cong \mathbb {Z} \times \mathbb {Z} }$

Intuitivamente, esto significa que un camino cerrado el cual rodea entre ambos, el «orificio» y el «cuerpo» del toro (ambos de circunferencia con latitud concreta), se puede transformar en un camino que envuelva el cuerpo y el orificio. Es decir, los caminos estrictamente meridionales y estrictamente longitudinales participan en operaciones conmutativas.

El primer grupo homológico del toro es isomorfo al grupo fundamental; puesto que el grupo fundamental es abeliano).

Toro plano[editar]

Un toro plano es un toro con la métrica heredada de su representación como cociente, ${\displaystyle \mathbb {R} ^{2}}$/L, donde L es un subgrupo discreto de ${\displaystyle \mathbb {R} ^{2}}$ isomorfo a ${\displaystyle \mathbb {Z} ^{2}}$. Esto le da al cociente la estructura de una variedad de Riemann. Quizás el ejemplo más simple de esto sea cuando L= ${\displaystyle \mathbb {Z} ^{2}}$: ${\displaystyle \mathbb {R} ^{2}/\mathbb {Z} ^{2}}$, que también puede describirse como un sistema de coordenadas cartesianas bajo las identificaciones (x, y) ~ (x + 1, y) ~ (x, y + 1). Este toro plano en particular (y cualquier versión del mismo con escala uniforme) se conoce como toro plano "cuadrado".

Esta métrica del toro cuadrado plano también se puede realizar mediante incrustaciones específicas del familiar 2-toro en espacios euclídeos de 4 o más dimensiones. Su superficie tiene curvatura de Gauss cero en todas partes. Su superficie es plana en el mismo sentido que la superficie de un cilindro es plana. En 3 dimensiones, se puede doblar una hoja plana de papel hasta formar un cilindro sin estirar el papel, pero este cilindro no se puede doblar hasta formar un toro sin estirar el papel (a menos que se abandonen algunas condiciones de regularidad y diferenciabilidad, véase más abajo).

Un embebido euclídeo simple de 4 dimensiones de un toro plano rectangular (más general que el cuadrado) es el siguiente:

${\displaystyle (x,y,z,w)=(R\cos u,R\sin u,P\cos v,P\sin v)}$

donde R y P son constantes positivas que determinan la relación de aspecto. Es difeomórfico para un toro normal, pero no isométrico. No se puede incrustar analíticamente (mediante una función suave de clase C^k, 2 ≤ k ≤ ∞) en el espacio tridimensional euclidiano. Una aplicación en el espacio tridimensional requiere que la figura se estire, en cuyo caso se parece a un toroide normal. Por ejemplo, en la siguiente aplicación:

${\displaystyle (x,y,z)=((R+P\sin v)\cos u,(R+P\sin v)\sin u,P\cos v).}$

Si R y P en la parametrización del toro plano anterior forman un vector unitario (R, P)= (cos(η), sin(η)), entonces u, v y 0 < η < Plantilla:Pi/2 parametrizan la 3-esfera unidad como un sistema de coordenadas de Hopf. En particular, para ciertas opciones muy específicas de un toro plano cuadrado en la 3-esfera S³, donde η= Plantilla:Pi/4 como arriba, el toro dividirá la 3-esfera en dos subconjuntos de toros sólidos congruentes con la superficie del toro plano antes mencionada como su frontera común. Un ejemplo es el toro T definido por

${\displaystyle T=\left\{(x,y,z,w)\in \mathbb {S} ^{3}\mid x^{2}+y^{2}={\frac {1}{2}},\ z^{2}+w^{2}={\frac {1}{2}}\right\}.}$

Otros toros en S³ que tienen esta propiedad de partición incluyen los toros cuadrados de la forma Q⋅T', donde Q es una rotación del espacio de 4 dimensiones ${\displaystyle \mathbb {R} ^{4}}$, o en otras palabras, Q es miembro del grupo de Lie SO(4).

Se sabe que no existe ninguna incrustación C² (dos veces diferenciable continuamente) de un toro plano en el 3-espacio (la idea de la demostración es tomar una esfera grande que contenga un toro plano en su interior y reducir el radio de la esfera hasta que toque el toro por primera vez). Tal punto de contacto debe ser una tangencia. Pero eso implicaría que parte del toro, dado que tiene curvatura cero en todas partes, debe quedar estrictamente fuera de la esfera, lo cual es una contradicción. Por otro lado, según el teorema de Nash-Kuiper, que fue probado en la década de 1950, existe un embebido isométrico C¹. Esto es únicamente una prueba de existencia y no proporciona ecuaciones explícitas para dicha incorporación.

En abril de 2012, se encontró un embebido explícito C¹ (continuamente diferenciable) de un toro plano en el espacio euclídeo tridimensional ${\displaystyle \mathbb {R} ^{3}}$.^[3]​^[4]​^[5]​^[6]​ Es un toro plano en el sentido de que, como espacios métricos, es isométrico a un toro cuadrado plano. Tiene una estructura similar a un fractal, ya que se construye corrugando repetidamente un toro común. Al igual que los fractales, no tiene una curvatura gaussiana definida. Sin embargo, a diferencia de los fractales, tiene definidas las normales a la supoerficie, lo que produce el llamado "fractal suave". La clave para obtener la suavidad de este toro corrugado es hacer que las amplitudes de las corrugaciones sucesivas disminuyan más rápido que sus "longitudes de onda".^[7]​ Estas corrugaciones infinitamente recursivas se utilizan solo para incrustaciones en tres dimensiones, y no son una característica intrínseca del toro plano. Esta es la primera vez que dicha incrustación se define mediante ecuaciones explícitas o se representa mediante gráficos por computadora.

Clasificación conforme de toro plano[editar]

En el estudio de superficies de Riemann, se dice que dos superficies geométricas compactas y lisas son "conformemente equivalentes" cuando existe un homeomorfismo suave entre ellas que preserva el ángulo y la orientación. El teorema de uniformización garantiza que cada superficie de Riemann es conformemente equivalente a una que tiene curvatura gaussiana constante. En el caso de un toro, la curvatura constante debe ser cero. Luego se define el "espacio de módulos" del toro para que contenga un punto para cada clase de equivalencia conforme, con la topología adecuada. Resulta que este espacio de módulos M puede identificarse con una esfera perforada que es lisa excepto por dos puntos que tienen un ángulo menor que 2π (radianes) a su alrededor: uno tiene π y el otro tiene 2π/3.

M puede convertirse en un espacio compacto M* añadiendo un punto adicional que represente el caso límite cuando un toro rectangular se aproxima a una relación de aspecto de 0 en el límite. El resultado es que este espacio de módulos compactado es una esfera con "tres" puntos, cada uno de los cuales tiene un ángulo inferior a 2π alrededor de ellos (dichos puntos se denominan "cúspides"). Este punto adicional tendrá un ángulo cero a su alrededor. Debido a la simetría, M* se puede construir pegando dos triángulos geodésicos congruentes en el plano hiperbólico en sus límites (idénticos), donde cada triángulo tiene ángulos de π/2, π/3 y 0. Como resultado, el área de cada triángulo se puede calcular como π - (π/2 + π/3 + 0) = π/6, por lo que se deduce que el espacio de módulos compactados M* tiene un área igual a π/3.

Las otras dos cúspides se localizan en los puntos correspondientes en M* a a) el toro cuadrado (π) y b) el toro hexagonal (2π/3). Estas son las únicas clases de equivalencia conforme de toros planos que tienen automorfismos conformes distintos de los generados por traslaciones y negación.

El toro en n dimensiones[editar]

Se puede generalizar fácilmente el toro a cualquier dimensión o potencia. Un toro n dimensional se define como el producto de n circunferencias:

${\displaystyle \mathbb {T} ^{n}=S^{1}\times S^{1}\times \cdots \times S^{1}}$

• el “toro a la 1” es precisamente la circunferencia: ${\displaystyle S^{1}}$.
• el ${\displaystyle \mathbb {T} ^{2}=S^{1}\times S^{1}}$ es el “toro a la 2”,
• el “toro a la 3” puede considerarse como ${\displaystyle \mathbb {T} ^{2}\times S^{1}}$, esto es como el producto cartesiano del dos-toro por la circunferencia.
• generalizando, el toro a la n potencia puede describirse como el cociente de Rⁿ con desplazamientos enteros sobre cualquier coordenada.

El toro a la n es Rⁿ módulo la acción del grupo enrejado Zⁿ (con la acción considerada como suma de vectores). Equivalentemente, el toro a la n se obtiene a partir del n-cubo pegando las caras opuestas.

Los grupos toroidales desempeñan un papel importante en la teoría de grupos compactos de Lie. Esto se debe en parte al hecho de que en cualquier grupo compacto de Lie, se puede encontrar un toro máximo; es decir, un subgrupo cerrado, el cual es un determinado toro de la mayor dimensión posible.

El grupo fundamental de un toro a la n es un grupo abeliano libre de rango n. El k-ésimo grupo homológico de un toro a la n es un grupo abeliano libre de rango n sobre k. De esto se deduce que la característica de Euler del toro a la n es 0 para cualquier n. El anillo homológico H^•(Tⁿ,Z) puede identificarse con el álgebra exterior sobre Z-módulo Zⁿ cuyos generadores son los números duales enteros de los ciclos fundamentales a la potencia n.

Aplicaciones[editar]

Matemática[editar]

Si se toma idealmente una superficie rectangular flexible y extensible y se unen su lado superior con su lado inferior, y luego se unen los lados horizontales, resulta esta figura. Uno debe respetar en el pegado la orientación de los bordes como el indicado en la figura.

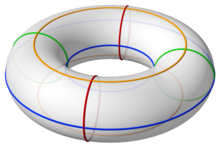
Algunos teoremas de geometría plana no son válidos si consideramos el trazado de puntos y curvas sobre la superficie del toro. Por ejemplo, el teorema de los cuatro colores se convierte en teorema de los siete colores y es mucho más fácil de probar. En la figura anterior se observa que son necesarios siete colores.

Física[editar]

En magnetismo, se enrolla una bobina con cierta cantidad de vueltas sobre el toro con un entrehierro (corte paralelo al eje que pasa por el centro del toro) para generar un campo magnético dentro del mismo. Esto se suele hacer para crear un imán; se coloca un material ferromagnético en el entrehierro y se imprime una corriente eléctrica por la bobina. Una vez que se alcanza la saturación del material, se lo retira y este queda magnetizado, formando un imán.

Uno de los sistemas más promisorios para obtener electricidad a partir de la fusión nuclear controlada se basa en el confinamiento magnético del plasma a elevadísimas temperaturas dentro de un espacio-circuito toroidal como el tokamak o el Thorus, también muchos aceleradores de partículas recurren a una forma cuasi toroidal.

Óptica[editar]

En el campo de la óptica, se usa la lente tórica para corregir el astigmatismo tienen una superficie tórica, que presenta dos curvaturas en orientaciones perpendiculares entre sí.

Videojuegos[editar]

En el mundo de los videojuegos de estrategia es fácil observar cómo los personajes que intervienen, cuando viajan hacia el norte reaparecen en el sur, como si le hubiesen dado la vuelta al mundo. Asimismo, cuando llevan una trayectoria hacia el fondo en el oriente, reaparecen en el occidente y viceversa. El sitio virtual donde este efecto acaece lleva el nombre de mundo toroide por las características matemáticas anteriormente descritas. El jugador siente la pseudoimpresión de un mundo esférico aunque el terreno de juego este pensado como un plano rectangular.

Galería[editar]

• 
  Intersección de un toro y un plano.
• 
  Animación de un toro cortado por un plano, y creación de Círculos de Villarceau. Ver Vesica piscis.
• 
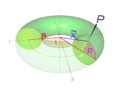
  Ilustración de un toro con sus principales variables.
• 
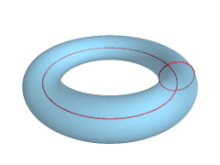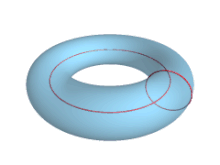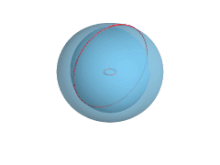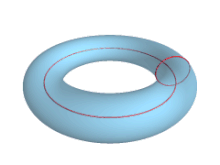
  Una geodésica cerrada del toro.

Véase también[editar]

• Portal:Geometría. Contenido relacionado con Geometría.
• Portal:Matemáticas. Contenido relacionado con Matemáticas.
• Toroide
• Toro de Clifford
• Corona circular
• Óvalo de Cassini
• Spira de Perseo
• Curva elíptica
• Período de enrejado
• Fibrado de Seifert

Referencias[editar]

Bibliografía[editar]

• Kozak, Ana María; Pompeya Pastorelli, Sonia; Verdanega, Pedro Emilio. Nociones de Geometría Analítica y Álgebra Lineal (2007 edición). McGraw-Hill. p. 744. ISBN 9789701065969. 
• Allen Hatcher. Algebraic topology. Cambridge University Press, 2002. ISBN 0-521-79540-0. (en inglés)
• V.V. Nikulin, I.R.Shafarevich. Geometries and Groups. Springer, 1987. ISBN 3540152814, ISBN 9783540152811. (en inglés)

Enlaces externos[editar]

• Wikimedia Commons alberga una categoría multimedia sobre Toro.
• Wikcionario tiene definiciones y otra información sobre toro.
• Weisstein, Eric W. «Torus». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Creation of a torus ( de Alexander Bogomolny Cut the Knot) — una animación el formato AVI.
• More Torus Images (de Math is Fun)
• Torus Games Juegos de descarga gratuita para Windows y Mac OS sobre la topología del toro.