Wissenschaftliches Werk Leonhard Eulers

Das wissenschaftliche Werk von Leonhard Euler ist das umfangreichste von einem Mathematiker jemals geschaffene. Es umfasst unter anderem grundlegende Resultate in den Bereichen Infinitesimalrechnung, Analysis, Mechanik, Astronomie, Geodäsie, Zahlentheorie, Algebra, Trigonometrie, Geometrie, Musiktheorie und Optik.

Zu Eulers berühmtesten Resultaten zählen die Lösung des Basler Problems, der Polyedersatz und die Eulersche Identität, wobei letztere eine enge Verbindung zwischen zahlreichen fundamentalen mathematischen Konstanten zieht. Für diese und andere Ergebnisse erhielt Euler auch posthum viele Ehrungen.

Eulers Forschung war sehr vielseitig. Er arbeitete in fast allen Bereichen der Mathematik und gilt als einer der produktivsten Mathematiker der Geschichte. Seine gesammelten Schriften der Opera omnia umfassen bisher 76 Bände. Insgesamt gibt es 866 Publikationen von ihm. Eulers Name ist mit einer großen Anzahl von Resultaten und wissenschaftlichen Themenbereichen verbunden.

Nach Leonhard Euler sind gleich zwei mathematische Konstanten benannt: die Eulersche Zahl ${\displaystyle \mathrm {e} \approx 2{,}71828}$ aus der Analysis (siehe Exponentialfunktion) und die Euler-Mascheroni-Konstante γ (Gamma) aus der Zahlentheorie, die manchmal nur als Eulersche Konstante bezeichnet wird und ungefähr gleich 0,57721 ist. Es ist nicht bekannt, ob γ rational oder irrational ist. Im Gegensatz dazu ist die Irrationalität der Zahl e bekannt und wurde zuerst von Euler gezeigt (siehe auch: Beweis der Irrationalität der eulerschen Zahl).

Eine breitere Leserschaft erlangte zudem seine populärwissenschaftliche Schrift Lettres à une princesse d’Allemagne von 1768, in der er in Form von Briefen an die Prinzessin Friederike Charlotte von Brandenburg-Schwedt, eine Nichte 2. Grades Friedrichs II., die Grundzüge der Physik, der Astronomie, der Mathematik, der Philosophie und der Theologie vermittelte.

Leonhard Eulers Werk beeinflusste viele Generationen an Mathematikern nachhaltig. So sagte Carl Friedrich Gauß: „Das Studium der Werke Eulers bleibt die beste Schule in den verschiedenen Gebieten der Mathematik und kann durch nichts anderes ersetzt werden“. Wegen der großen Zahl an Publikationen und Korrespondenzen zu anderen Mathematikern und Persönlichkeiten, ziehen sich Bestrebungen, ein Eulersches Gesamtwerk herauszugeben, bis in die heutige Zeit hinein. Durch die Herausgabe der Opera Omnia über die Euler-Kommission gilt dieses Unterfangen jedoch als weitestgehend umgesetzt.

Mathematische Notationen[Bearbeiten | Quelltext bearbeiten]

Euler führte in seinen zahlreichen Lehrbüchern mehrere Notationskonventionen ein. Durch die weite Verbreitung der Bücher setzten sich viele seiner Notationen nachhaltig durch. Er führte das Konzept der mathematischen Funktion ein^[1] und schrieb als erster f(x), um die Funktion f zu bezeichnen, die auf das Argument x angewandt wird. Der „formale“ von Euler verwendete Funktionsbegriff war ein wichtiger Meilenstein in Richtung der heutigen Definition:

Von ihm stammen auch die bis heute gebräuchlichen Notationen für die trigonometrischen Funktionen, der Buchstabe e für die Basis des natürlichen Logarithmus, der griechische Buchstabe Σ (Sigma) für Summen und der Buchstabe i zur Bezeichnung der imaginären Einheit;^[3] das Zeichen Δ (Delta) für die Differenz stammt ebenfalls von Euler.^[4] Die Verwendung des griechischen Buchstabens π zur Bezeichnung des Verhältnisses von Kreisumfang und -durchmesser (Kreiszahl) wurde ebenfalls von Euler popularisiert, obwohl sie ursprünglich auf den walisischen Mathematiker William Jones zurückgeht.^[5]

Analysis und Funktionentheorie[Bearbeiten | Quelltext bearbeiten]

Elementare Analysis[Bearbeiten | Quelltext bearbeiten]

Euler kann als einer der Begründer der Analysis angesehen werden. Der Mathematikhistoriker Thomas Sonar beschreibt in seinem Buch 3000 Jahre Analysis (2011) Leonhard Euler als einen „echten Giganten für die Analysis“. Eulers Bedeutung für dieses Feld wird nicht nur über die Einführung eines rigorosen Funktionsbegriffs hervorgehoben. So sei er „ungeschlagener Meister“ im Umgang mit Potenzreihen, die er als „unendliches Polynom verstanden“ zu seinem ständigen „Arbeitspferd“ machte.^[6]

Euler leistete Pionierarbeit bei der Verwendung analytischer Methoden zur Lösung von Problemen der Zahlentheorie. Damit vereinte er zwei ungleiche Zweige der Mathematik und führte ein neues Studiengebiet ein, die analytische Zahlentheorie.

Infinitesimalrechnung[Bearbeiten | Quelltext bearbeiten]

Wegen anhaltender Forschung war die Infinitesimalrechnung im 18. Jahrhundert auf dem Vormarsch. Insbesondere Eulers Freunde, die Bernoullis, waren für einen Großteil der frühen Fortschritte auf diesem Gebiet verantwortlich. Dank ihres Einflusses wurde das Studium der Infinitesimalrechnung zum Hauptschwerpunkt von Eulers Arbeit. In seinem Werk Institutiones calculi differentialis (1755) beschäftigte er sich systematisch mit der Differentialrechnung. Euler wählte die Interpretation: „Kleiner als jede angebbare Größe“ für infinitesimale Größen. In den Institutiones calculi differentialis aus dem Jahr 1755 definiert Euler:

Euler betrachtet also das Rechnen mit unendlich kleinen Größen als „Nullenrechnung“. Für diese führte er eine „unendlich kleine“ Größe ${\displaystyle \omega }$ und eine „unendlich große“ Größe ${\displaystyle i}$ (nicht zu verwechseln mit der imaginären Einheit) ein – und nutzte diese für Herleitungen korrekter Aussagen.^[7] So nutzte Euler mit ${\displaystyle x=\omega \cdot i}$ den für „eine zunächst beliebige Zahl ${\displaystyle k}$ gültigen Ansatz“

${\displaystyle a^{x}=\left(1+{\frac {kx}{i}}\right)^{i},}$

um die für die Eulersche Zahl ${\displaystyle \mathrm {e} }$ geltende Reihe

${\displaystyle \mathrm {e} =\sum _{n=0}^{\infty }{\frac {1}{n!}}}$

herzuleiten.^[8] Diese Formel liefert eine äußerst schnell konvergente Reihe für die Zahl ${\displaystyle \mathrm {e} }$, es gilt zum Beispiel

${\displaystyle 1+{\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{6}}+{\frac {1}{24}}+{\frac {1}{120}}+{\frac {1}{720}}=2{,}7180{\overline {5}}\approx 2{,}718281828...=\mathrm {e} .}$

Vor dem Hintergrund zu Eulers Formel für ${\displaystyle a^{x}}$ ist zu erwähnen, dass für ${\displaystyle k=\log(a)}$ der Grenzwert

${\displaystyle \lim _{n\to \infty }\left(1+{\frac {kx}{n}}\right)^{n}=(\mathrm {e} ^{\log(a)})^{x}=a^{x}}$

gültig ist, was seine ${\displaystyle i}$-Notation in die moderne Sprache eines mathematischen Limes einordnet.

Taylorreihen[Bearbeiten | Quelltext bearbeiten]

Euler ist in diesem Kontext für die Entwicklung und häufige Verwendung von Potenzreihen bekannt. Diese können als „unendlich lange Polynome“ aufgefasst werden, aus denen sich eine Funktion aus ihrem lokalen Verhalten (d. h. unter Kenntnis all ihrer Ableitungen und einem Punkt) in manchen Fällen „global rekonstruieren“ lässt. Unter anderem gab er direkte Beweise für Taylorreihen der Exponentialfunktion

${\displaystyle \mathrm {e} ^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+\dotsb }$

und der Arkustangensfunktion. Indirekte Beweise stammen von Newton^[9] und Leibniz aus der Zeit 1665 bis 1680. Ebenso entwickelte Euler die Sinus- und Kosinusfunktion in ihre Taylor-Reihen um den Entwicklungspunkt 0:

${\displaystyle \sin(x)=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{2n+1}}{(2n+1)!}},}$

${\displaystyle \cos(x)=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{2n}}{(2n)!}}.}$

Diese benutzte er, um mittels einfachen Einsetzens die Eulersche Formel für die Exponentialfunktion herzuleiten.

Unendliche Reihen[Bearbeiten | Quelltext bearbeiten]

1736 fand er (ebenfalls durch Verwendung von Potenzreihen) den lange gesuchten Grenzwert für die unendliche Summe der reziproken Quadratzahlen:

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}=1+{\frac {1}{4}}+{\frac {1}{9}}+\dotsb ={\frac {\pi ^{2}}{6}}.}$

Summiert man also „alle“ (unendlich vielen) Kehrwerte der Quadratzahlen auf, ist das Ergebnis die Zahl ${\displaystyle {\frac {\pi ^{2}}{6}}\approx 1{,}64493}$. Das bedeutet, dass für jede noch so kleine Zahl ${\displaystyle x>0}$ (etwa ${\displaystyle x=0{,}00001}$) eine Quadratzahl ${\displaystyle N^{2}}$ existiert, so dass für alle folgenden Quadratzahlen ${\displaystyle N^{2}<M^{2}}$ gilt

${\displaystyle {\frac {\pi ^{2}}{6}}-x<1+{\frac {1}{4}}+{\frac {1}{9}}+\cdots +{\frac {1}{N^{2}}}+{\frac {1}{(N+1)^{2}}}+\cdots +{\frac {1}{M^{2}}}<{\frac {\pi ^{2}}{6}}.}$

Da er für dieses Ergebnis bis dato nicht bekannte Manipulationstechniken für Potenzreihen verwendet hatte, wurde sein ursprünglicher Beweis nicht akzeptiert. Jedoch veröffentlichte Euler im Jahr 1743 einen anderen Beweis.^[10][11] Aus einer Verallgemeinerung dieses sogenannten Basler Problems leitete er eine geschlossene Darstellung für die geraden Bernoulli-Zahlen ${\displaystyle B_{2k}}$ ab. Er zeigte beispielsweise, dass die Summe der Kehrwerte aller vierten Potenzen und sechsten Potenzen ebenfalls gegen rationale Vielfache entsprechender Potenzen von ${\displaystyle \pi }$ streben.

${\displaystyle 1+{\frac {1}{2^{4}}}+{\frac {1}{3^{4}}}+\cdots ={\frac {\pi ^{4}}{90}},}$

${\displaystyle 1+{\frac {1}{2^{6}}}+{\frac {1}{3^{6}}}+\cdots ={\frac {\pi ^{6}}{945}},}$

und ganz allgemein

${\displaystyle \zeta (2k)=\sum _{n=1}^{\infty }{\frac {1}{n^{2k}}}=(-1)^{k-1}{\frac {(2\pi )^{2k}}{2(2k)!}}B_{2k}.}$

Diese galt sehr lange als beste Methode für die Berechnung der Bernoulli-Zahlen ${\displaystyle B_{k}}$.^[12]

Er nutzte die Identität

${\displaystyle {\frac {\pi }{4}}=5\arctan \left({\frac {1}{7}}\right)+2\arctan \left({\frac {3}{79}}\right),}$

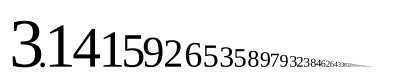
mit dem Arkustangens um eine schnell konvergierende Reihe für ${\displaystyle \pi }$ herzuleiten.^[13] Unendliche Reihen wie zum Beispiel

${\displaystyle 1+{\frac {1}{2}}-{\frac {1}{4}}-{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{8}}-\dotsb ={\frac {2\pi }{3{\sqrt {3}}}},}$

${\displaystyle 1-{\frac {1}{3^{3}}}+{\frac {1}{5^{3}}}-{\frac {1}{7^{3}}}+{\frac {1}{9^{3}}}-\dotsb ={\frac {\pi ^{3}}{32}},}$

oder auch

${\displaystyle {\frac {\zeta (2)}{3\cdot 4\cdot 2^{2}}}+{\frac {\zeta (4)}{5\cdot 6\cdot 2^{4}}}+{\frac {\zeta (6)}{7\cdot 8\cdot 2^{6}}}+\dotsb ={\frac {1}{4}}-{\frac {7}{4\pi ^{2}}}\zeta (3)}$

mit der Riemannschen Zeta-Funktion ${\displaystyle \zeta (s)}$ gehen ebenfalls auf Euler zurück.^[14][15] Es war Euler, der als erster divergente Reihen systematisch untersuchte.^[13]

Trigonometrische Funktionen[Bearbeiten | Quelltext bearbeiten]

Euler ist der erste Autor, der die Winkelfunktionen auf einen Kreis mit Radius 1 bezieht und sie dadurch normiert. Das geschieht im sechsten Kapitel der Introductio. Insbesondere folgt nach dem Satz des Pythagoras dann sofort^[16]

${\displaystyle \sin ^{2}(x)+\cos ^{2}(x)=1.}$

Eine Reihe von Grundformeln der Trigonometrie wurden systematisch von Euler hergeleitet. Er benutzte die Additionstheoreme der trigonometrischen Funktionen und gab als erster einen einfachen und klaren Beweis der bekannten Formel von De Moivre. Dieser Beweis gilt auch aus heutiger Sicht als streng, falls man davon absieht, dass die vollständige Induktion formal nicht abgeschlossen wurde. Euler erhielt aus diesen Formeln die Entwicklung der trigonometrischen Funktionen in Potenzreihen, indem er dasselbe Verfahren wie im Falle der Exponentialfunktion benutzte.^[17]

Auch die Partialbruchzerlegung des Kotangens war Gegenstand von Eulers Forschung. Diese diskutierte er unter anderem in einem Brief an Christian Goldbach vom 30. Juni 1742.^[18]

Im Kontext mit seinen Studien über Funktionen einer komplexen Variablen, die teilweise von d’Alembert antizipiert wurden, gelangte Euler mittels einer schon von Johann Bernoulli verwendeten nicht-reellen Substitution zum Resultat

${\displaystyle \int _{0}^{\infty }{\frac {\sin(x)}{x}}\mathrm {d} x={\frac {\pi }{2}}.}$

In diesem Zusammenhang ist erwähnenswert, dass Euler mittels mehrfacher Anwendung des Additionstheorems ${\displaystyle \sin(x)=2\sin({\tfrac {x}{2}})\cos({\tfrac {x}{2}})}$ auf die Funktionen ${\displaystyle f_{k}(x)=\sin({\tfrac {x}{2^{k}}})}$ die Produktformel

${\displaystyle {\frac {\sin(x)}{x}}=\prod _{k=1}^{\infty }\cos \left({\frac {x}{2^{k}}}\right)=\cos \left({\frac {x}{2}}\right)\cos \left({\frac {x}{4}}\right)\cos \left({\frac {x}{8}}\right)\cdots }$

generierte.^[19]

Exponentialfunktion und Logarithmus[Bearbeiten | Quelltext bearbeiten]

Euler verwendete erstmals die Exponentialfunktion und Logarithmen in analytischen Beweisen und definierte sie erfolgreich für komplexe Zahlen. Dadurch wurde deren Anwendungsbereich stark erweitert.^[20] Damit fand er die enge Beziehung zu den trigonometrischen Funktionen. Für jede reelle Zahl ${\displaystyle \varphi }$ (im Bogenmaß) besagt die Eulersche Formel, dass die komplexe Exponentialfunktion die Gleichung

${\displaystyle \mathrm {e} ^{\mathrm {i} \varphi }=\cos(\varphi )+\mathrm {i} \sin(\varphi )}$

erfüllt. Ein spezieller Fall der obigen Formel ist als die Eulersche Identität

${\displaystyle \mathrm {e} ^{\mathrm {i} \pi }+1=0}$

bekannt. Eulers Formel zieht Beweise der Additionstheoreme und die Formel von De Moivre nach sich. So gilt zum einen

${\displaystyle (\cos(\varphi )+\mathrm {i} \sin(\varphi ))^{n}=(\mathrm {e} ^{\mathrm {i} \varphi })^{n}=\mathrm {e} ^{\mathrm {i} \varphi n}=\cos(n\varphi )+\mathrm {i} \sin(n\varphi ).}$

Auch bezüglich der Additionstheoreme bedient man sich der Multiplikativität der Exponentialfunktion. Zum anderen haben wir demnach

${\displaystyle \cos(x+y)+\mathrm {i} \sin(x+y)=\mathrm {e} ^{\mathrm {i} (x+y)}=\mathrm {e} ^{\mathrm {i} x}\mathrm {e} ^{\mathrm {i} y}=\cos(x)\cos(y)-\sin(x)\sin(y)+\mathrm {i} (\sin(x)\cos(y)+\sin(y)\cos(x)).}$

Zwei komplexe Zahlen sind genau dann gleich, wenn Real- und Imaginärteil übereinstimmen – zum Beispiel gilt also ${\displaystyle \cos(x+y)=\cos(x)\cos(y)-\sin(x)\sin(y)}$.

Integralrechnung[Bearbeiten | Quelltext bearbeiten]

In seinem Werk Institutiones calculi integralis (1768–1770), erschienen in drei Bänden, beschäftigte sich Euler mit der Integralrechnung.^[21] Darin finden sich die Methoden der unbestimmten Integration in moderner Form erschöpfend dargestellt für die Fälle, in denen die Integration auf elementare Funktionen führt. Viele Methoden sind erst von Euler entwickelt worden, und noch heute ist die Eulersche Substitution, mit deren Hilfe gewisse irrationale Differentiale rationalisiert werden können, ein Begriff.^[22] Er fand einen Weg, Integrale mit komplexen Grenzen zu berechnen, womit er wichtige Teile der Entwicklung der komplexen Analysis vorwegnahm.

Es ist zu bemerken, dass ein Vorläufer der nach Laplace benannten Laplace-Transformation bereits 1766 von Euler in seiner Institutiones calculi integralis studiert worden war.^[23] Laplace hatte sie erstmals im Rahmen der Wahrscheinlichkeitstheorie angewandt.^[24]

Fourierreihen[Bearbeiten | Quelltext bearbeiten]

Euler arbeitete auch im Bereich der Fourierreihen. Er leitete die für Werte ${\displaystyle 0<x<\pi }$ gültige Formel

${\displaystyle {\frac {\pi -x}{2}}=\sin(x)+{\frac {1}{2}}\sin(2x)+{\frac {1}{3}}\sin(3x)+{\frac {1}{4}}\sin(4x)+\dotsb }$

aus der Reihe

${\displaystyle {\frac {1-r\cos(x)}{1-2r\cos(x)+r^{2}}}-1=r\cos(x)+r^{2}\cos(2x)+r^{3}\cos(3x)+\dotsb }$

an der Stelle ${\displaystyle r=1}$ her:

${\displaystyle -{\frac {1}{2}}=\cos(x)+\cos(2x)+\cos(3x)+\dotsb }$

Obwohl die Reihe zur Rechten nirgends konvergiert, lieferte beidseitiges Integrieren, nach Wahl der richtigen Integrationskonstanten, die heute als korrekt bekannte Eulersche Reihe.^[25]

Dies ist ein typisches Beispiel der von Euler zugrunde gelegten „Allgemeinheit der Algebra“. Obwohl einige von Eulers Beweisen nach modernen Standards der mathematischen Strenge nicht akzeptabel sind,^[26] führten seine Ideen, wie eben demonstriert, zu vielen Fortschritten.

Begründung der Variationsrechnung[Bearbeiten | Quelltext bearbeiten]

Euler gilt neben Lagrange als einer der Begründer der systematischen Variationsrechnung. An verschiedene Problemstellungen und Ideen von Jakob und Johann Bernoulli anknüpfend, formulierte Euler schon seit seiner frühen Schaffensphase deren Hauptprobleme und entwickelte eine allgemeine Methode zu deren Lösung. Im Jahre 1744 erschien sein in dieser Hinsicht epochales Hauptergebnis zum Variationskalkül, die Methodus inveniendi lineas curvas. Diese Spezialdisziplin (von den Brüdern Bernoulli ansatzweise initiiert) wurde von Euler erstmals konzipiert und systematisiert. Sie beschäftigt sich mit Extremwertproblemen allgemeinster Art. Im Gegensatz zur Differentialrechnung, bei der oft lokale Maxima oder Minima von Funktionen bestimmt werden, ist die Variationsrechnung durch Probleme charakterisiert, bei denen eine oder mehrere unbekannte Funktionen derart zu bestimmen sind, dass ein gegebenes, von diesen Funktionen abhängiges bestimmtes Integral extremale Werte annimmt.^[27]

Erstmals wird in den Methodus inveniendi die Bedingungsgleichung zur Ermittlung von Extremwertaufgaben für mehrerer Kurvenscharen formuliert und gelöst. Die allgemeine Bedingung – heute bekannt und gebräuchlich als Euler-Lagrange-Gleichung – ist das Ergebnis dieser verallgemeinerten Problemstellung.

Formulierung der Aufgabe[Bearbeiten | Quelltext bearbeiten]

Die Problemstellung findet sich im Original mit den folgenden Worten:

Hierbei haben ${\displaystyle x}$ und ${\displaystyle y}$ die gewöhnliche Bedeutung von Variablen der Abszissen- und Ordinatengröße. Entscheidend ist nun die Verallgemeinerung hinsichtlich der Funktion ${\displaystyle Z}$, die hier im Einschub der Zitats ergänzt wurde. Und zwar dass die Funktion ${\displaystyle Z}$ auch hinsichtlich der abgeleiteten Größen ${\displaystyle p:=y'=dy/dx}$, ${\displaystyle q:=y''=d^{2}y/dx^{2}}$ variierbar und das Kurvenintegral ${\displaystyle \int Z\,dx}$ als ‹nicht integrierbar› gilt; denn andernfalls wäre die Kurve eines einfaches Extremwertproblem der Kurve lösbar, wie er sagt, lösbar «durch die gewöhnliche Methode der Maxima und Minima».^[29][30]

Euler beweist entsprechend zunächst folgende Aussage:

Sei ${\displaystyle Z}$ eine nach Differentialen entwickelbare Funktion der Form ${\displaystyle dZ=M\,dx+N\,dy+P\,dp+Q\,dq+\ldots }$, so dass ${\displaystyle M:=\partial Z/\partial x\,,N:=\partial Z/\partial y\,,P:=\partial Z/\partial y',\,Q:=\partial Z/\partial y'',\ldots }$; sei nun ferner ${\displaystyle Z=Z(x,y)}$ allein von ${\displaystyle x}$ und ${\displaystyle y}$ abhängig. Dann lässt sich die Variation des Funktionals ${\displaystyle Z}$ immer auf die Funktion ${\displaystyle Z(x)=y}$ zurückführen, und es gilt: ${\displaystyle N=P=\ldots =0}$.

Ferner ergibt sich die gewöhnliche Extremalbedingung der Differentialrechnung: ${\displaystyle Z'(x)={\frac {dZ}{dx}}=0}$.^[31]

Erste Variation: Begründung[Bearbeiten | Quelltext bearbeiten]

Euler schreitet nun gewissermaßen "induktiv" weiter zur so genannten Ersten Variation, bei der nach jeder infinitesimal kleinen Änderung des Kurvenverlaufs eine lineare Abhängigkeit des Funktionals ${\displaystyle Z(x,\,y,\,p)}$ von der Steigung ${\displaystyle p:=y'=dy/dx}$ angenommen wird.^[32]

Eulers Begründung ist hierbei geometrisch zu nennen: Er teilt die gedachte Kurve in verschiedene Abszissenabschnitte (siehe hier Fig. 4) ein und betrachtet die Veränderung der Funktionswerte von endlichen Nachbarpunkten, wenn ein zentraler Funktionswert in ${\displaystyle N}$ um den (infinitesimalen) Abschnitt ${\displaystyle dy=\nu \mu }$ variiert wird.^[33][34] Die Betrachtung der einzelnen Steigungsänderungen, die schließlich aufsummiert werden, führt Euler in der ersten Variation auf den ‹Differentialwert› ${\displaystyle \nu \mu (N\,dx-dP)}$. Damit die Kurve ${\displaystyle amz}$ extremal sein soll, ist dieser Differentialwert selbst Null zu setzten, so dass. in den Worten Eulers entsprechend dem lateinischen Text unter der hier angegebenen Abbildung, das zentrale Ergebnis folgt:

In heutiger Notation^[36] wird somit die Form der Euler-Lagrange-Gleichung dargestellt:

Sei das Funktional ${\displaystyle J(y)=\int _{x_{0}}^{x_{1}}f(x,y,y')\,dx}$ gegeben und ${\displaystyle f}$ eine stetige, partiell differenzierbare Funktion, so gilt für alle ${\displaystyle x\in [x_{0},x_{1}]}$:

${\displaystyle {\frac {\text{d}}{{\text{d}}x}}{\Bigl (}{\frac {\partial f}{\partial y'}}{\Bigr )}-{\frac {\partial f}{\partial y}}=0}$

Euler setzt dieses Verfahren entsprechend für Variationen von höherer Ordnung fort.^[37]

Beispielhafte Lösung der Brachistochrone[Bearbeiten | Quelltext bearbeiten]

Die Aufgabe der Brachistochrone war schon vor der Zeit Eulers ein vorrangiges mathematisches Forschungsgebiet und der ‚mechanische Anstoß‘ zur Variationsrechnung von Kurven.^[38] Sie wird von Euler nach Art einer beispielhaften Anwendung seiner Variationsmethode behandelt.^[39] Zudem ergänzt Euler sie als einen Spezialfall der Variation einer Kurvenschar

${\displaystyle \int y^{n}\,dx\,{\sqrt {1+y'^{\,2}}},{\textrm {mit}}~~n\in \mathbb {Q} ,y'=dy/dx}$.

Damit sorgt er dort für eine Verallgemeinerung der Variationsaufgabe:^[40]

Für ${\displaystyle n=-{\frac {1}{2}}}$ lautet die entsprechende Variationsgleichung^[41]

${\displaystyle \delta J[y]=\int _{a}^{b}dx\,{\frac {\sqrt {1+y'^{\,2}}}{\sqrt {y}}}=0}$, wobei das Funktional nur von ${\displaystyle y}$ abhängig ist

Der Variation entspricht die Differentialgleichung

${\displaystyle y\cdot (1+y'^{\,2})=a}$, ${\displaystyle a}$ = const., deren Lösung die Zykloidenkurve ist.^[42]

Euler löst dort auch das erste, mathematisch formulierte Variationsproblem, das von I. Newton aus dem zweiten Buch seiner Principia Mathematica stammt, in der Art eines Zusatzes (‚Lemma‘).^[43]

Im Hauptteil seiner Variationsmethode behandelt Euler die von ihm so genannten elastischen Kurvenformen, nach dem Vorschlag von Daniel Bernoulli, unter dem einheitlichen Variationsproblem des minimalen Potentials.^[44] Zur Erläuterung hat Euler einen umfangreichen Anhang (Additamentum I: De Curvis Elasticis) ergänzt. Diese Ergänzung allein begründet die mathematische Elastizitätstheorie und ging in die Wissenschaftsgeschichte ein. Er liegt in deutscher Übersetzung (von H. Linsenbarth) in der Reihe Ostwalds Klassiker vor. Der Mitherausgeber der Mechanik-Reihe der Euleri Opera Omnia Clifford Truesdell hat diesem Additamentum einen eigenen Ergänzungsband gewidmet.^[45]

Transzendente Funktionen[Bearbeiten | Quelltext bearbeiten]

Als Vorreiter auf diesem neuen Gebiet schuf Euler die Theorie der hypergeometrischen Reihen, der q-Reihen und der hyperbolischen trigonometrischen Funktionen.

Riemannsche Zeta-Funktion[Bearbeiten | Quelltext bearbeiten]

Auch die Funktionalgleichung der Riemannschen Zeta-Funktion ${\displaystyle \zeta (s)}$, die Euler für die verwandte Funktion

${\displaystyle \phi (s)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{s}}}=(1-2^{1-s})\zeta (s)}$

in der Form

${\displaystyle \pi ^{s}\left(2^{s-1}-1\right)\phi (1-s)+(2^{s}-1)\cos \left({\frac {\pi s}{2}}\right)\Gamma (s)\phi (s)=0}$

angab, sowie einige deren Werte an negativen Stellen, waren Euler bereits bekannt. Dabei handelt es sich nicht um eine klassische Gleichung, wie etwa ${\displaystyle 2x+2=0}$, die nur vom Wert ${\displaystyle x=-1}$ gelöst wird, sondern um eine Identität, d. h. die Gleichung stimmt, egal was eingesetzt wird. Beispielsweise ist ${\displaystyle x=x}$ eine (triviale) Identität, und im Falle der Zeta-Funktion stellte Euler einen für alle ${\displaystyle s}$ gültigen Zusammenhang zwischen den Werten ${\displaystyle \zeta (s)}$ und ${\displaystyle \zeta (1-s)}$ her. Diese vermutete er nach umfassenden numerischen Berechnungen, die auf der heute als richtig bekannten Darstellung

${\displaystyle (1-2^{1-s})\zeta (s)=\lim _{x\to 1^{-}}\sum _{n=1}^{\infty }(-1)^{n+1}{\frac {x^{n}}{n^{s}}}}$

beruhten.^[46] Die Riemannsche Zeta-Funktion spielt eine sehr wichtige Rolle in der Zahlentheorie und die Funktionalgleichung wurde von Bernhard Riemann, der erstmals einen strengen Beweis vorlegte, benutzt, um seine Theorie über Primzahlen aufzubauen.

Beta- und Gamma-Funktion[Bearbeiten | Quelltext bearbeiten]

Bereits im Jahr 1729 entwickelte Euler unter Hilfenahme des binomischen Lehrsatzes die für natürliche Zahlen ${\displaystyle m,n}$ gültige Formel

${\displaystyle \int _{0}^{1}x^{m}(1-x)^{n}\mathrm {d} x={\frac {1\cdot 2\cdot 3\cdots n}{(m+1)\cdot (m+2)\cdots (m+n+1)}}.}$

Daraus leitete er eine Integraldarstellung für die Fakultätsfunktion ab:

${\displaystyle n!=\int _{0}^{1}(-\log(x))^{n}\mathrm {d} x.}$

Diese Resultate führten zur Entdeckung der Beta- und Gammafunktion durch Euler, der ihre grundlegenden Eigenschaften studierte. In Korrespondenz mit Christian Goldbach im Jahr 1729 verallgemeinerte Euler zunächst die Fakultät und führte 1730 das Euler-Integral der zweiten Art ein, das für komplexe Werte ${\displaystyle z}$ mit positivem Realteil die Euler-Gammafunktion darstellt:^[47]

${\displaystyle \Gamma (z)=\int _{0}^{1}(-\log(x))^{z-1}\mathrm {d} x=\int _{0}^{\infty }t^{z-1}\mathrm {e} ^{-t}\mathrm {d} t.}$

Bereits in einem Brief von 1729 an Christian Goldbach hatte Euler eine Formel für die halbzahlige Fakultät erwähnt in der Form: ${\displaystyle ({\tfrac {1}{2}})!={\tfrac {\sqrt {\pi }}{2}}}$.^[48] Das Integral erster Art stellt die Beta-Funktion für ${\displaystyle x,y>0}$ dar:^[49]

${\displaystyle \mathrm {B} (x,y)=\int _{0}^{1}t^{x-1}(1-t)^{y-1}\mathrm {d} t.}$

Aus den besonderen Eigenschaften dieser Funktionen leitete Euler nicht nur Beziehungen zur Euler-Mascheroni-Konstanten ab, sondern gab auch die Produktformeln^[50]

${\displaystyle \Gamma (z)={\frac {1}{z}}\prod _{n=1}^{\infty }\left(1+{\frac {1}{n}}\right)^{z}\left(1+{\frac {z}{n}}\right)^{-1}}$

und

${\displaystyle {\frac {1}{\Gamma (z)\Gamma (-z)}}=-z^{2}\prod _{n=1}^{\infty }\left(1-{\frac {z^{2}}{n^{2}}}\right)=-{\frac {z}{\pi }}\sin(\pi z),}$

wobei letztere als Eulerscher Ergänzungssatz (Euler reflection formula) bekannt ist.^[51] Die Beta-Funktion ist die Grundlage der Beta-Verteilung aus der Wahrscheinlichkeitstheorie. Die Gamma-Funktion taucht bei der Gamma-Verteilung auf, spielt aber auch in Funktionen- und Zahlentheorie unter anderem im Kontext vervollständigter L-Funktionen eine wichtige Rolle.

Elliptische Integrale[Bearbeiten | Quelltext bearbeiten]

Eulers großes Interesse an elliptischen Integralen und elliptischen Funktionen geht auf seine frühen Jahre bei Johann Bernoulli zurück. Während seines Studiums an der Berliner Akademie erhielt Euler am 23. Dezember 1751 ein zweibändiges Werk von Giulio Fagnano mit dem Titel Produzioni Matematiche, das 1750 für seine formale Überprüfung veröffentlicht wurde. Diese Arbeit enthielt die Formel für die Verdoppelung der Bogenlänge der Lemniskate, deren Polarkoordinatengleichung ${\displaystyle r^{2}=a^{2}\cos(2\theta )}$, und deren algebraische Gleichung ${\displaystyle (x^{2}+y^{2})^{2}=a^{2}(x^{2}-y^{2})}$ lautet. Euler wurde durch diese Arbeit enorm inspiriert und half, einen neuen Bereich algebraischer Funktionen zu schaffen.^[52]

Euler war imstande, das heute als Additionstheorem für elliptische Integrale (erster Gattung) bekannte Resultat zu beweisen. Setzt man ${\displaystyle R(t)=1+mt^{2}+nt^{4}}$ mit ganzen Zahlen ${\displaystyle m,n}$, so folgt aus der Gleichheit

${\displaystyle \int _{0}^{x}{\frac {\mathrm {d} t}{\sqrt {R(t)}}}+\int _{0}^{y}{\frac {\mathrm {d} t}{\sqrt {R(t)}}}=\int _{0}^{z}{\frac {\mathrm {d} t}{\sqrt {R(t)}}}}$

bereits

${\displaystyle z={\frac {x{\sqrt {R(y)}}+y{\sqrt {R(x)}}}{1-nx^{2}y^{2}}}.}$

Dies wird Eulersches Additionstheorem (Euler addition theorem) genannt. Im Jahre 1753 entdeckte Euler viele Additionsformeln für elliptische Integrale, die gewöhnlich in direktem Bezug zum Additionstheorem stehen.^[53]

Zahlentheorie und Kombinatorik[Bearbeiten | Quelltext bearbeiten]

Eulers Interesse an der Zahlentheorie lässt sich auf den Einfluss von Christian Goldbach, seinem Freund in der Sankt Petersburger Akademie, zurückführen. Dabei ist Zahlentheorie im Grunde die Wissenschaft der natürlichen Zahlen ${\displaystyle 1,2,3,...}$ und deren Eigenschaften. Eine zahlentheoretische Eigenschaft einer Zahl ist dabei zum Beispiel, ob sie durch eine andere Zahl geteilt werden kann oder durch wie viele Zahlen sie geteilt werden kann. Beispielsweise hatte Euler die Einsicht, dass eine ungerade Zahl größer als ${\displaystyle 1}$ nur durch ${\displaystyle 1}$ und sich selbst teilbar ist (eine Primzahl ist), wenn es bis auf Reihenfolge nur eine Möglichkeit gibt, sie als Summe von zwei teilerfremden positiven Quadratzahlen zu schreiben. Damit ist sie gleichzeitig darstellbar als ${\displaystyle 4n+1}$ mit einer natürlichen Zahl ${\displaystyle n}$. (Gleiches gilt sinngemäß für die Quadratzahlen von Primzahlen, etwa ${\displaystyle 25=5^{2}=4\times 6+1=3^{2}+4^{2}}$). So besitzt etwa die Zahl ${\displaystyle 1\ 000\ 009}$ einen nicht-trivialen Teiler, ist also keine Primzahl, da^[54]

${\displaystyle 1\ 000\ 009=1\ 000^{2}+3^{2}=972^{2}+235^{2}.}$

Aber im Falle ${\displaystyle 29}$ gilt ${\displaystyle 29=5^{2}+2^{2}=4\times 7+1}$, die Zahlen ${\displaystyle 2}$ und ${\displaystyle 5}$ sind teilerfremd, und sonst gibt es keine weitere Möglichkeit zu einer Zerlegung in zwei nicht-triviale Quadrate. Also ist ${\displaystyle 29}$ eine Primzahl. Zu beachten ist jedoch, dass auf der anderen Seite nicht jede Primzahl als Summe zweier Quadrate geschrieben werden kann. Lediglich die Primzahlen der Form ${\displaystyle 4n+1}$ sind stets die Summe zweier Quadratzahlen. Viele von Eulers frühen Arbeiten zur Zahlentheorie basieren auf den Werken von Pierre de Fermat. Euler entwickelte einige von Fermats Ideen und widerlegte manche seiner Vermutungen.

Nach Euler sind verschiedene Zahlen und Zahlenfolgen benannt, siehe dazu Eulersche Zahlen (Begriffsklärung).

Elementare Zahlentheorie[Bearbeiten | Quelltext bearbeiten]

Zum Beispiel widerlegte er Fermats Vermutung, alle Fermat-Zahlen seien ebenfalls Primzahlen, indem er zeigte, dass die Zahl ${\displaystyle F_{5}=2^{2^{5}}+1}$ durch 641 teilbar ist.

Er trug wesentlich zur Theorie der vollkommenen Zahlen bei, die die Mathematiker seit Euklid fasziniert hatten. Euler bewies, dass die von Euklid gezeigte Beziehung zwischen (geraden) vollkommenen Zahlen und Mersenne-Primzahlen sogar eins zu eins ist, ein Ergebnis, das als Euklid-Euler-Satz bekannt ist. 1772 hatte Euler in einem Brief an Goldbach korrekt behauptet, dass ${\displaystyle 2^{31}-1=}$ 2.147.483.647 eine Mersenne-Primzahl ist.^[55] Sie galt bis 1867 als die größte gefundene Primzahl.^[56] Bereits 1732 konnte er die 19-stellige vollkommene Zahl

${\displaystyle P=2^{30}\cdot (2^{31}-1)}$

konstruieren.^[57]

Algebraische Zahlentheorie[Bearbeiten | Quelltext bearbeiten]

Er gab gleich mehrere Beweise für den kleinen Fermatschen Satz und war der erste, der einen Beweis publizierte (der von Leibniz im Jahr 1683 geführte Beweis tauchte erst 1894 auf). Sein erster Beweis wurde mittels Induktion geführt, was für die damalige Zeit ungewöhnlich war.^[58] Er führte auch die Eulersche Phi-Funktion ein. Mit Hilfe der Eigenschaften dieser Funktion verallgemeinerte er Fermats kleinen Satz zu dem, was heute als Satz von Euler bekannt ist.

Euler leistete wichtige Vorarbeit zu Lagranges Vier-Quadrate-Satz, indem er 1751 bewies, dass sich jede positive rationale Zahl als Summe vierer rationaler Quadrate schreiben lässt. Bereits zuvor, im Jahre 1748, hatte er in einem Brief an Goldbach die Identität

${\displaystyle (a_{1}^{2}+b_{1}^{2}+c_{1}^{2}+d_{1}^{2})(a_{2}^{2}+b_{2}^{2}+c_{2}^{2}+d_{2}^{2})}$

${\displaystyle {}=(a_{1}a_{2}-b_{1}b_{2}-c_{1}c_{2}-d_{1}d_{2})^{2}}$

${\displaystyle {}+{}(a_{1}b_{2}+b_{1}a_{2}+c_{1}d_{2}-d_{1}c_{2})^{2}}$

${\displaystyle {}+{}(a_{1}c_{2}-b_{1}d_{2}+c_{1}a_{2}+d_{1}b_{2})^{2}}$

${\displaystyle {}+{}(a_{1}d_{2}+b_{1}c_{2}-c_{1}b_{2}+d_{1}a_{2})^{2}}$

erwähnt, womit sich das Problem auf Primzahlen reduzieren ließ.^[59] Nachdem Lagrange gezeigt hatte, dass sich jede positive ganze Zahl als Summe vierer ganzer Quadrate schreiben lässt, lieferte Euler kurz darauf einen einfacheren Beweis.^[60] Es gilt zum Beispiel

${\displaystyle 34=5^{2}+2^{2}+2^{2}+1^{2}=25+4+4+1.}$

Bemerkenswert ist eine weitere Idee Eulers, die aus seiner Beschäftigung mit der Partitio numerorum hervorging, den Satz von Lagrange zu beweisen. Dafür betrachtete er die Potenzreihe

${\displaystyle (1+q+q^{4}+q^{9}+q^{16}+\dotsb )^{4}=\sum _{n=0}^{\infty }A_{4}(n)q^{n},}$

wobei für den Vier-Quadrate-Satz ${\displaystyle A_{4}(n)>0}$ für alle n hinreichend ist. Diese Beweisidee deutete Euler in Briefen an Goldbach und in einigen Arbeiten (wie E394, E586) an. So schrieb er im August 1750: „Dieser Weg deucht mir noch der natürlichste zu sein, um zum Beweis […] zu gelangen“.^[61] Bei der betrachteten Potenzreihe handelt es sich um die vierte Potenz einer modifizierten Thetareihe – Jacobi ging später diesen Weg um den Satz von Lagrange rein analytisch zu beweisen.

Ebenso zeigte er Fermats Satz über die Summe zweier Quadrate. Dieser liefert ein Kriterium, wann sich eine positive ganze Zahl als Summe zweier ganzer Quadrate schreiben lässt. Beispielsweise gilt ${\displaystyle 13=3^{2}+2^{2}=9+4}$, jedoch gibt es für die Zahl ${\displaystyle 7}$ keine Möglichkeit für eine solche Zerlegung.

Euler zeigte den großen Fermatschen Satz für die Fälle ${\displaystyle n=3}$ und ${\displaystyle n=4}$. Er bewies, dass keine Quadratzahl größer als Null als Summe zweier Biquadrate größer als Null geschrieben werden kann, womit bereits folgt, dass die Gleichung ${\displaystyle x^{4}+y^{4}=z^{4}}$ keine positiven ganzzahligen Lösungen besitzt. Im Fall ${\displaystyle n=3}$ faktorisierte Euler ${\displaystyle p^{2}+3q^{2}}$ zu ${\displaystyle (p+q{\sqrt {-3}})(p-q{\sqrt {-3}})}$. Durch die Verwendung dieser Variante der Gaußschen Zahlen und einer impliziten Annahme der eindeutigen Faktorisierung konnte Euler einen Beweis konstruieren, der die Unmöglichkeit des Falls ${\displaystyle n=3}$ zeigte. Wie bei seinem Beweis für den Fall ${\displaystyle n=4}$ beruhte der von Euler geführte Beweis in erster Linie auf Manipulationen algebraischer Symbole und Paritätsargumenten und führte wenig neue Methoden ein.^[62] Wie Generationen von Mathematikern nach ihm scheiterte Euler jedoch am allgemeinen Beweis des großen Fermatschen Satzes. Ein vollständiger Beweis wurde erst 1995 durch Andrew Wiles und Richard Taylor als Konsequenz des Modularitätssatzes für semi-stabile elliptische Kurven erbracht.^[63]

Euler vermutete das Gesetz der quadratischen Reziprozität, das später durch Carl Friedrich Gauß bewiesen wurde.^[64] Dabei handelt es sich um eines der grundlegendsten Konzepte der Zahlentheorie.

Kombinatorik[Bearbeiten | Quelltext bearbeiten]

Obwohl die Kombinatorik erst später zu einem neuen modernen Zweig der Mathematik wurde, haben Probleme des Zählens eine lange und frühe Geschichte. Euler betrachtete Probleme der Permutationen und Kombinationen und formulierte ein bestimmtes Problem wie folgt: Angesichts einer beliebigen Folge von ${\displaystyle n}$ Buchstaben ${\displaystyle a,b,c,d,e,\dotsc }$, wie viele Möglichkeiten gibt es, sie neu anzuordnen, sodass keine wieder auf die ursprünglich besetzte Position zurückkehrt? In diesem Zusammenhang führte Euler die Notation ${\displaystyle \Pi (n)}$ ein, um die Anzahl der Permutationen der ${\displaystyle n}$ Buchstaben ${\displaystyle a,b,c,d,e,\dotsc }$ darzustellen, bei denen keiner seine ursprüngliche Position wieder einnimmt. Eine solche Permutation wird heute als fixpunktfreie Permutation bezeichnet.

Mit einem einfachen Argument bewies Euler mehrere Rekursionsformeln für ${\displaystyle \Pi (n)}$, darunter die doppelte Rekursionsformel

${\displaystyle \Pi (n)=(n-1)\left(\Pi (n-1)+\Pi (n-2)\right).}$

Er gab auch die explizite Formel

${\displaystyle \Pi (n)=n!\left(1-{\frac {1}{1!}}+{\frac {1}{2!}}-{\frac {1}{3!}}+\dotsb +{\frac {(-1)^{n}}{n!}}\right)}$

an, die beweist, dass der Quotient aus fixpunktfreien Permutationen und allen ${\displaystyle n!}$ Permutationen rapide gegen die Zahl ${\displaystyle {\tfrac {1}{e}}\approx 0{,}367879}$ konvergiert.^[65]

Ebenfalls auf Euler geht der Pentagonalzahlensatz

${\displaystyle \prod _{n=1}^{\infty }(1-x^{n})=\sum _{n=-\infty }^{\infty }(-1)^{n}x^{n(3n-1)/2}}$

zurück, er zeigte ihn 1750.^[66] Daraus lässt sich eine Rekursionsformel für die Partitionen herleiten. Diese wurde von Percy Alexander MacMahon dazu verwendet, die Werte der Partitionsfunktion ${\displaystyle p(n)}$ bis ${\displaystyle n=200}$ zu berechnen.^[67] Dabei zählt die Funktion ${\displaystyle p(n)}$, auf wie viele Arten und Weisen sich ${\displaystyle n}$ als Summe natürlicher Zahlen schreiben lässt. Zum Beispiel ist ${\displaystyle p(4)=5}$, denn ${\displaystyle 4=3+1=2+2=2+1+1=1+1+1+1}$. Es gilt ${\displaystyle p(200)=3.972.999.029.388}$. Der Pentagonalzahlensatz ist zudem ein Eckpfeiler zwischen der Kombinatorik und der Theorie der Modulformen.

In den 1780er Jahren befasste Euler sich mit griechisch-lateinischen oder Eulerschen Quadraten, in denen in jeder Zeile und auch in jeder Spalte jedes Element einer Menge G mit n Elementen und ebenso jedes Element einer Menge L mit n Elementen genau einmal vorkommen muss, und jedes Tupel (g,l) ∈ G×L muss im gesamten n×n-Quadrat genau einmal vorkommen. Euler fand Methoden zur Konstruktion von Eulerschen Quadraten mit ungerader oder durch vier teilbarer Größe n. Es gelang ihm jedoch nicht, auch für n ≡ 2 mod 4 Lösungen zu finden. Der Fall n = 6 ist als Problem der 36 Offiziere oder 36-Offiziere-Rätsel bekannt geworden, das Euler 1779 aufgab und das keine klassische Lösung besitzt.^[68]

Analytische Zahlentheorie[Bearbeiten | Quelltext bearbeiten]

Euler verknüpfte die Natur der Primzahlverteilung mit Ideen aus der Analysis. Zum Beispiel bewies er, dass die Summe der Kehrwerte der Primzahlen divergiert. Dabei fand er die Verbindung zwischen der Riemannschen Zeta-Funktion und den Primzahlen; seine Entdeckung ist heute als Euler-Produkt-Formel für die Riemannsche Zeta-Funktion bekannt:

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{s}}}=\prod _{p\,\mathrm {Primzahl} }{\frac {1}{1-{\tfrac {1}{p^{s}}}}}={\frac {1}{\left(1-{\frac {1}{2^{s}}}\right)\left(1-{\frac {1}{3^{s}}}\right)\left(1-{\frac {1}{5^{s}}}\right)\cdots }},}$

wobei sich das Produkt über alle Primzahlen erstreckt. Wie sich später herausstellte, hat diese Identität weitreichende Konsequenzen für Aussagen über die Verteilung der Primzahlen. Eulers Arbeiten auf diesem Gebiet führten zur Entwicklung des Primzahlsatzes.^[69]

Kettenbrüche[Bearbeiten | Quelltext bearbeiten]

Auf der Grundlage früherer Arbeiten seiner Vorgänger begann Euler seine Forschungen zu Kettenbrüchen und veröffentlichte 1737 in einer Arbeit mit dem Titel De Fractionibus Continuis viele neue Ideen und Ergebnisse. Er bewies auch, dass jede rationale Zahl durch einen endlichen Kettenbruch dargestellt werden kann und fand eine unendliche Kettenbruch-Darstellung für die Zahl ${\displaystyle \mathrm {e} }$ in folgender Form:

${\displaystyle \mathrm {e} =2+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{4+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{6+\dotsb }}}}}}}}}}}}}}}}}$

Daraus (und aus einer ebenfalls unendlichen Darstellung als Kettenbruch für ${\displaystyle \mathrm {e} ^{2}}$) folgerte Euler die Irrationalität von ${\displaystyle \mathrm {e} }$ und ${\displaystyle \mathrm {e} ^{2}}$.^[70] Er gab nicht-reguläre Kettenbrüche (also ohne ausschließlich Einsen in den Zählern der neuen Brüche) für die Kreiszahl ${\displaystyle \pi }$, wie in etwa^[70]

${\displaystyle \pi =3+{\frac {1^{2}}{6+{\cfrac {3^{2}}{6+{\cfrac {5^{2}}{6+{\cfrac {7^{2}}{6+{\cfrac {9^{2}}{6+{\cfrac {11^{2}}{6+\dotsb }}}}}}}}}}}}}$

Er bewies zusätzlich ein Theorem, das besagt, dass die Lösung einer quadratischen Gleichung dann und nur dann reell ist, wenn sie eine periodische Kettenbruchentwicklung hat.^[71]

Die Euler-Mascheroni-Konstante[Bearbeiten | Quelltext bearbeiten]

Euler entdeckte 1734 (möglicherweise früher) zuerst einen Zusammenhang zwischen dem Wachstum natürlicher Logarithmen und der harmonischen Folge.^[72][73][74] Obwohl die Terme ${\displaystyle {\tfrac {1}{n}}}$ für größer werdende Werte ${\displaystyle n}$ gegen 0 streben, gilt

${\displaystyle 1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\dotsb =\infty .}$

Also ist die Summe der Kehrwerte aller natürlichen Zahlen unbeschränkt. Zieht man jedoch von der harmonischen Folge ${\displaystyle H_{N}=1+{\tfrac {1}{2}}+\dotsb +{\tfrac {1}{N}}}$ jeweils den Term ${\displaystyle \log(N)}$ ab, so wird das unbeschränkte Wachstum weggehoben und die Differenz konvergiert gegen einen Wert, der heute Euler-Mascheroni-Konstante oder Eulersche Konstante genannt wird:

${\displaystyle \gamma =\lim _{N\to \infty }\left(1+{\frac {1}{2}}+{\frac {1}{3}}+\dotsb +{\frac {1}{N}}-\log(N)\right)\approx 0{,}57721.}$

Trotz dieser fundamentalen Definition sind die algebraischen Eigenschaften von ${\displaystyle \gamma }$ bis heute weitgehend ungeklärt. Es wird vermutet, dass ${\displaystyle \gamma }$ irrational ist, jedoch wurde bisher kein Beweis dafür gefunden.^[75] Im Jahr 1736 hatte er die Zahl ${\displaystyle \gamma }$ in seiner Arbeit E47 bereits auf 15 Stellen berechnet.^[76]

Geometrie, Topologie und Graphentheorie[Bearbeiten | Quelltext bearbeiten]

Geometrie[Bearbeiten | Quelltext bearbeiten]

Die Mehrzahl seiner Entdeckungen in der Geometrie gelangen Euler durch die Anwendung algebraischer und analytischer Methoden. Das Lehrgebäude sowohl der ebenen wie auch der sphärischen Trigonometrie verdankt seine heutige Form – einschließlich der Notationsweise – Leonhard Euler. Seine – von Johann Bernoulli angeregten – Studien über geodätische Linien auf einer Fläche waren richtungsweisend für die später einsetzende Entwicklung der Differentialgeometrie. Von noch größerer Bedeutung waren seine Entdeckungen in der Flächentheorie, von der Gaspard Monge und andere Forscher in der Folge ausgehen sollten. In seinen späten Jahren schließlich nahm Euler seine Arbeiten über die allgemeine Theorie der Raumkurven exakt dort wieder auf, wo Clairaut 1731 aufgehört hatte – allerdings wurden sie erst postum gedruckt.^[77]

In den Grundlagen der Differentialgeometrie lieferte er Beiträge für die Krümmung einer Kurve und leitete eine analytische Formel für die Radien der Schmiegekreise her. Außerdem entdeckte er die zwei Hauptnormalschnitte einer Oberfläche und die Hauptkrümmungen ${\displaystyle \kappa _{1}}$ und ${\displaystyle \kappa _{2}}$. Eines seiner Ergebnisse, die sogenannte Euler-Gleichung, ergibt die Krümmung ${\displaystyle \kappa }$ eines beliebigen anderen Normalenabschnitts, der einen Winkel ${\displaystyle \alpha }$ mit einem der Abschnitte mit der Hauptkrümmung einschließt, in der Form ${\displaystyle \kappa =\kappa _{1}\cos ^{2}(\alpha )+\kappa _{2}\sin ^{2}(\alpha ).}$ Es war Euler, der sich erstmals mit abwickelbaren Oberflächen (z. B. einem Zylinder oder einem Kegel) beschäftigte, d. h. Oberflächen, die ohne Verzerrungen wie Dehnung oder Reißen in eine Ebene verformt werden können. Eine Fläche wird als Regelfläche bezeichnet (z. B. ein Zylinder, Kegel, Hyperboloid oder hyperbolisches Paraboloid), wenn sie durch die Bewegung einer geraden Linie im Raum erzeugt werden kann.^[78]

Es ist bekannt, dass Euler rein mathematisch die zuerst von Jakob Bernoulli und Christiaan Huygens studierte Kreisevolvente als günstigste Profilform der Flanken bei Zahnrädern eruiert hat. Diese Kurve liefert – sinnvoll verwendet – optimale mechanische Eigenschaften bezüglich Reibungsverlust, Geräuscharmut und Kraftübertragung (technisch realisiert wurde diese Entdeckung bzw. Erfindung Eulers erst im 19. Jahrhundert mit der Evolventenverzahnung). Weniger bekannt ist, dass Euler in dieser bereits 1762 entstandenen Arbeit E330 die heute nach Felix Savary benannte Gleichung antizipiert hat. Sie dient zur Bestimmung des Krümmungsradius einer Rollkurve und ermöglicht eine elegante Konstruktion deren Krümmungszentren.^[79]

Innerhalb der elementaren Geometrie beschäftigte sich Euler unter anderem mit einem Vorläufer des Doppelverhältnisses und den „Möndchen“ des Hippokrates. Letzteren widmete er zwei weit auseinander liegende Arbeiten E73 und E423.^[80] In einer kurzen Abhandlung E648 aus dem Jahre 1779 löste Euler das sog. Taktionsproblem des Apollonius. Dies verlangt die (elementar stets mogliche) Konstruktion eines (vierten) Kreises, der drei beliebig gegebene Kreise in der Ebene berührt. Dieses Problem wurde jedoch bereits vor Euler von François Viète, Isaac Newton und anderen gelöst. Kurz darauf verallgemeinerte er in E733 das Problem auf den dreidimensionalen Raum und fand die Konstruktion der Berührungskugel zu vier beliebig gegebenen Kugeln. Auch diese Konstruktion führt bloß auf eine quadratische Gleichung und kann somit elementar geleistet werden.^[81]

Topologie[Bearbeiten | Quelltext bearbeiten]

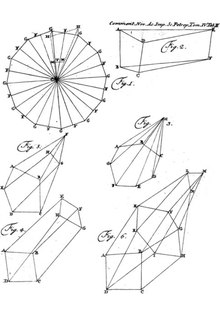
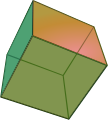
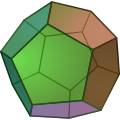
In einem Brief vom 14. November 1750 aus Berlin an Christian Goldbach nach Sankt Petersburg kündigte Euler seine Entdeckung eines fundamentalen Zusammenhangs zwischen wichtigen Größen eines konvexen Polyeders an. Seine Entdeckung war die Formel ${\displaystyle E-K+F=2}$ bezüglich Anzahl der Ecken (E), Kanten (K) und Flächen (F) eines konvexen Polyeders,^[82] eines planaren Graphen. Dieser Satz wird heute als Eulerscher Polyedersatz bezeichnet.

• 
  Wohl der prominenteste konvexe Polyeder ist der Würfel: Er hat 8 Ecken, 12 Kanten und 6 Flächen, es gilt
  8 – 12 + 6 = 2
• 
  Ein Dodekaeder hat 20 Ecken, 30 Kanten und 12 Flächen. Es gilt
  20 – 30 + 12 = 2
• 
  Ein Ikosaeder hat 12 Ecken, 30 Kanten und 20 Flächen. Es gilt, ähnlich wie links,
  12 – 30 + 20 = 2

Acht Jahre nach seinem Brief, 1758, veröffentlichte er zwei Arbeiten zu dem Thema. Die erste enthielt seine Entdeckung, die zweite einen Beweisversuch.^[82] Eulers Beweis, in dem er die untersuchten Objekte in einzelne Tetraeder zerlegen wollte, enthielt jedoch nach heutigem Maßstab an Strenge einen Fehler. Diese Lücke wurde 1924 durch Henri Lebesgue hervorgehoben.^[83]

Euler erhoffte sich mit seiner Arbeit alle Polyeder klassifizieren zu können, erreichte dieses Ziel jedoch nicht. Nach Veröffentlichung der beiden Arbeiten wandte er sich dem Thema nicht mehr zu.^[82]

Die Konstante im Eulerschen Polyedersatz wird heute als Euler-Charakteristik des Graphen (oder eines anderen mathematischen Objekts) bezeichnet und steht mit dem mathematischen Geschlecht des Objekts direkt in Zusammenhang.^[84] Der erste lückenlose Beweis des Polyedersatzes gelang erst Adrien-Marie Legendre.^[85] Die Untersuchung und Verallgemeinerung dieser Formel, insbesondere durch Cauchy^[86] und L’Huilier,^[87] markiert den Beginn der (algebraischen) Topologie.^[88][89]

Graphentheorie[Bearbeiten | Quelltext bearbeiten]

Im Jahr 1735^[90] (1741 veröffentlicht^[91] mit der Arbeit Solutio problematis ad geometriam situs pertinentis^[92]) präsentierte Euler eine Lösung für das Königsberger Brückenproblem. Die Stadt Königsberg in Preußen lag am Fluss Pregel und umfasste zwei große Inseln, die durch sieben Brücken miteinander und mit dem Festland verbunden waren. Das Problem besteht darin, zu entscheiden, ob es möglich ist, einen Weg zu wählen, der jede Brücke genau einmal überquert und zum Ausgangspunkt zurückkehrt. Das ist nicht möglich, weil zu mindestens einem Landstück eine ungerade Anzahl an Brücken führt. Diese Bedingung ist bereits durch die zur zentralen Insel führenden Brücken erfüllt. Das Brückenproblem ist gleichbedeutend mit der Frage, ob es für den der Stadtkarte entsprechenden Graphen einen Eulerkreis gibt.

Diese Lösung gilt als der erste Satz der Graphentheorie, insbesondere der planaren Graphentheorie.^[90]

Angewandte Mathematik[Bearbeiten | Quelltext bearbeiten]

Numerik und Differentialgleichungen[Bearbeiten | Quelltext bearbeiten]

Euler-Maclaurin-Formel[Bearbeiten | Quelltext bearbeiten]

Im Jahr 1732 entdeckte Euler die Formel

${\displaystyle \sum _{k=0}^{n}f(k)=\int _{0}^{n}f(t)\mathrm {d} t+{\frac {f(0)+f(n)}{2}}+\sum _{k=1}^{m}{\frac {B_{2k}}{(2k)!}}\left(f^{(2k-1)}(n)-f^{(2k-1)}(0)\right)+R_{m}}$

mit den Bernoulli-Zahlen ${\displaystyle B_{k}}$ und dem Restglied

${\displaystyle R_{m}={\frac {1}{(2m+1)!}}\int _{0}^{n}B_{2m+1}(t)f^{(2m+1)}(t)\mathrm {d} t.}$

Dabei bezeichnen ${\displaystyle B_{2m+1}(t)}$ Bernoulli-Polynome. Diese wurde unabhängig von ihm von Colin Maclaurin gefunden und trägt heute den Namen Euler-Maclaurin-Formel.^[93] Die Formel stellt einen Zusammenhang zwischen Summen ${\displaystyle f(0)+f(1)+\cdots +f(N)}$ und dem Integral ${\displaystyle \int _{0}^{N}f(x)\mathrm {d} x}$ her. Die hinteren Terme beinhalten die (höheren) Ableitungen von ${\displaystyle f}$ an den Grenzstellen und sind bei geschickter (meist nicht zu hoher) Wahl von ${\displaystyle m}$ meist schnell zu berechnen. Nützlich ist die Summenformel von Euler und Maclaurin dann, wenn die Summe sehr schwer, das Integral jedoch leicht zu berechnen ist. Zum Beispiel ist

${\displaystyle {\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots +{\frac {1}{N^{2}}}}$

schwer allgemein zu berechnen, während die Rechnung

${\displaystyle \int _{1}^{N}{\frac {1}{x^{2}}}\mathrm {d} x=\left[-{\frac {1}{x}}\right]_{1}^{N}=1-{\frac {1}{N}}}$

deutlich einfacher zu vollziehen ist (siehe auch: Integralrechnung und Stammfunktion) – zu beachten ist, dass die Summenformel auf keine bestimmten Grenzen festgelegt ist und somit auch bei 1 statt 0 beginnen kann. Beginnt man alternativ an einem großen Startwert ${\displaystyle N}$, ist somit ${\displaystyle {\tfrac {1}{N^{2}}}+{\tfrac {1}{(N+1)^{2}}}+{\tfrac {1}{(N+2)^{2}}}+\cdots }$ ungefähr gegeben durch

${\displaystyle \int _{N}^{\infty }{\frac {1}{x^{2}}}\mathrm {d} x+\lim _{M\to \infty }{\frac {{\frac {1}{N^{2}}}+{\frac {1}{M^{2}}}}{2}}+\lim _{M\to \infty }\sum _{k=1}^{m}B_{2k}\left({\frac {1}{N^{2k+1}}}-{\frac {1}{M^{2k+1}}}\right)={\frac {1}{N}}+{\frac {1}{2N^{2}}}+\sum _{k=1}^{m}{\frac {B_{2k}}{N^{2k+1}}}.}$

Andersherum kann mit der Summenformel ein (schwer zu berechnendes) Integral über diskrete Summen angenähert werden. Dementsprechend praktischen Nutzen zog Euler aus dieser Formel, um unendliche Reihen, die langsam konvergieren, schnell numerisch anzunähern. So gab er gute Näherungen für die Werte ${\displaystyle \zeta (3)}$ und ${\displaystyle \zeta (4)}$ und fand ${\displaystyle \zeta (2)}$ auf 20 Stellen genau:

${\displaystyle \zeta (2)=\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}\approx 1{,}64493406684822643647.}$

Hätte Euler stattdessen für eine solche Präzision „naiv“ die Terme ${\displaystyle {\tfrac {1}{n^{2}}}}$ summiert, wäre der Zeitaufwand mit 20 Sekunden pro Summand bei etwa 63 Billionen Jahren gelegen. Erwiesenermaßen etablierte Eulers ursprüngliche Methode der Berechnung von ${\displaystyle \zeta (n)}$ für höhere Werte von ${\displaystyle n}$ die numerische Mathematik als ein neues Forschungsgebiet.^[94]

Explizites Euler-Verfahren[Bearbeiten | Quelltext bearbeiten]

Während des siebzehnten und achtzehnten Jahrhunderts unternahmen Mathematiker ernsthafte Versuche, gewöhnliche Differentialgleichungen in Form von elementaren Funktionen und Quadraturen zu lösen. Als diese Methoden scheiterten, lösten sie Gleichungen mit Hilfe unendlicher Reihen und mit numerischen Methoden. Im Jahre 1768 entwickelte Euler ein einfaches Finite-Differenzen-Verfahren zur numerischen Lösung einer gewöhnlichen Differentialgleichung

${\displaystyle {\frac {\mathrm {d} y}{\mathrm {d} x}}=f(x,y)}$

mit der gegebenen Anfangsbedingung ${\displaystyle y(x_{0})=y_{0}}$. Mit einer einheitlichen Schrittweite ${\displaystyle h}$ zwischen den Punkten ${\displaystyle x_{0},x_{1},x_{2},\dotsc }$, konstruierte Euler die Punkte ${\displaystyle x_{n+1}=x_{0}+(n+1)h=x_{n}+h,}$ mit ${\displaystyle n=0,1,2,\dotsc }$, und erhielt dann die Formel

${\displaystyle y_{n+1}=y_{n}+hf(x_{n},y_{n})=y_{n}+hy_{n}'+O(h^{2}).}$

Hierbei bezeichnet ${\displaystyle O(h^{2})}$ die O-Notation von Landau und bedeutet in diesem Falle, dass das Fehlerrauschen jenseits ${\displaystyle y_{n}+hy_{n}'}$ im rechten Ausdruck im Wesentlichen durch die „winzige“ Zahl ${\displaystyle h^{2}}$ nicht überschritten wird. Falls ${\displaystyle f(x,y)}$ stetig ist, dann konvergiert die Folge der Euler-Polygonlinien gleichmäßig mit ${\displaystyle h\to 0}$ zu der unbekannten Funktion ${\displaystyle y(x)}$ auf einem ausreichend kleinen geschlossenen Intervall, das ${\displaystyle x_{0}}$ enthält.^[95]

Euler-Winkel[Bearbeiten | Quelltext bearbeiten]

Nach ihm sind auch die bedeutenden Euler-Winkel benannt. Es handelt sich dabei um ein Tripel aus Winkeln, mit denen die Orientierung (Drehlage) eines festen Körpers im dreidimensionalen euklidischen Raum beschrieben werden kann. Eine algebraische Beschreibung, mit der die Drehlage von beliebigen Punkten berechnet werden konnte, wurde erst ab 1775 von Euler in zunehmender Tiefe formuliert.^[96] In der ersten Arbeit zeigte er, dass die neun Elemente der Abbildungsmatrix (welche die Drehung beschreiben) wegen der Längentreue einer Bewegung nicht unabhängig voneinander sind, sondern durch nur drei voneinander unabhängige Winkel festgelegt werden, der Euler-Winkel.^[97]

In der Aerodynamik von Flugzeugen werden bis heute die Euler-Winkel verwendet. Dabei ist es Praxis, ein erdfixes Koordinatensystem zu verwenden, um die Position und Orientierung eines Flugzeugs relativ zur Erde zu beschreiben. Da es sich bei dem Koordinatensystem nicht um ein kartesisches System handelt, ergeben sich in der Regel aber einige Probleme bei der Formulierung der Flugzeugdynamik. Durch weitere Differenzierung kann dem begegnet werden. Während die Position des Flugzeugs am besten mittels eines erdfixen Koordinatensystems beschrieben werden kann, werden die Komponenten des Trägheitstensors in der Bewegungsgleichung am besten mittels eines Koordinatensystems beschrieben, welches das Gravizentrum des Flugzeugs als Ursprung hat. Die Orientierung eines Flugzeugs relativ zur Erde kann nun mit den sogenannten Euler-Winkeln beschrieben werden. Daher ist es notwendig, die Transformation zwischen den beiden oberen Koordinatensystemen mittels der drei Eulerwinkel-Drehungen abzuleiten.^[98]

Lotterien[Bearbeiten | Quelltext bearbeiten]

Euler beschäftigte sich auch mit Lotterien. 1749 trat ein italienischer Geschäftsmann namens Roccolini an Friedrich den Großen, den damaligen König von Preußen, mit dem Vorschlag heran, ein Lotteriesystem einzuführen, bei dem fünf Zahlen von 1 bis 90 gezogen werden sollten. Der König sandte den Vorschlag an seinen wissenschaftlichen Berater Euler mit der Bitte um eine mathematische Überprüfung bezüglich der Einführung einer staatlichen Lotterie in Deutschland. Auf den königlichen Wunsch hin interessierte sich Euler sehr für die Analyse der verschiedenen Aspekte des genuesischen Lotteriesystems und entwickelte ein verbessertes Lotteriesystem, nachdem er bei der Analyse dieses Glücksspiels kombinatorische Fragen angesprochen hatte. In der Folge wurde die Berliner Lotterie 1763 in Deutschland gegründet.^[99]

Im selben Jahr, in dem Preußen sein erstes Lotto veranstaltete, verlas Euler vor der Berliner Akademie eine Arbeit mit einer detaillierten und allgemeinen Analyse dieses Lottos.^[100] Eulers Arbeit wurde posthum veröffentlicht.^[101] Eines der grundlegenden Ergebnisse, die Euler erzielte, bestand darin, eine Formel für die Gewinnwahrscheinlichkeit der Wette zu finden, bei der r aus t gezogenen Zahlen bei einer Gesamtzahl von n richtig erraten werden müssen. Seine Formel lautete:

${\displaystyle \prod _{j=1}^{r}{\frac {t-j+1}{n-j+1}}}$

Anhand dieser Wahrscheinlichkeitsberechnungen berechnete Euler drei praktische Szenarien für die Auszahlungen auf alle Wetten und berücksichtigte dabei die Möglichkeit, einen Gewinn für die Lotterieveranstalter zu erzielen.^[102]

Bevölkerungswachstum[Bearbeiten | Quelltext bearbeiten]

Im Jahr 1907, fast 125 Jahre nach Eulers Tod, verwendete Alfred J. Lotka Eulers Arbeit Recherches générales sur la mortalité et la multiplication du genre humain um die Euler-Lotka-Gleichung zur Berechnung von Bevölkerungswachstumsraten abzuleiten.^[103][104] Dabei handelt es sich um eine grundlegende Methode, die in der Populationsbiologie und -ökologie bis heute verwendet wird.^[105]

Physik[Bearbeiten | Quelltext bearbeiten]

Mechanik[Bearbeiten | Quelltext bearbeiten]

Eulers Abhandlungen zur Mechanik lassen sich, entsprechend seinem „Programm“, in folgende Bereiche einteilen: Grundlagen der Mechanik (Aufbau und Struktur der Materie, Kraft und Kraftmaß, Prinzipien der Mechanik), Mechanik materieller Punkte, Mechanik starrer, Mechanik biegsamer nicht elastischer, Mechanik elastischer, Mechanik flüssiger sowie Mechanik gasförmiger Körper.^[88] In Schriften wie Mechanica, sive motus scientia analytica exposita (1736), Découverte d’un nouveau principe de mécanique (1752) und Theoria motus corporum solidorum seu rigidorum (1765) wandte Euler dabei die Mathematik auf Fragen der Physik an. Laut Clifford Truesdell „tragen in der Tat nur wenige Werke so viel zur Mechanik bei“ wie die zweit genannte Arbeit.

Punktmechanik[Bearbeiten | Quelltext bearbeiten]

Eulers Mechanikschrift von 1736^[106] ist vorwiegend der Punktmechanik gewidmet. Die Besonderheit ihres Aufbaus ist, dass im Anschluss an die mechanischen Prinzipien, die nach Newtonscher Art formuliert sind, der jeweilige Objektbereich durch algebraische Zusatzannahmen definiert wird. Die Zusatzannahmen bestimmen die Art der Kraft-Funktion ${\displaystyle F(dm,s,v)}$.

Damit kommt Euler je nach Kraftfunktion auf unterschiedliche Differentialgleichungen, die zugleich den Gegenstandsbereich definieren: Punktmassen im Raum unter Einwirkung von Zentralkräften, Berücksichtigung von weiteren Reibungskräften, periodische Bewegungsabläufe usw.

So formuliert Euler auch die differentielle Keplergleichung als Folgerung aus allgemeinen Annahmen über die Zentripetalkraft.^[107] Euler deduziert die zentrale Differentialgleichung in der damals von Johann Bernoulli und John Keill eingeführten Darstellung durch eine Fußpunktkurve (englisch pedal curve):

${\displaystyle P\,dr={\frac {h^{2}}{p^{3}}}\,dp}$.^[108]

In der heutigen Fassung entspricht das einer Phasenraum-Darstellung, bestehend aus dem Größenpaar ${\displaystyle (r,p)}$ des zentralen Radius ${\displaystyle r}$ und des tangential gerichteten Bahnimpulses ${\displaystyle p}$.^[109][110] Auf diese Weise vereinheitlicht Euler verschiedene Themengebiete der Mechanik durch algebraische oder analytische Umformulierungen.

Im zweiten Teil der Mechanica (1736) werden entsprechend Bewegungen des mathematischen Pendels untersucht, erstmals auch mit endlicher Amplitude.

Mechanik starrer Körper[Bearbeiten | Quelltext bearbeiten]

Euler bemerkte, dass die damals allgemein akzeptierten Prinzipien der Mechanik nicht ausreichten, um das Problem der Bewegung eines starren Körpers in voller Allgemeinheit zu lösen.^[111] Der Drehimpulssatz (um eine raumfeste Achse) findet sich – implizit formuliert – bereits in Eulers Manuskript von 1734 zu seiner Mechanica sowie in seiner 1738 verfassten, aber erst 1749 publizierten Scientia navalis.^[112] Zum ersten Mal hergeleitet wurde der Drehimpulssatz (bezüglicher einer raumfesten Achse) für Systeme diskreter Massenpunkte in einer Abhandlung Eulers über die Bewegung der Mondknoten, die Euler 1744 der Berliner Akademie der Wissenschaften präsentierte und 1750 publizierte.^[112] Am 3. September 1750 las er vor der Berliner Akademie ein Mémoire, in dem er das Prinzip „Kraft gleich Masse mal Beschleunigung“ im Kontext der Eulerschen Gleichung der Starrkörper-Rotation als eigene und neue Entdeckung vorstellte. Jedoch erst 1775 publizierte Euler den Drehimpulssatz in seiner allgemein gültigsten Form als unabhängiges neues mechanisches Prinzip.^[112] Aus einer Idee Johann Bernoullis in dessen Werk Hydraulica und aus der Anwendung eines Schnittprinzips an einem infinitesimal kleinen Volumenelement gewann Euler den Impulssatz der Mechanik,

${\displaystyle \mathrm {d} {\vec {K}}=\mathrm {d} m\cdot {\frac {\mathrm {d} ^{2}{\vec {x}}}{\mathrm {d} t^{2}}}}$

also das heute so geläufige „Kraft = Masse × Beschleunigung“, das auch als Grundgleichung der Translationsbewegung bekannt ist. Das Gesetz wird bis heute namentlich Newton zugeschrieben (als das 'Zweite Newtonsche Axiom'), findet sich in dieser Form dort aber nicht.^[113] Den differentiellen Charakter des Gesetzes für die drei räumlichen Dimensionen und seinen Unterschied zu den Gesetzen bei Drehbewegungen dargestellt zu haben (siehe unten den Eintrag zu „Technische Mechanik“) ist der Verdienst Eulers.^[114]

Eulerkraft

In seinem dritten, späten Hauptwerk zur Mechanik, der Theoria Motus Corporum Solidorum et Rigidorum, erstmals 1765 erschienen,^[115] entwickelt Euler einen neuartigen, elementaren Ansatz zur Begründung sämtlicher Kraftwirkungen auf ausgedehnte Körper mit starren Verbindungen, der sich von der Newtonschen Kraftdynamik für Punktmassensysteme abgrenzt. Konzeptuell entspricht Eulers Ansatz der Anwendung des Prinzips nach d’Alembert, das von der Statik eines Körpersystems ausgeht und für dynamische Einwirkungen verallgemeinert wird. Er besagt in Kurzform:

Bei jeder infinitesimalen Rotation eines Körpers um eine feste Achse, die nicht durch den Massenmittelpunkt des Körpers verläuft, wird ein dynamisches Gleichgewicht der Drehmomente auf jedes Massenelement ${\displaystyle \mathrm {d} m}$ des Körpers erzeugt. Die verlorene, kompensierende Trägheitskraft tritt dabei in Form der Eulerkraft ${\displaystyle \mathrm {d} {\vec {F}}_{\mathrm {Euler} }}$ auf, deren Betrag ${\displaystyle \mathrm {d} F_{\mathrm {Euler} }=\mathrm {d} m\cdot {\dot {\omega }}\cdot r}$ ist.^[116]

Ausgehend von dieser „elementaren“ Kraft gelingt Euler die Verallgemeinerung für beliebige starre Körper, indem er über die jeweils wirkenden statischen Flächenmomente integriert. Daran schließt sich in den darauffolgenden Kapiteln der Theoria Motus ein erstmals systematischer Stand der Mechanik starrer Körper an. Zu der damaligen Zeit gehörten vor allem folgende Bereiche dazu: der Schwerpunktsatz, der allgemeine Momentensatz, eine allgemeine Theorie der Trägheitsmomente, die Theorie des Schwingungsmittelpunktes und die Kreiseltheorie.^[117]

Eulers Verfahren, die gesamte Mechanik der starren Körper aus der Elementarkraft ${\displaystyle \mathrm {d} {\vec {F}}_{\mathrm {Euler} }}$ zu entwickeln, konnte sich in den darauffolgenden Mechanikwerken nicht durchsetzen. Schon frühzeitig etablierte sich vielmehr die Lagrangesche Fassung des d’Alembertschen Prinzips,^[118] nach der die Eulerkraft nur als abgeleitete Größe, die aus Zwangs- oder Führungskräften gebildet wird, vorkommt.^[119]

Die heutige Bezeichnung als Eulerkraft für den verallgemeinerten, vektoriellen Kraftterm ${\displaystyle {\vec {F}}_{\mathrm {Euler} }=-m\cdot {\frac {\mathrm {d} {\vec {\omega }}}{\mathrm {d} t}}\times {\vec {r}}}$ geht hingegen erst auf C. Lanczos zurück, der damit eine Bezeichnungslücke in der Mechanik schließen und Euler auf diesem Gebiet eine weitere Ehre erweisen wollte.^[120]

Strömungsmechanik[Bearbeiten | Quelltext bearbeiten]

Historisch gesehen wurden im 18. Jahrhundert von Jean d’Alembert, Daniel Bernoulli, Alexis Clairaut und Joseph Lagrange beträchtliche Fortschritte in der theoretischen Strömungsmechanik erzielt. Unter diesen großen Mathematikern leistete Euler die grundlegendsten Beiträge zur Strömungsmechanik, indem er seine berühmten Bewegungsgleichungen, die Euler-Gleichungen der Strömungsmechanik, aufstellte.

Eulers Hauptwerk auf dem Gebiet der Strömungsmechanik beruhte im Wesentlichen auf der Kontinuumshypothese und den Newtonschen Bewegungsgesetzen. Seine Arbeit bildet die Grundlage der mathematischen Theorie der Strömungsmechanik, die von seiner Entdeckung der Variationsrechnung sowie partieller Differentialgleichungen umfasst war. Er leistete grundlegende Beiträge zur Hydrostatik und Hydrodynamik in der Zeit von 1752 bis 1761 und veröffentlichte 1757 mehrere wichtige Artikel in diesen Bereichen in der Mémories de l’Academie des Sciences de Berlin. Der erste dieser Artikel befasste sich mit den grundlegenden allgemeinen Konzepten, Prinzipien und Gleichgewichtsgleichungen von Flüssigkeiten. Die zweite und die dritte Arbeit beschäftigten sich im Wesentlichen mit der Massenerhaltungsgleichung (oder der Kontinuitätsgleichung) und den nichtlinearen Euler-Bewegungsgleichungen kompressibler Flüssigkeitsströmungen. Anschließend formulierte er die Bewegungsgleichungen und die Kontinuitätsgleichung für eine nichtviskose, inkompressible Flüssigkeitsströmung mit dem ersten Beweis des berühmten d’Alembertschen Paradoxons in einer nichtviskosen Flüssigkeitsströmung, die an einem starren Körper vorbeifließt.^[121]

Außerdem arbeitete Leonhard Euler in der Mechanik auf den Gebieten der Turbinengleichung und der Kreiseltheorie, in der er neben den Eulerschen Gleichungen die Euler-Winkel einführte. Er gilt als der Entwickler der weltweit ersten Wasserturbine.^[122] Eine Rekonstruktion der Eulerschen Turbine zeigte, dass ihr Wirkungsgrad von 71 % nur wenig unter dem moderner Turbinen (Stand 2015) liegt. Auch das technisch realisierbare Prinzip des Flügelradantriebs und der Schiffsschraube ist Euler zu verdanken.^[123]

Technische Mechanik[Bearbeiten | Quelltext bearbeiten]

Die erste analytische Beschreibung der Knickung eines mit einer Druckkraft belasteten Stabes geht ebenfalls auf Euler zurück; er begründete damit die Stabilitätstheorie. Er half bei der Entwicklung der Euler-Bernoulli-Balkengleichung, die zu einem Eckpfeiler des Ingenieurwesens wurde.

Die zu den Grundlagen der Elastostatik gehörende Differentialgleichung vierter Ordnung, die in der Technischen Mechanik auch als mathematischer Ausdruck der Biegelinie bekannt ist, kann in der Form

${\displaystyle k\cdot w''''(x)=q(x)}$

bereits in der Schrift Euler (1740)^[124] gefunden werden.^[125] Dabei sind w in der Bedeutung der Durchbiegung und q in der Bedeutung einer Streckenlast (‚differentiellen Querkraft‘) bereits in Eulers Original ersichtlich, und k, das heute allgemein das Produkt ${\displaystyle k=E\cdot I}$ (Elastizitätsmodul mal Flächenmoment) bezeichnet,^[126] ist eine unbestimmte elastische Kraft.^[127]

Bemerkenswert ist, dass Euler in dieser und anderen Schriften aus der Phase seines Schaffens zwischen 1734 und 1740 Resultate zur technischen Mechanik entwickelt, die aus einer neuen und verallgemeinerten Theorie des Schwingungsmittelpunktes entstanden sind. Der Übergang zu elastischen Kontinua wird dabei als Variationsaufgabe am starren Körper verstanden und informell umgesetzt.^[128][129]

Das gilt auch für eine detaillierte Auseinandersetzung mit mechanischen Problemen zur Verbesserung von Ankerwinden, die auch aus dieser früheren Phase der Veröffentlichungen stammt. In der für ihn typischen Herangehensweise, die rein technische Fragestellung auf das Grundlegende der physikalischen Prinzipien zu bringen, nahm Euler die Preisfrage der Pariser Académie des sciences von 1737 zum Anlass, um sich der technischen Verbesserung aller Einfachen Maschinen mit Drehwirkung zuzuwenden. Die mit dem zweiten Preis ausgezeichnete Auseinandersetzung Euler (1741)^[130] umfasst gleich mehrere Neuerungen für die damalige Mechanik:

• das erste Auftreten der dynamischen Wellrad- oder Winden-Formel, einschließlich der Berücksichtigung von Reibungsverlusten.^[131]
• auf der Grundlage dieser Formel eine umfassende Behandlung der Extremwert-Kriterien der Analysis zur technischen Realisierung der besten Maße einer Ankerwinde.^[132]
• eine Beurteilung Eulers über den lückenhaften Zustand der damaligen Mechanik. Es ermangele ihr an zureichenden Prinzipien für die dynamische Beschreibung von Maschinen. Damit wandte Euler sich insbesondere momentaner Rotation in analytischen Begriffen zu.^[133]
• eine allgemeine Untersuchung von Drehmomenten und ihr Zusammenhang zu dem von Euler so genannten ‚Moment der Materie‘, welches später das Trägheitsmoment ${\displaystyle I}$ bedeuten wird. Damit verbunden tritt erstmals die Grundgleichung der Drehbewegung als betragsmäßiges Gesetz „Drehmoment = Drehbeschleunigung × Trägheitsmoment“ auf, kurz
  ${\displaystyle M=\alpha \cdot I.}$
  Die Schrift erklärt diesen Zusammenhang gleichfalls als ein neu entdecktes ‚Prinzip der Mechanik‘ und diskutiert die formal beachtliche ‚Analogie ‘ zum Grundgesetz der Translationsbewegung.^[134]
• nicht zuletzt das Bekenntnis Eulers zu einem ganzheitlichen Bild von den Wissenschaften, an deren Spitze mathematische Erkenntnisse stehen. Wenn nach Euler ein Unterschied zwischen Mathematik und ihren technischen Anwendungen bestehen würde, worauf auch manche Preisfragen der Königlichen Akademie hindeuten, so wäre dies ein künstlich hergestellter und ein für die Förderung des Zusammenhalts aller Wissenschaften unwesentlicher. Mechanik ist (nach damaligem Verständnis) angewandte Mathematik.^[135] Vielmehr sind die technischen Bereiche mit den theoretischen Methoden der Analysis und Geometrie zu verknüpfen, um in der technischen Konstruktion gesicherte Aussagen zu gewinnen. Eine technische Mechanik musste nach Eulers Verständnis zugleich auch allgemeine, mathematische Mechanik sein.

Zur letztgenannten Neuerung formuliert Euler:

Die Euler-Jacobi-Gleichung[Bearbeiten | Quelltext bearbeiten]

Für die erst noch sich in der Entstehung befindende analytische Mechanik hatte Eulers zweiter Ergänzungsteil Additatementum 2: De motu projectorum in medio non resistente^[137] besondere Beachtung unter den Mathematikern seiner Zeit und deren Nachfolgern erhalten. Denn hier hat Euler eine neue, rein analytisch zu nennende Herangehensweise an die gesamte Mechanik mitgegeben.

Mit Berufung auf die Aktionsgröße,^[138] die nach Eulers Auffassung von P. L. M. de Maupertuis in die Mechanik und in die neuzeitliche Naturphilosophie als grundlegende Größe eingeführt wurde,^[139] erklärt er dort schließlich, dass der jeweils naturgemäße Kurvenverlauf ${\displaystyle y(x)}$ stets so bestimmt ist, dass das Aktionsfunktional ${\displaystyle A[y]:=\int _{P_{1}}^{P_{2}}m\cdot v\,\cdot ds}$ zwischen den Punkten ${\displaystyle P_{1}}$ und ${\displaystyle P_{2}}$ ein Minimum bildet. Formal dargestellt heißt das:^[140]

${\displaystyle \delta A[y]=0}$.

Euler spezifiziert dort dessen Bedeutung für die Bestimmung von mechanischen Kurven, seien es nun Kurvenverläufe von Elastika oder aber Bahnkurven von punktmechanischen Projektilen, wie sie in der Ballistik behandelt werden.

Unter Berufung auf den mechanischen Energieerhaltungssatz ${\displaystyle E+U=H}$, wobei ${\displaystyle E}$ die kinetische Energie, ${\displaystyle U}$ die potenzielle Energie und ${\displaystyle H}$ die Gesamtenergie bezeichnet, fasste C. G. J. Jacobi das Prinzip später differenzierter, insofern er das Funktional zeitunabhängig über den kinetischen Anteil ${\displaystyle E}$ formulierte. Es handelt sich um die heute so genannte Euler-Jacobi-Gleichung

${\displaystyle \int _{P_{1}}^{P_{2}}{\sqrt {2m(H-U)}}\,ds}$ = Minimum.^{[141][142][143][144]}

Jacobi zeigt sich an vielen Stellen seiner Schriften beeindruckt von Eulers Pionierleistung auf diesem Gebiet der Mathematisierung der Mechanik und Physik durch das Prinzip der kleinsten Wirkung. Von ihm stammt folgende Einschätzung:

Astronomie[Bearbeiten | Quelltext bearbeiten]

Abgesehen von der erfolgreichen Anwendung seiner analytischen Werkzeuge auf Probleme der klassischen Mechanik wandte Euler diese auch in der Astronomie an – diese Arbeiten wurden im Laufe seiner Karriere durch eine Reihe von Preisen der Pariser Akademie anerkannt. Zu seinen Errungenschaften gehören die genaue Bestimmung der Bahnen von Kometen und anderen Himmelskörpern, das Verständnis der Natur von Kometen und die Berechnung der Sonnenparallaxe.^[146] Seine Berechnungen trugen zur Entwicklung präziser Längengradtabellen bei.^[147]

Nach Victor J. Katz gilt es als gesichert, dass Euler der erste Mathematiker in Europa war, der das Kalkül der trigonometrischen Funktionen systematisch durchdrang.^[148] Er tat dies in Arbeiten, die ab 1739 erschienen. Die Bedeutung der trigonometrischen Funktionen wurde ihm einige Jahre später bewusst, als er anstrebte, bestimmte Differentialgleichungen zu lösen, insbesondere lineare Differentialgleichungen mit konstanten Koeffizienten. Die im Nachhinein offensichtliche Tatsache, dass die Rechnung mit trigonometrischen Funktionen ein Schlüssel zum Verständnis „periodischer Phänomene“, einschließlich der Bewegungen von Planeten und Satelliten, ist, scheint für die Astronomen vor Euler nicht offensichtlich gewesen zu sein. Euler war der erste, der sich mit der Formulierung und Lösung des Störungsproblems beschäftigte – dem Schlüsselproblem, das formuliert und gelöst werden musste, wenn das Newtonsche Gravitationsgesetz als Grundlage für die Planeten- und Mondtheorie etabliert werden sollte.^[149]

Mit dem Kalkül der trigonometrischen Funktionen in der Hand konstruierte er eine Reihe von Mondtabellen. Diese wurden 1746 in seinem Opuscula varii argumenti veröffentlicht. Eulers erster Versuch, mit den planetarischen Störungen fertig zu werden, erfolgte als Reaktion auf den Preiswettbewerb der Pariser Akademie von 1748. Der Preis wurde ausgeschrieben für „eine Theorie von Jupiter und Saturn, die die Ungleichheiten erklärt, die diese Planeten in ihren Bewegungen gegenseitig zu verursachen scheinen, insbesondere über den Zeitpunkt ihrer Konjunktion“. Newton hatte in seiner Principia von „einer Störung der Umlaufbahn des Saturn in jeder Konjunktion dieses Planeten“ geschrieben, „die so empfindlich ist, dass die Astronomen darüber ratlos sind“.^[150] Als Reaktion auf die Ankündigung des Preisausschreibens der Pariser Akademie für 1748 schrieb Euler zwei Memoiren, die beide Mitte 1747 fertiggestellt wurden. In der ersten, die Euler der Berliner Akademie vorlegte, leitete er die Differentialgleichungen für das Problem der Störungen ab.^[151] Die zweite, eine Ableitung der Störungen des Saturn durch Jupiter, wurde im Wettbewerb eingereicht und mit dem Preis ausgezeichnet, obwohl Euler es versäumte, die scheinbare Verlangsamung des Saturn oder die Beschleunigung des Jupiter zu erklären.^[152] Eulers Preisaufsatz überzeugte mit den innovativen Methoden, die er zur Bewältigung planetarischer Störungen einführte.^[153]

Optik[Bearbeiten | Quelltext bearbeiten]

In der Optik veröffentlichte er Werke zur Wellentheorie des Lichts und zur Berechnung von optischen Linsen zur Vermeidung von Farbfehlern. Er widersprach Newtons Korpuskeltheorie des Lichts in den Opticks, die damals vorherrschend war.^[154] Seine Arbeiten zur Optik aus den 1740er Jahren trugen dazu bei, dass die von Christiaan Huygens vorgeschlagene Wellentheorie des Lichts zur vorherrschenden Denkweise wurde,^[155] zumindest bis zur Entwicklung der Quantentheorie des Lichts.^[156]

Fast die Mehrzahl von Eulers Schriften zur Optik, im ganzen sieben aus fünfzehn, sind Fragen der Dispersion gewidmet. Dabei beschäftigte ihn unter anderem wiederholt die Frage, ob Rot oder Violett die größere Frequenz hat. Euler wechselte diesbezüglich seine Ansicht dreimal, jedes Mal auf Grund einer theoretischen Betrachtung, zu der ihn ein neues Experiment, von dem er hörte, veranlasst hatte. In der Nova theoria hatte noch Rot die größte Frequenz, in zwei späteren Arbeiten korrigierte er diese Ansicht unter anderem auf Grund seiner Theorie der Beobachtungen von Farben dünner Schichten. Dann aber wird er durch eine Betrachtung über die Elastizität von Metalllamellen wiederum auf die erste, falsche Ansicht zurückgeführt, um dann schließlich zur richtigen zurückzukehren.^[157]

Ballistik[Bearbeiten | Quelltext bearbeiten]

1745 übersetzte Euler das Werk New principles of gunnery des Engländers Benjamin Robins ins Deutsche. Es erschien im selben Jahr in Berlin unter dem Titel Neue Grundsätze der Artillerie enthaltend die Bestimmung der Gewalt des Pulvers nebst einer Untersuchung über den Unterscheid(sic) des Wiederstands(sic) der Luft in schnellen und langsamen Bewegungen.^[158] Seit Galilei hatten die Artilleristen die Flugbahnen der Geschosse als Parabeln angesehen, wobei sie den Luftwiderstand für vernachlässigbar hielten. Robins hat als einer der ersten Experimente zur Ballistik ausgeführt und gezeigt, dass die Flugbahn durch den Luftwiderstand wesentlich beeinflusst wird. Somit wurde dank Robins und mit Eulers Hilfe „das erste Lehrbuch der Ballistik“ geschaffen. Es wurde zum Beispiel in Frankreich (in französischer Übersetzung) als offizielles Lehrbuch in den Militärschulen eingeführt. Napoleon Bonaparte musste es als Leutnant studieren.^[159]

Schiffbau[Bearbeiten | Quelltext bearbeiten]

Weniger bekannt sind Eulers Arbeiten zum Stabilitätskriterium von Schiffen, in denen er das bereits erworbene, aber wieder verlorengegangene Wissen von Archimedes erneuerte.^[160] Die Scientia navalis, das bis weit ins 19. Jahrhundert vorgreifende Hauptwerk über das Schiffsingenieurwesen, erschien während der ersten Berliner Jahre.^[161]

Der erste Band definiert allgemeine Prinzipien der Hydrostatik und errichtet die erste Theorie der Trägheitsmomente ausgedehnter Körper, auf deren Grundlage das Stabilitätskriterium für Schiffsschwingungen analysiert wird. Im Ergebnis stimmen Eulers Ansatz über so genannte „rückführende Momente“, ${\displaystyle |{\vec {M}}|=h|{\vec {F}}_{G}|\cdot \sin \theta ,}$^[162] und Bougers Ansatz über die Schwingung um das so genannte Metazentrum überein.^[163]

Algebra[Bearbeiten | Quelltext bearbeiten]

In der Algebra beschäftigte sich Euler unter anderem mit der expliziten Gestalt von Einheitswurzeln. Diese treten als Lösungen der Gleichungen ${\displaystyle x^{n}-1=0}$ auf. Im 18. Jahrhundert galt es als wegweisende Problemstellung, die Lösungen dieser Gleichungen algebraisch geschlossen durch „Radikale“ auszudrücken. Auch Euler hatte in diesem Bereich Erfolge und löste die Einheitsgleichungen bis ${\displaystyle n\leq 10}$. Als technisch besonders schwierig gilt hierbei das Verfahren für ${\displaystyle x^{7}-1=0}$, das die Lösungen in Termen von Quadrat- und Kubikwurzeln ausdrückt.^[164]

Euler studierte intensiv Diophantische Gleichungen der Form ${\displaystyle y^{2}=ax^{3}+b^{2}}$ und ${\displaystyle y^{2}=ax^{2}+bx+c}$, wobei ${\displaystyle a,b,c}$ ganzzahlig sind und ${\displaystyle a>0}$ keine Quadratzahl ist. In größerer Allgemeinheit untersuchte er Gleichungen des Typs

${\displaystyle Ax^{2}+2Bxy+Cy^{2}+Dx+Ey+F=0,}$

bei denen die Diskriminante ${\displaystyle \Delta =B^{2}-AC>0}$ keine Quadratzahl ist.^[165]

Euler arbeitete Näherungsmethoden für die Lösung numerischer Gleichungen aus und bearbeitete ferner – wahrscheinlich von Daniel Bernoulli angeregt – das Eliminationsproblem. So gelang ihm ein Beweis des bereits Newton bekannten Satzes, dass zwei algebraische Kurven vom Grad m bzw. n höchstens mn Schnittpunkte haben können. In diesem Zusammenhang gelangte er zum wichtigen Begriff der Resultante. In den beiden Abhandlungen E147 und E148 vom Jahre 1750 gab Euler eine stichhaltige Erklärung des sogenannten Cramerschen Paradoxons.^[166]

1770 brachte er das Buch Vollständige Anleitung zur Algebra heraus. Er erarbeitete eine Methode zur Lösung von quartischen Gleichungen. Euler bemerkte ebenfalls, dass sich quintische Gleichungen im Allgemeinen nicht mehr durch Radikale (also geschlossene Verkettungen von Wurzelausdrücken) auflösen lassen. Dieses Resultat wurde jedoch erst später durch Niels Henrik Abel und Évariste Galois bewiesen.^[167]

Logik[Bearbeiten | Quelltext bearbeiten]

Euler wird auch die Verwendung geschlossener Kurven zur Veranschaulichung der syllogistischen Argumentation zugeschrieben. Diese Diagramme sind als Euler-Diagramme bekannt geworden. In den Briefen 101 bis 108 (an eine deutsche Prinzessin), die im Februar und März 1761 verfasst wurden, werden die heute als Venn-Diagramme bezeichneten Diagramme vorgestellt, obwohl das eine falsche Bezeichnung ist. Diagramme für mathematische Darstellungen in der Logik tauchten in einigen Abhandlungen des achtzehnten Jahrhunderts zu diesem Thema auf, und es ist möglich, dass Johann Heinrich Lambert sie kurz vor Eulers Briefen verwendete. In den Briefen 101 und 102 betonte Euler die Notwendigkeit einer disziplinierten Sprache bei der Darstellung allgemeiner Ideen und ihrer Erweiterung; er verwendete Kreise in Diagrammen, um verschiedene Formen von Syllogismen und hypothetischen Propositionen zu erklären.^[168]

Ein Euler-Diagramm ist ein diagrammatisches Mittel zur Darstellung von Mengen und ihren Beziehungen. Euler-Diagramme bestehen aus einfachen geschlossenen Kurven (normalerweise Kreisen oder auch Ellipsen) in der Ebene, die jeweils Mengen darstellen. Jede Eulerkurve teilt die Ebene in zwei Bereiche oder „Zonen“: den inneren Bereich, der symbolisch die Elemente der Menge einschließt und darstellt, und den äußeren Bereich, der alle Elemente darstellt, die nicht zur Menge gehören (Komplement). Die Größen oder Formen der Kurven spielen dabei keine Rolle. Das Diagramm soll lediglich veranschaulichen, wie sie sich überlappen. Die räumlichen Beziehungen zwischen den von jeder Kurve begrenzten Bereichen (Überlappung, Eingrenzung oder keines von beiden) entsprechen mengentheoretischen Beziehungen (Schnittmenge, Teilmenge und Disjunktheit). Kurven, deren innere Zonen sich nicht schneiden, stellen disjunkte Mengen dar. Zwei Kurven, deren innere Zonen sich schneiden, repräsentieren Mengen, die gemeinsame Elemente haben (nicht-leere Schnittmenge): Die Zone innerhalb beider Kurven stellt dabei die Menge der Elemente dar, die beiden Mengen gemeinsam sind. Eine Kurve, die vollständig im Bereich einer anderen enthalten ist, stellt eine Teilmenge dieser dar.

Euler-Diagramme (und die allgemeineren Venn-Diagramme) wurden ab den 1960er Jahren im Zuge der Neuen Mathematik als Teil des Unterrichts in der Mengenlehre aufgenommen.

Kartographie und Geodäsie[Bearbeiten | Quelltext bearbeiten]

Großes Interesse legte Euler für astronomisch-geodätische und kartographische Fragen an den Tag, für deren Lösung bei der Petersburger Akademie der Wissenschaften auf Joseph-Nicolas Delisles Anregung eine neue wissenschaftliche Institution ins Leben gerufen wurde – das sogenannte Geographische Departement. Euler war dort als Delisles Helfer eine Reihe von Jahren tätig. Der Einblick in verschiedene Dokumente dieses Departements, vor allem in die Protokolle, brachte viele Einzelheiten über Eulers Tätigkeit auf dem Gebiet der Geodäsie und Kartographie zutage. So konnte z. B. festgestellt werden, dass Eulers Anstellung im Geographischen Departement durchaus seinen Wünschen und wissenschaftlichen Neigungen entsprach. Eulers erste Arbeit war die vom Senat angeforderte Karte von Russlands europäischen Grenzen. Am 2. September beriet sich Euler mit Delisle darüber, wie eine solche Karte am besten zu konstruieren sei. Euler beendete die Karte der europäischen Grenzen Russlands am 6. September 1736. Erst am 14. Oktober 1736 war die von Euler und Delisle gemeinsam begonnene Karte, nach Korrekturen des Adjunkten Wassili Jewdokimowitsch Adodurow, endgültig fertiggestellt.^[169]

Mathematische Musiktheorie[Bearbeiten | Quelltext bearbeiten]

Auch im Bereich der Musik beruhten Eulers Gedanken hauptsächlich auf der Mathematik: Er begründete eine auf mathematischen Gesetzen aufbauende Musiktheorie (unter anderem Tentamen novae theoriae musicae, 1739, Music mathématique, Paris 1865).^[170] Sein Modell des Tonnetzes wird noch heute bei Berechnungen zur reinen Stimmung verwendet. Obwohl seine Schriften über Musiktheorie nur einen kleinen Teil seiner Arbeit ausmachen (einige hundert Seiten, bei einer Gesamtproduktion von etwa dreißigtausend Seiten), spiegeln sie dennoch ein bereits früh gewecktes Interesse wider, das ihn sein ganzes Leben lang nicht mehr verlassen hat.^[171]

Zum Verständnis von Eulers Musiktheorie muss bekannt sein, dass musikalische Intervalle in der sog. reinen Stimmung mit den Tonstufen Oktave, Quinte, Quarte und große Terz entsprechend den Frequenzverhältnissen 1:2, 2:3, 3:4 bzw. 4:5 zum Grundton aufgebaut werden. Im Gegensatz dazu steht die heute meist gebräuchliche gleichstufige Stimmung (wohltemperiert), bei der zwei Töne eines Halbtons stets das exakte Frequenzverhältnis ${\displaystyle {\sqrt[{12}]{2}}\approx 1,059463}$ haben.

Der Musikwissenschaftler Martin Vogel stellt fest: „Eine durchaus brauchbare und für die Praxis geeignete Konsonanzgradberechnung wurde von Leonhard Euler aufgestellt.“ Er fährt fort, „daß ihre Ergebnisse mit den tonpsychologischen Testen weitgehend übereinstimmen. Für die praktische Arbeit des Komponierens und des Analysierens lassen sich aus ihr wichtige Folgerungen gewinnen“.^[172] „Euler geht davon aus, daß der Mensch in einer geordneten Welt leben will und daß das nicht gar zu anstrengende Erfassen dieser Ordnung sein Wohlbefinden steigert. … Euler folgerte weiter: Je einfacher ein Verhältnis^[173] sei, durch je kleinere Zahlen es ausgedrückt werde, desto deutlicher könne es wahrgenommen werden und desto angenehmer sei seine Wirkung.“^[174] Euler versucht nun, diese Einfachheit genauer zu definieren und so in mathematische Formeln zu fassen, dass es dem Höreindruck möglichst gut entspricht. Dabei verwendet er Primzahltheorien.

Zunächst definiert Euler für Konsonanzen, d. h. Zusammenklänge, einen „Grad“. Dieser soll die „Schwierigkeit“ eines Zusammenklangs von Tönen mathematisch erfassen. Ein niedriger Grad spricht dabei für einen „annehmlichen“ – ein hoher Grad für einen „unannehmlichen“ Klang. Als Funktion verwendete Euler den Gradus suavitatis („Grad der Lieblichkeit, der Verträglichkeit“) ${\displaystyle \Gamma (n)}$, der rein abstrakt als eine zahlentheoretische Funktion interpretiert werden kann: Für eine natürliche Zahl n mit Primfaktorzerlegung ${\displaystyle n=p_{1}^{a_{1}}\cdots p_{r}^{a_{r}}}$ ist er definiert durch

${\displaystyle \Gamma (n)=1+\sum _{j=1}^{r}a_{j}(p_{j}-1).}$

Der Gradus suavitatis stellt somit eine Bewertung der Primfaktorzerlegung natürlicher Zahlen dar und ist umso größer, je größer die auftretenden Primzahlen und je größer deren Exponenten sind.^[175] Zweiklänge werden nun wie folgt gradiert: Für das Verhältnis a:b, wobei bereits vollständig gekürzt wurde, d. h., a und b sind teilerfremd, setzt man

${\displaystyle \Gamma (a:b):=\Gamma (a\cdot b).}$

Euler nennt die Zahl ${\displaystyle a\cdot b}$